госы / Шпоры - 2

2.5. Классификация кривых второго порядка

Кривой второго порядка называется ГМТ плоскости, координаты которых в некоторой ПДСК удовлетворяют уравнению второй степени вида

(8)

Конические сечения (эллипс, гипербола, парабола) являются кривыми второго порядка (следует из вида их канонических уравнений).

Преобразуем уравнение (8). Докажем, что за счет поворота осей координат можно добиться отсутствия произведения. Формулы поворота имеют вид:

В уравнение (8)вместо и подставим их значения:

.

Это уравнение представим в виде (8):

(9)

Отсюда имеем: ;

.

Это уравнение всегда имеет решение, т. е. существует такой угол , что в новой системе координат .

Будем рассматривать уравнение (9) в новой системе координат, полученной из исходной поворотом на угол .Тогда уравнение (9) имеет вид:

(10)

Возможны два случая: а) оба коэффициента и отличны от нуля;б) один из этих коэффициентов равен 0, пусть (вариант невозможен, так как при переходе из одной системы координат в другую степень уравнения не меняется).

Рассмотрим первый случай (а).

Уравнение (9) представим в виде:

(11)

Перенесем начало координат в точку ,т. е. перейдем к новой

системе ,которая относительно системы задается формулами

; . В системе координат уравнение (11) имеет вид

.(12)

Возможны следующие варианты:

а₁) , знакиисовпадают, но противоположны знаку с.

Тогда(12).(13)

Введя обозначения , , получим, что в системе уравнение (9) имеет вид:

3. Математический анализ

3.1. Предел и непрерывность функции одной переменной

Определение. Число A называется пределом функции y=f(x) в точке x₀, если для любого положительного числа  можно найти такое положительное число , что для всех x, удовлетворяющих условию

0<x–x₀<,

выполняется условие

y–A<.

Тот факт, что A есть предел функции y=f(x) в точке x=x₀, записывается формулой

.

Важно знать и о понятиях предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f(x), определенную на полубесконечном промежутке (х₀;).

Определение. ЧислоА называется пределом функции f(x) при х, стремящемся к бесконечности:,

если для любого положительного числа  можно найти такое положительное число M(зависящее от), что для всех чисел х, превосходящих М, выполняется условие:f(x) – A<.

Пусть теперь функция f(x) определена на полубесконечном промежутке (–; х₀).

Определение. ЧислоА называется пределом функции f(x) при х, стремящемся к минус бесконечности: ,

если для любого положительного числа  можно найти такое положительное число M(зависящее от), что для всех чисел х, меньших, чем –М, выполняется условие:f(x) – A<.

Определение. Функция y=f(x) называется непрерывной в точке x=x₀, если она определена в этой точке и ее значение f(x₀) равно пределу функции в этой точке: .

Определение. Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.

Приведем свойства предела функции (без доказательства).

1. Функция не может иметь в одной точке два разных предела.

2. , если C—постоянная функция.

3. Если существует и C — постоянная функция, то

.

4.Если существуюти , то существует , равный

, а также существует , равный .

Если при этом , то существует, равный.

Рассмотрим определения так называемых “односторонних пределов”.

Определение. Число B называется пределом функции f(x) в точке a справа (записывается в виде формулы ), если для любого положительного числа  найдется положительное число , такое что из условия0<x–a<будет следовать

B–f(x)<.

Согласно приведенному определению. Отметим, что обыкновенного предела функция в точке x=0 не имеет.

Определение. ЧислоС называется пределом функции f(x) в точке b слева

( записывается в виде формулы ), если для любого положительного числа  найдется положительное число  такое, что изусловия0<b–x<будет следовать C–f(x)<.

3.2. Определённый интеграл и его свойства

Понятие определённого интеграла является одним из основных понятий математического анализа. Рассмотримнепрерывную на функцию .Разобьём отрезокна n – частей точками . В результате получим , длины которых обозначим через , где . На каждом из полученных отрезков произвольно выберем точки в каждой точке вычислим значение заданной функции . Составим сумму произведений т.е. которая называется интегральной суммой для функции на . Рассматривая различные разбиения отрезка , при которых мы получим последовательность интегральных сумм.

Определение. Если при любых разбиениях отрезка таких, что ,и при любом выборе точек на отрезках интегральные суммы стремятся к одному и тому же пределу, то этот предел называется определённыминтеграломотфункциинаотрезкеиобозначается т.е.

где а иb – соответственнонижний иверхний пределы интеграла, х – переменная интегрирования, – подынтегральная функция, – подынтегральное выражение.

Определение. Если для функции существует предел то функцию называют интегрируемой на отрезке .

Теорема. Если функция непрерывна на отрезке, то она интегрируемана этом отрезке.

Доказательство.Рассмотрим нижнюю и верхнюю интегральные суммы для непрерывной функции на при произвольном разбиении отрезка : где – наименьшее значение функции на отрезке , – наибольшее значение функции на отрезке . Запишем разность верхней и нижней интегральных сумм: .

Введем обозначение для наибольшей из разностей при данном разбиении, положив , тогда разность верхней и нижней интегральных сумм запишется в виде

.

Согласно свойству равномерной непрерывности функции, непрерывной на замкнутом множестве, т. е. для непрерывной функции

на при любом способе разбиения отрезка и при имеет место

,то получим, т. е. или,

гдеи.

Учитывая, что для любого разбиения отрезка имеет место соотношение , где , ипереходя к пределу в этом соотношении при , получимили, т.е. или.

По определению определенного интеграла имеем

3.3. Производная определенного интеграла по его верхнему пределу.Формула Ньютона – Лейбница

Теорема.Если непрерывна на отрезке, то производнаяопределенного интеграла по его верхнему пределу равна подынтегральнойфункции, в которую вместо переменной интегрирования подставлено значение верхнего предела.

Доказательство. Рассмотрим определенный интеграл, у которого его верхний предел является переменной, тогда этот интеграл есть функция верхнего предела, которую обозначим через , т. е. . Докажем, что . Найдем производную этой функции. Учитывая определение определенного интеграла и его свойства,имеем:

.

Теорема. Если непрерывна на отрезке и – любая её первообразная на этом отрезке, то имеет место равенство .

Доказательство. Рассмотрим произвольную первообразную Ф(х)функции.Из доказанной теоремы следует, что непрерывная функция на отрезке имеет первообразную функцию х)+С

. Учитывая, что две первообразные данной функции отличаются на постоянное слагаемое, получим: – Ф(х)=С. Запишем это соотношение в виде= Ф(или . Для определения постоянной С положим в записанном соотношении их=а, тогда или 0=Ф(а)+С, откуда получим С= –-Ф(а). Подставляя полученное значение С в наше соотношение , получим , которое при запишется в виде:.Полученная формула называется формулой Ньютона-Лейбница. Формула Ньютона – Лейбница (или основная формула интегрального исчисления) даёт эффективное и простое средство для вычисления определённого интеграла.

Пример. Вычислите интеграл.

Решение. Воспользуемся методом интегрирования по частям, т. е.формулой .

3.4. Вычисление площади плоской фигуры при помощи определенного интеграла

Рассмотрим площадь криволинейной трапеции, ограниченной прямыми x=a, x=b, участком оси абсцисс и графиком непрерывной на функции , где . Разобьём на n произвольных частей точками , где x₀ совпадает с a, x_nсовпадает с b.На каждом полученном в результате разбиения сегменте выберем произвольные точкигде i=0,…, n-1; вычислим значения функции в точках , т.е. ; длины полученных сегментов обозначим через . Тогда произведение вида даёт нам площадь прямоугольника с основанием и высотой . Если просуммировать произведения по всем iот 0доn-1, то даёт нам площадь некоторой ступенчатой фигуры, состоящей из прямоугольников, которая может дать нам приближённое значение искомой площади, которую обозначим через S, т.е.

.

Переходя к пределу в этом соотношениипри, получим

площадь искомой фигуры .

В случае если на, то, тогда

искомая площадь вычисляется по формуле.

Пусть требуется вычислить площадь криволинейной трапеции, ограниченной линией, заданной параметрическими уравнениями:

где , то можно воспользоваться формулой

.

Пусть требуется вычислить площадь криволинейного сектора в полярных координатах, т.е. требуется определить площадь сектора, ограниченного кривой и радиус-векторами , то площадь искомого криволинейного сектора можно определить следующим образом.

Разобьём область на nчастей радиус-векторами,где ,где совпадает с, а совпадает с .

Обозначим через , где, возьмём произвольным образом вычислим и заменим каждый криволинейный сектор, полученный в результате его разбиения на n частей, круговым сектором с радиусом и центральным углом , площадь, которого равна

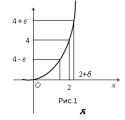
Определение. Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если

().

Например, функция непрерывна справа в точке x=0.

Определение. Функция называется непрерывной на замкнутом промежутке

[a, b], если она непрерывна на открытом промежутке (a,b), непрерывна справа в точке a и непрерывна слева в точке b.

Теорема. Для того чтобы выполнялось равенство , необходимо и достаточно, чтобы одновременно выполнялись два равенства:; Примеры. 1. Рассмотрим функцию y=x² в точке . Значение функции в этой точке равно 4. Отметим одну особенность поведения функции вэтой точке.

Можно выбрать какое-либо положительное число и построить -окрестность точки y₀=4. Очевидно, что найдется такая окрестность точки x₀=2 (на рисунке 1 эта окрестность имеет радиус ), что если x будет лежать в этой окрестности, то соответствующее значение y, равное x², попадет в -окрестность точки y₀=4. Это заключение справедливо для любого, сколь угодно малого числа. Здесь точка x₀=2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение. 2. Рассмотрим функцию . Эта функция не определена в точке x₀=2. При x₀2 её можно преобразовать: . График функции представлен

на рисунке 2. Хотя исходная функция не определена в точке x₀=2 и естественно не равна 3 в этой точке, точка y₀=3 имеет характерную особенность. Выбрав положительное число , можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x₀=2 (или лежащие в некоторой окрестности точки x₀=2, причем радиус этой окрестности зависит от), то соответствующие значения y попадут в – окрестность точки y₀=3. Замечание. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Рассмотрим основные свойства непрерывных функций.

1. Если функция f непрерывна на некотором отрезке , то внутри этого отрезка найдется, по крайней мере, одна точка такая, что значение функции в этой точке будет удовлетворять соотношению , гдех – любая другая точка отрезка, и найдется по крайней мере одна точка такая, что значение функции в этой точке будет удовлетворять соотношению.

2. Пусть функция fнепрерывна на отрезке и на конце этого отрезка принимает значения разных знаков, тогда между точками а и bнайдется, по крайней мере, одна точка с, в которой функция обращается в нуль: .

3. Пусть функцияfопределена и непрерывна на отрезке . Если на концах этого отрезка функция принимает неравные значения , , то каково бы ни было число , заключенное между числамиА и В, найдется такая точка с, заключенная между а и b, что.

Если функцияf при х = а имеет разрыв, то для выяснения характера разрыва следует найти предел функции f справа и слева. В зависимости от характера поведения функции в окрестности точки разрыва различают два основных вида разрывов:

• разрыв первого рода – в этом случае существуют конечные пределы и ; разрыв второго рода – в этом случае и(или)

не существует или бесконечен.

– эллипс. Отсюда следует, что уравнение (9) есть уравнение эллипса. а₂) , знаки ,, ссовпадают. В уравнении (13) обе части умножаем на– 1, тогда получиммнимый эллипс:.

₃) , знаки ипротивоположны. Пусть для определенности , . Тогда (13)– гипербола с действительной осью .

Если же , , то получим снова гиперболу (сопряженную прежней). Итак, и в этом случае (9) — уравнение гиперболы.

а₄) с = 0, знаки иразличны. Пусть , ;

(12)—пара пересекающихся прямых.

а₅) с = 0, знаки иодинаковы, (12) — пара мнимых прямых, пересекающихся в действительной точке. Рассмотрим теперь второй случай (б). Уравнение (9) в новой системе координат имеет вид: (14)

Возможны варианты: б₁) .

(14).

Замена переменных:

; .

В новой системе координат последнее уравнение имеет

вид: — уравнение параболы.

б₂) . Уравнение (14) имеет вид:. Замена переменных: , . Тогда имеем: , , где. Исследуем полученное уравнение :

— пара параллельных прямых;

— пара совпадающих прямых. Итак, получили следующую классификацию кривых второго порядка. Вещественная кривая второго порядка есть либо коническое сечение, либо пара прямых. Число всех кривых второго порядка равно 9.

.

1. Если – интегрируемая функция на отрезке, то она является интегрируемой и на отрезке , причём .

2. При любом расположении точек a,bи с,если интегрируемая функция в наибольшем из отрезков, и , то имеет место равенство .

3. Если и –интегрируемые функции на отрезке , то их сумма и разность также интегрируемые функции на отрезке , причём: .

4. Если – интегрируемая функция на отрезке, неотрицательна и то

5. Если и –интегрируемые функции на отрезке и удовлетворяют

неравенству (или ), то

(или ), где .

6. Если – интегрируемая функция переменного знака на отрезке и , то .

7. Если –интегрируемая функция на отрезке и при всех имеет место соотношение гдеm – наименьшее значение функции на отрезке , M – наибольшее значение функции на отрезке и то выполняется следующее соотношение: .

8. Теорема о среднем значении. Пусть –интегрируемая функция на отрезке и при всех имеет место соотношение тогда

где

Тогда площадь искомого криволинейного сектора приближённо может быть представлена суммой таких круговых секторов, т.е.

.

Переходя в последнем соотношении к пределу при получим

или.

Пример.Вычислите площадь, ограниченную кардиоидой

.

Решение. Учитывая симметрию кардиоиды относительно полярной оси,получимудвоенную площадь при изменении от 0 до , тогда по приведенной выше формуле получим искомую площадь, ограниченную данной кардиоидой:

Полагая в данном интеграле, найдем =и. Тогда по указанной формуле получим: