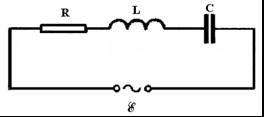
- •Ответы на вопросы к экзамену
- •1. Как определить взаимные проводимости (расчетным и экспериментальным путем)?
- •2. В чем заключается принцип линейности? Как определить соответствующие коэффициенты.
- •3. Как определить для разветвленной цепи опытным путём параметры эквивалентного генератора?
- •4. Условие получения максимума мощности в сопротивлении.
- •5. В электротехнике принято фазовое определение резонанса. Как это понимать?
- •6. Как определяется добротность контура?
- •7. Какие величины равны друг другу при резонансе?
- •9. Дать определение резонанса токов. Какие величины равны друг другу при резонансе?
- •10. Может ли ток в одной из ветвей цепи переменного тока быть больше чем суммарный ток? Пояснить с помощью 1 закона Кирхгофа.
- •11. Как экспериментально определяется коэффициент взаимной индукции?
- •7.1. Определение взаимной индуктивности
- •12.Как экспериментально определяются одноимённые концы индуктивно-связанных катушек?
- •13. Как рассчитать коэффициент индуктивной связи?
- •14. Как экспериментально определить индуктивность реле обмотки?
- •15. Как проводится «развязка» индуктивно связанных обмоток?
- •16. Нарисуйте схему замещения трансформатор без индуктивных связей.
- •17. Что такое «вносимое сопротивление». Отчего оно зависит?
- •18. В схеме звезда с нейтральным проводом был симметричный режим и вдруг произошел обрыв фазного провода. Назовите, что изменилось и в какую сторону.
- •19. В схеме звезда без нейтрального провода был симметричный режим и вдруг произошел обрыв фазного провода. Назовите, что изменилось и в какую сторону.
- •20. В схеме звезда с нейтральным проводом был симметричный режим и вдруг произошло короткое замыкание нагрузки в фазе а. Назовите, что изменилось и в какую сторону.
- •21. При каких условиях можно вести расчет трехфазной цепи «на одну фазу».
- •22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник.
- •23. Как определяется мощность в трёхфазных цепях?.
- •24. Как изменятся фазные токи при обрыве фазного провода?
- •25. Как изменятся линейные токи при обрыве фазного провода?
- •26. Как изменятся фазные токи при обрыве линейного провода?
- •27. Как изменятся линейные токи при обрыве линейного провода?
- •28. Что называется критическим сопротивлением?
- •29. Что такое декремент затухания? Как он определяется?
- •30. Как связаны друг с другом ток и напряжение на конденсаторе?
- •31. Как связаны друг с другом ток и напряжение на индуктивности?
- •32. Сформулируйте законы коммутации
- •14.2. Законы (правила) коммутации
- •35. Нарисовать график тока в цепи rlc при подключении под постоянное напряжение, если корни характеристического уравнения вещественные.
- •41. Что такое передаточная функция цепи и как ее найти?
- •42. Как связаны переходные и импульсные характеристики с передаточной функцией цепи?
- •43. Как строится вольт-амперная характеристика двух нелинейных элементов, включенных последовательно, параллельно, при смешанном соединении нескольких нелинейных элементов.
- •44. Как определить дифференциальное сопротивление по известной вах.
- •45. Можно ли получить резонансный режим в цепях с ферромагнитными элементами, изменяя только напряжение питания?
- •46. Как экспериментально определить точку резонанса токов в цепи с ферромагнитными элементами?
- •48. Покажите аналитическим путем зависимость индуктивности катушки с замкнутым сердечником от величины относительной магнитной проницаемости.
- •54. Обосновать возможность моделирования электростатического поля полем постоянных токов на проводящей бумаге?
- •55. Как определяется емкость заряженных тел по результатам измерений на модели?
- •56. Как можно построить силовые линии поля по картине поля, содержащей только эквипотенциали?
- •57. Как по картине поля определить емкость?
- •58. Дайте определение потенциала электрического поля.
- •Формула 1 — Потенциал
- •59. Дайте определение напряженности электрического поля.
- •60. Дайте определение градиента.
- •61. Что называется характеристическим сопротивлением фильтра?
- •62. Что такое коэффициент затухания, в каких единицах он измеряется?
- •63. Что такое коэффициент фазы? Как он зависит от частоты?
- •64. Почему коэффициент затухания, определяемый экспериментально, не равен нулю во всей полосе пропускания?
- •65. Что понимают под согласованной нагрузкой фильтра?
60. Дайте определение градиента.
Под градиентом скалярной функции понимают скорость изменения скалярной функции, взятой в направлении ее наибольшего возрастания. При этом в декартовой системе координат
 (23.2)
(23.2)
Для
сокращения записей различных операций
над скалярными и векторными величинами
употребляется дифференциальный оператор
Гамильтона (оператор набла)

Другими словами, запись эквивалентна записи grad, а “приписывание” слева к какой-либо скалярной функции (в нашем случае к ) оператора означает взятие градиента от этой скалярной функции.
Подставим
в уравнение Гаусса
 уравнение (23.1). Получим
уравнение (23.1). Получим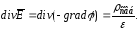 или
или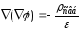
или
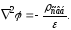 (23.3)
(23.3)
Уравнение (23.3) называется уравнением Пуассона. Частный вид уравнения Пуассона, когда свб = 0, называется уравнением Лапласа. Уравнение Лапласа запишется так 2 = 0, (23.4)
Оператор
2
= div
grad
называют оператором Лапласа или
лапласианом. В декартовой системе
координат он равен
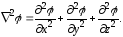 Тогда уравнение Пуассона в декартовой
системе координат запишется следующим
образом:
Тогда уравнение Пуассона в декартовой
системе координат запишется следующим
образом:
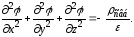 (23.5)
(23.5)
61. Что называется характеристическим сопротивлением фильтра?
Характеристическое сопротивление фильтра и его частотная зависимость определяют возможность наилучшего согласования с генератором и нагрузкой. Известная частотная зависимость характеристического сопротивления в полосе пропускания определяет возможность параллельной работы фильтров. [1]
Задано номинальное характеристическое сопротивление фильтра Ru и частота среза / с. Требуется определить параметры L и С Т - или П - образного фильтра нижних частот. [2]
62. Что такое коэффициент затухания, в каких единицах он измеряется?
Это дифференциальное уравнение, описывающее колебания заряда конденсатора. Введем обозначения:
![]() ,
, ![]() (3.46)
(3.46)
Величину β также как и в случае механических колебаний называют коэффициентом затухания, а ω0 – собственной циклической частотой колебаний.
С введенными обозначениями уравнение (3.45) примет вид
![]() (3.47)
(3.47)
Уравнение (3.47) полностью совпадает с дифференциальным уравнением гармонического осциллятора с вязким трением (формула (4.19) из раздела "Физические основы механики"). Решение этого уравнения описывает затухающие колебания вида
q(t) = q0e-btcos(wt + j) (3.48)
где
q0 –
начальный заряд конденсатора, ω = ![]() –
циклическая частота колебаний, φ –
начальная фаза колебаний. На рис. 3.17
показан вид функции q(t). Такой же вид
имеет и зависимость напряжения на
конденсаторе от времени, так как UC =
q/C.
–
циклическая частота колебаний, φ –
начальная фаза колебаний. На рис. 3.17
показан вид функции q(t). Такой же вид
имеет и зависимость напряжения на
конденсаторе от времени, так как UC =
q/C.

Рис. 3.17
Из рисунка видно, что амплитуда затухающих колебаний убывает со временем. Характеристикой затухания являетсявремя релаксации τ. Промежуток времени t = 1/b - это время, в течение которого амплитуда колебаний уменьшается в е раз. Затухание колебаний характеризуют также логарифмическим декрементом затухания λ
l = ln[A(t)/A(t+T)] = bT= T/t (3.49)
где А(t) – текущая амплитуда колебаний (А(t) = q0e-bt), Т – период колебаний. По своему смыслу величина, обратная T/t определяет число колебаний Ne, совершаемых за время релаксации. Следовательно, логарифмический декремент затухания - величина, обратная числу Ne.
Для характеристики качества колебательного контура вводят величину Q, называемую добротностью
Q = π/λ = πNe (3.50)
Таким образом, добротность показывает, насколько медленно затухают колебания в контуре.
Из (3.50), (3.49) и (3.46) можно получить выражение для добротности контура через его электрические характеристики
Q
= ![]() (3.51)
(3.51)
Описанный колебательный процесс в контуре совершается без каких-либо внешних воздействий за счет начального запаса энергии, сообщенного контуру. Такие колебания называют свободными. Электрическое сопротивление проводников приводит к затуханию свободных колебаний. Для получения незатухающих колебаний необходимо пополнять убыль энергии в контуре за счет внешних источников. Это можно осуществить, например, включив в состав контура источник переменной э.д.с. Е (рис. 3.18).