домашняя работа кпр / вопрос 1кпр

Вариант № 12

Задание №1. Как моделируется случайная величина, распределение которой отлично от равномерного распределения?

Помимо равномерного распределения случайной величины встречаются случайные величины распределения которых отлично от равномерного. К такому распределению относится распределение по закону Пуассона, показательное распределение, биноминальное распределение и нормальное распределение. Моделирование случайных величин с разным распределением – различно.

Моделирование случайной величины, распределенной по закону Пуассона.

Распределение Пуассона используют в том случае, когда число n независимых испытаний велико, а вероятность p появления события в каждом отдельном взятом испытании мала; при этих условиях вероятность появления события m раз в n испытаниях.

"Грубое" правило для применения распределения Пуассона (вместо биноминального распределения), которое состоит в том, что n должно иметь порядок не менее нескольких десятков, лучше нескольких сотен. При решении практических задач, связанных с законом Пуассона, обычно задается параметр m, а ни n, ни p неизвестны. Алгоритм моделирования случайной величины, распределенной по закону Пуассона, при заданном m следующий: выбирают n такое, чтобы вероятность p = m/n была достаточно малой (p<0.01); получают последовательность значений r₁, r₂, ..., r_n случайной величины R, равномерно распределенной на отрезке [0,1]; для каждого числа r_i, i=1, 2,...,n проверяют, выполняется ли неравенство r_i<p; если это неравенство выполняется, то полагают X_i=1, в противном случае считают X_i=0; вычисляют (это и есть значение случайной величины, распределенной по закону Пуассона).

Моделирование случайной величины с показательным распределением

Пусть случайная величина Х имеет показательное распределение с параметром . Тогда функция распределения для Имеем: .

Отсюда: . Так как R - случайная величина, равномерно распределенная на отрезке [0,1], то (1-R) также случайная величина, равномерно распределенная на отрезке [0,1]. Поэтому для моделирования случайной величины Х используют следующее соотношение: .

Моделирование случайной величины с биноминальным распределением

Напомним, что в соответствии с биномиальным распределением вероятность того, что определенное событие появиться m раз в n зависимых испытаниях:

Где p - вероятность появления события в каждом отдельно взятом испытании. Введем случайную величину Х_i - число появлений события в i-м испытании, i=1, 2, ..., n. Очевидно, что эта величина может принимать только два значения: либо 1 с вероятностью p, либо 0 с вероятностью (1-p), т.е. ряд распределения:

Xi	0	1
P	p	1-p

Тогда случайное число m появлений события в n испытаниях:

Исходя из соотношения и распределения, определение значения случайной величины m сводится к следующей процедуре:

- получают последовательность значений r₁, r₂, ..., r_n случайной величины R;

- для каждого числа r_i, i=1, 2, ..., n. Проверяют, выполняется ли неравенство r_i < p. Если неравенство выполняется, то полагают X_i=1; в противном случае считают X_i=0;

- находят сумму значений n случайных величин X_i (это и будет значение случайной величины m). Повторяя эту процедуру, получают последовательность значений m₁, m₂ ... случайной величины с биноминальным законом распределения.

Моделирование случайной величины с нормальным распределением

Для моделирования случайной величины с нормальным законом распределения можно использовать как метод обратных функций, так и методы, специально разработанные для нормального закона. При использовании ЭВМ обычно применяют метод, основанный на центральной предельной теореме: если случайные величины Х₁, Х₂, ..., Х_n независимы, одинаково распределены и их математические ожидания и дисперсии конечны, то при увеличении n закон распределения суммы (Х₁ + Х₂ + ... + Х_n) приближается к нормальному. Оказывается, что для получения хорошего приближения к нормальному распределению достаточно сравнительно небольшого числа слагаемых. Допустим, что требуется получать значения нормально распределенной случайной величины Х с математическим ожиданием МХ и дисперсией n²_x, т.е Х = N(MX, n_x).

Пусть R₁, R₂, ...,R_n - независимые случайные величины, равномерно распределенные на отрезке [0,1]. Обозначим через Y сумму этих величин:

Учитывая, что MR_i=0,5, DR_i=1/12, i=1, 2, ..., n, найдем MY=0,5n, DY=n/12.

При достаточно большом n (практически при n≥12) можно считать, что Y имеет нормальный закон распределения с математическим ожиданием MY=0,5n и дисперсией DY=n/12, т. е.

Перейдем от величины Y к стандартной нормально распределенной случайной величине:

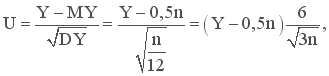
для которой MU=0, а DU=1. Перейдем от величины Х к стандартной нормально распределенной величине тогда X = MX + _xU.

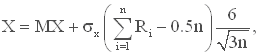
где r₁, r₂, ..., r_n - значения случайной величины R, равномерно распределенной на отрезке [0,1].