
все для алгема / Методические пособия по АГ / МП ПЗ АГ (электронный вариант) / МП ПЗ АГ ч.2 (электронный вариант)
.pdf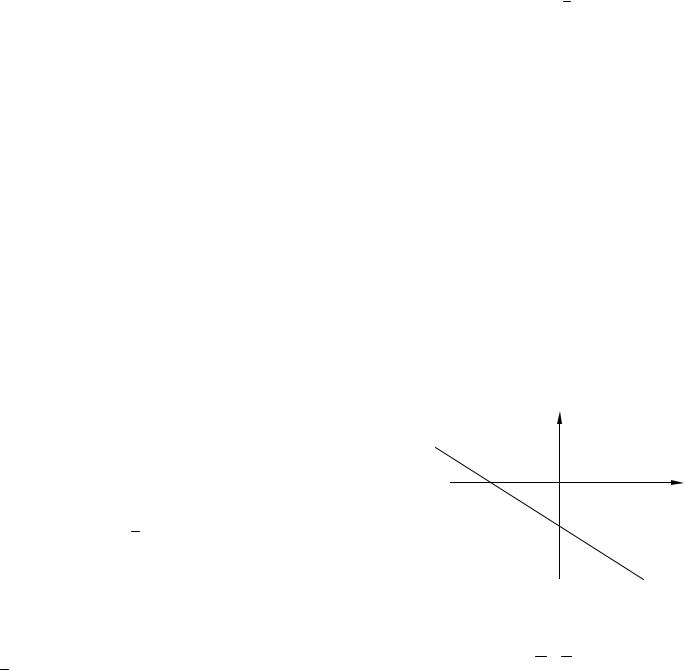
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Практическое занятие 18 Общее и каноническое уравнение прямой
Краткое содержание: понятие уравнения произвольной линии на координатной плоскости, общее уравнение прямой, неполные уравнения прямой, уравнение прямой в отрезках, уравнение прямой с угловым коэффициентом, каноническое уравнение прямой, параметрическое уравнение, взаимное расположение двух прямых на плоскости, угол между прямыми, условия параллельности и перпендикулярности двух прямых.
п.1. Теория п.1.1. Уравнение произвольной линии на координатной плоскости
Определение. Уравнение
F(x, y) 0 ,
где F(x, y) некоторая функция двух действительных аргументов, на-
зывается уравнением линии L на координатной плоскости Оху, если выполняется условие:
x, y R, |
F(x, y) 0 M(x, y) L . |
Определение. Система уравнений
x x(t) , y y(t)
где x(t), y(t) некоторые функции действительного аргумента t, назы-
вается параметрическим уравнением линии L на координатной плоскости Оху, если выполняется условие:
t T, |
x x(t) |
M(x(t), y(t)) L , |
y y(t) |
где T – некоторый промежуток числовой оси Ot, действительная переменная t называется параметром.
п.1.2. Общее уравнение прямой на плоскости Определение. Любой ненулевой вектор, перпендикулярный прямой
называется её нормальным вектором, и обозначается n (A, B) .
Теорема. (Геометрический смысл алгебраического уравнения 1-й степени с двумя неизвестными.) Алгебраическое уравнение 1-й степени
Ax By C 0 , |
(1) |
где коэффициенты А, В, С – произвольные действительные числа, одновременно не равные нулю, является уравнением прямой на коорди-
натной плоскости Оху, а вектор n (A, B) является её нормальным
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
вектором. Обратно, на координатной плоскости Оху уравнение любой прямой с нормальным вектором n (A, B) , может быть записано в виде алгебраического уравнения (1).
Определение. Уравнение прямой вида
Ax By C 0 ,
где коэффициенты А, В, С – произвольные действительные числа, одновременно не равные нулю, называется общим уравнением прямой.
Определение. Общее уравнение прямой на плоскости
Ax By C 0 ,
в котором хотя бы один из коэффициентов А, В, С равен нулю, называется неполным.
Виды неполных уравнений.
y 0 |
– уравнение оси Ох; x 0 – уравнение оси Оу; |
|
y b, |
b 0 – уравнение прямой параллельной оси Ох; |
|
x a, |
a 0 – уравнение прямой параллельной оси Оу; |
|
Ax By 0, |
A 0 B – уравнение прямой проходящей через начало |
|
координат. |
|
|
п.1.3. Уравнение прямой в отрезках и с угловым коэффициентом
у
О х
а
b
Рис.1.
Определение. Уравнение прямой вида xa by 1,
где а и b – произвольные, не равные нулю действительные числа, на- 2

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
зывается уравнением прямой в отрезках.
Теорема. (Геометрический смысл коэффициентов в уравнении пря-
мой в отрезках.) Пусть xa by 1 – уравнение прямой в отрезках. То-
гда (а; 0), (0; b) – координаты точек пересечения данной прямой с осями координат.
Определение. Углом наклона прямой к оси абсцисс называется угол поворота оси абсцисс против часовой стрелки вокруг любой её точки до положения параллельности или совпадения с данной прямой.
у
х
О
L
Рис.2
Определение. Уравнение прямой вида y kx b , где k и b – произ-
вольные действительные числа, называется уравнением прямой с угловым коэффициентом, коэффициент k называется угловым коэффициентом данной прямой.
Теорема. (Геометрический смысл коэффициентов в уравнении прямой с угловым коэффициентом.) Пусть y kx b – уравнение прямой
с угловым коэффициентом. Тогда
k tg ,
где угол равен углу наклона данной прямой к оси Ох, b – ордината точки пересечения с осью Оу.
Определение. Уравнение прямой вида
y yo k(x xo ) ,
где (xo , yo ) – координаты произвольной фиксированной точки Mo
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
данной прямой, k – её угловой коэффициент, называется уравнением прямой, проходящей через данную точку с данным угловым коэффициентом.
Определение. Уравнение прямой вида
A(x xo ) B(y yo ) 0 ,
где (xo , yo ) – координаты произвольной фиксированной точки Mo ,
лежащей на данной прямой, (A, B) n – координаты её нормального
вектора, называется уравнением прямой, проходящей через данную точку с данным нормальным вектором.
n(A,B)
L : A(x xo ) B(y yo ) 0
Mo (xo , yo )
Рис. 3
п.1.4. Каноническое и параметрическое уравнение прямой на координатной плоскости Определение. Любой ненулевой вектор, коллинеарный данной пря-
мой называется ее направляющим вектором, и обозначается s (m, n) .
Теорема. Следующая система уравнений является уравнением прямой на координатной плоскости Оху:
x xo |
mt |
, |
(2) |
|
nt |
||
y yo |
|
|
где xo , yo – координаты произвольной фиксированной точки данной
прямой, m, n – соответствующие координаты её произвольного направляющего вектора, t R – параметр.
Определение. Система уравнений (2) называется параметрическим уравнением прямой на координатной плоскости Оху.
4
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Следствие. Следующее уравнение является уравнением прямой на координатной плоскости Оху:
x xo |
|
y yo |
(3) |
|
m |
n |
|||
|
|
где xo , yo – координаты произвольной фиксированной точки данной
прямой, m, n – соответствующие координаты её произвольного направляющего вектора.
s (m,n) |
L : x xo y yo |
||
m |
n |
||
|
|||
Mo (xo , yo )
Рис. 4
Определение. Уравнение (3) называется каноническим уравнением прямой на координатной плоскости Оху.
Определение. Каноническое уравнение прямой вида
x x1 |
|
y y1 |
|||||
x |
2 |
x |
1 |
|
y |
2 |
y |
|
|
|
|
1 |
|||
называется каноническим уравнением прямой, проходящей через две различные данные точки M1 (x1;y1 ) и M2 (x2 ;y2 ) .
Теорема. (Связь нормального вектора прямой с её направляющим вектором и её угловым коэффициентом.)
1) Если n (A;B) – нормальный вектор прямой, то s (B; A) – её направляющий вектор, и, если B 0 , то k AB – её угловой коэф-
фициент.
2) Если s (m;n) – направляющий вектор прямой, то n (n; m) – её нормальный вектор, и, если m 0 , то k mn – её угловой коэффици-
ент.
3) Если k угловой коэффициент прямой, то n (k; 1) – её нормальный вектор, s (1;k) – направляющий вектор.
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
п.1.5. Взаимное расположение двух прямых на плоскости
Две прямые на плоскости могут пересекаться, совпадать или быть параллельными.
Теорема. Пусть прямые заданы общими уравнениями: L1 : A1x B1y C1 0, L2 : A2 x B2 y C2 0 . Тогда:
1) если |
|
A1 |
|
|
|
|
B1 |
|
|
|
C1 |
|
, то прямые совпадают, и система уравнений |
|||||
A2 |
B2 |
|
|
|||||||||||||||
|
|
|
|
|
|
C2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A x B y C 0 |
(4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
A2 x B2 y C2 0 |
|
|||||
имеет бесконечное множество решений; |
|
|||||||||||||||||
2) если |
|
A1 |
|
|
|
|
B1 |
|
|
|
|
C1 |
, то прямые параллельные, и система уравнений |
|||||
|
A2 |
|
|
B2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
||||
(4) не имеет решений; |
|
|
|
|
||||||||||||||
3) если |
|
A1 |
|
|
|
|
B1 |
, то прямые пересекаются и координаты точки их пе- |
||||||||||
|
A2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
ресечения являются единственным решением системы уравнений (4).
Теорема. Пусть даны канонические уравнения двух прямых: |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
L : |
|
x x1 |
|
|
y y1 |
, L |
2 |
: |
|
x x2 |
|
y y2 |
, |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
s |
1 (m1 ,n1 ), |
s |
2 (m2 ,n2 ) |
|
|
|
|
|
– |
|
их |
направляющие |
|
векторы, |
|||||||||||||||||||||||||||||||||||
M1 (x1 , y1 ), M2 (x2 , y2 ) |
– |
произвольные фиксированные точки, лежа- |
||||||||||||||||||||||||||||||||||||||||||||||||
щие на прямых L |
и L |
2 |
|
соответственно. Тогда: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) прямые совпадают, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
(s |
1 || s2 ) & (M1 L2 ) , т.е. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
m1 |
|
n1 |
и |
|
|
x1 x2 |
|
y1 y2 |
; |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
m2 |
|
|
|
n2 |
|
|
|
|
|
m2 |
|
|
|
|
|
|
n2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1 || |
|
2 ) & (M1 L2 ) , т.е. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2) прямые параллельные, если (s |
s |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m1 |
|
n1 |
|
|
|
|
и |
|
|
|
|
|
x1 x2 |
|
y1 y2 |
; |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
n2 |
m1 |
|
n1 |
|
||||||||||||||||||
3) прямые пересекаются в одной точке, если |
|
1 || |
|
2 , т.е. |
|
. |
||||||||||||||||||||||||||||||||||||||||||||
s |
s |
|||||||||||||||||||||||||||||||||||||||||||||||||
m2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Теорема. Пусть
L1 |
x x |
|
m t |
и |
L2 |
x x |
|
m |
k |
: |
1 |
1 |
: |
2 |
2 |
|
|||
|
y y1 n1t |
|
|
y y2 n2 k |
|||||
– две произвольные прямые на координатной плоскости Оху, заданные параметрическими уравнениями. Тогда:
1) если система уравнений
x |
|
m t x |
|
m |
k |
(5) |
|
1 |
1 |
2 |
2 |
|
|
y1 n1t y2 n2 k |
|
|||||
имеет единственное решение (t, k), то прямые пересекаются в одной точке, координаты которой можно найти подставляя найденные значения параметров t или k в соответствующие параметрические уравнения;
2)если система уравнений (5) не имеет решений, то прямые параллельные;
3)если система уравнений (5) имеет более одного решения, то прямые совпадают.
Теорема. Пусть n1 , n2 , s1 , s1 , k1 , k2 – соответственно нормальные век-
торы, направляющие векторы и угловые коэффициенты двух прямых, тогда один из двух углов между ними равен:
arc cos |
|
|
n1 |
|
n2 |
|
|
или arc cos |
|
|
s1 |
|
s2 |
|
|
, или arctg |
|
k2 k1 |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
| n |
1 |
| | n |
2 |
| |
|
| s | | s |
2 |
| |
|
1 |
k |
k |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
Следствие. (Условие перпендикулярности двух прямых) Пусть
n1 (A1 ; B1 ), n2 (A2 ; B2 ), s1 (m1 ; n1 ), s2 (m2 ; n2 ), k1 , k2
– соответственно нормальные векторы, направляющие векторы и угловые коэффициенты двух данных прямых. Если скалярные произведения
n1 n2 A1A2 B1B2 0 или s1 s2 m1m2 n1n2 0 ,
или произведение угловых коэффициентов k1k2 1,
то данные прямые являются перпендикулярными.
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
п.2. Список задач Список №1
1.Установить, принадлежит ли данная точка данной прямой.
2.Построить чертеж данной прямой на координатной плоскости.
3.Найти общее уравнение прямой, проходящей через данную точку, и перпендикулярной данному вектору.
4.Найти каноническое и параметрическое уравнения прямой, проходящей через данную точку, и параллельной данному вектору.
5.Найти каноническое уравнение прямой, проходящей через две данные точки.
6.Найти уравнение прямой, проходящей через данную точку с данным угловым коэффициентом.
7.Привести общее уравнение прямой к уравнению прямой в отрезках.
8.Найти общее уравнение прямой и её нормальный вектор, если известно её каноническое уравнение.
9.Найти каноническое уравнение прямой и её направляющий вектор, если известно её общее уравнение.
10.Перейти от канонического уравнения прямой к параметрическому и обратно.
11.Зная одно из уравнений прямой (общее, в отрезках, с угловым коэффициентом, каноническое, параметрическое), найти остальные виды уравнений данной прямой.
12.Найти нормальный вектор прямой, если известен её направляющий вектор, и обратно.
13.Найти нормальный вектор прямой, если известен её угловой коэффициент, и обратно.
14.Найти направляющий вектор прямой, если известен её угловой коэффициент, и обратно.
15.Выяснить взаимное расположение двух данных прямых.
16.Доказать, что две данные прямые пересекаются и найти координаты точки пересечения.
17.Найти острый угол между двумя данными прямыми.
18.Найти уравнение прямой, проходящей через заданную точку перпендикулярно (параллельно) заданной прямой.
Список №2
1.Найти проекцию данной точки на данную прямую.
2.Найти точку симметричную данной относительно данной прямой.
3.Найти уравнение прямой, на которой лежит отраженный от данной
8

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
прямой луч, если известно уравнение прямой, на которой лежит падающий луч.
4. Найти точку пересечения медиан (высот) данного треугольника.
п.3. Примеры Пример 1. Изобразить на координатной плоскости Оху прямую, за-
данную общим уравнением: 2x 3y 6 0 .
Решение. Для построения прямой достаточно знать координаты двух её точек. Координаты точек, лежащих на данной прямой, удовлетворяют её уравнению. Воспользуемся этим фактом. Положим в уравнении x 0 :
3y 6 0 .
Вычисляем у: y 2 . Следовательно, точка с координатами (0; –2)
лежит на данной прямой. Так как абсцисса этой точки равна 0, то она находится на оси ординат, т.е. точка с координатами (0; –2) является точкой пересечения данной прямой с осью ординат. Аналогично, полагая y 0 и подставляя в уравнение, находим координаты точки пе-
ресечения прямой с осью абсцисс: (3; 0). Отмечаем найденные точки на координатной плоскости Оху и проводим через них прямую. Смотрите рисунок 3.
у
О
3 х
–2
Рис.3.
Заметим, что координаты точек пересечения прямой с координатными осями можно найти, зная её уравнение в отрезках. С этой целью перенесем свободный член –6 общего уравнения прямой в правую часть:
2x 3y 6 ,
затем разделим обе части получившегося уравнения на 6: 2x6 3y6 1,
и, после сокращения, получаем уравнение прямой в отрезках: 9
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
x3 2y 1.
Отсюда видим, что прямая пересекает ось абсцисс в точке x 3 , а ось ординат – в точке y 2 .
Пример 2. Найти общее уравнение прямой, проходящей через точку А(2; –7), и перпендикулярной вектору n ( 1;4) .
Решение. 1-й способ. Воспользуемся уравнением прямой, проходящей через данную точку с данным нормальным вектором:
A(x xo ) B(y yo ) 0 ,
где (xo , yo ) – координаты произвольной фиксированной точки Mo ,
лежащей на данной прямой, (A, B) n – координаты её нормального вектора. По условию задачи искомая прямая должна проходить через точку А(2; –7), следовательно, мы можем положить xo 2, yo 7 . По условию задачи, прямая должна быть перпендикулярной вектору n ( 1;4) , следовательно, данный вектор может служить нормальным вектором для данной прямой и мы можем положить A 1, B 4 .
Подставляя эти числа в уравнение, получаем:
(x 2) 4(y 7) 0 .
Раскрывая скобки и приводя подобные члены, получаем:
x 4y 30 0 или x 4y 30 0 .
2-й способ. Воспользуемся общим уравнением прямой
Ax By C 0 ,
где (A, B) n – координаты её нормального вектора.
Так как нормальный вектор прямой дан по условию задачи: n ( 1;4) , то полагаем A 1, B 4 и подставляем эти числа в общее
уравнение прямой:
x 4y C 0 .
Искомая прямая проходит через точку А(2; –7), поэтому её координаты должны удовлетворять уравнению этой прямой. Подставляя x 2, y 7 в предыдущее уравнение, получаем:
2 4( 7) C 0 .
Отсюда находим значение коэффициента С: C 30 . Подставляя в уравнение, получаем:
10

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
x 4y 30 0 или x 4y 30 0 . Ответ: x 4y 30 0 .
Пример 3. Найти каноническое и параметрическое уравнение прямой, проходящей через точку А(2; –7) параллельно вектору s (3;5) .
Решение. Каноническое уравнение прямой имеет вид
x xo y yo , m n
где (m, n) s – координаты произвольного направляющего вектора данной прямой, (xo , yo ) – координаты произвольной фиксированной точки Mo лежащей на данной прямой.
Для написания канонического уравнения прямой у нас есть все данные. Точка А(2; –7) по условию задачи должна лежать на искомой прямой, следовательно, мы можем положить xo 2, yo 7 . По усло-
вию задачи вектор s (3;5) параллелен искомой прямой, поэтому он
является её направляющим вектором, отсюда следует, что мы можем положить m 3, n 5 . Подставляя найденные числа в каноническое
уравнение, получаем:
x 2 y 7 . 3 5
Зная каноническое уравнение прямой, легко найти её параметрическое уравнение:
x xo mt , t R ,
y yo nt
где числа xo , yo ,m,n обозначают тоже самое, что и в каноническом
уравнении прямой. Подставляя их параметрическое уравнение, получаем:
x 2 3t
y 7 5t , t R .
Заметим, что для нахождения параметрического уравнения прямой достаточно обе части канонического уравнения приравнять одной и той же букве t:
11
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
x 2 t3
y 7 t5
и разрешить уравнения получившейся системы относительно переменных х и у соответственно:
x 3t 2y 5t 7 .
Ответ: |
x 2 |
|
y 7 |
x 2 3t |
, t R . |
|
, |
|
|||||
3 |
|
5t |
||||
|
5 |
y 7 |
|
|||
Пример 4. Найти общее уравнение прямой, проходящей через точки А(3; –1) и В(–2; 5).
Решение.1-й способ. Воспользуемся уравнением прямой, проходящей через две заданные точки:
|
|
|
|
|
|
|
x x1 |
|
|
y y1 |
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
2 |
x |
1 |
|
|
y |
2 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
где (x1 , y1 ) и |
(x2 , y2 ) |
|
|
– |
|
координаты |
данных точек. Полагаем |
||||||||||||||
x1 3, y1 1, x2 |
2, y2 |
5 и подставляем эти числа в уравнение: |
|||||||||||||||||||
|
|
x 3 |
|
|
y ( 1) |
или |
|
x 3 |
|
y 1 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 3 |
5 ( 1) |
|
5 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
||||||||||||
Умножая обе части полученного уравнения на –30, получаем:
6(x 3) 5(y 1) или 6x 5y 13 0 .
2-й способ. Найдем каноническое уравнение искомой прямой:
x xo y yo . m n
По условию задачи нам известны координаты двух точек, лежащих на
прямой, поэтому вектор AB будет лежать на данной прямой и может служить её направляющим вектором. Найдем координаты вектора
AB :
AB (xB xA ; yB yA ) ( 2 3;5 ( 1)) ( 5;6) .
Т.е. в каноническом уравнении прямой мы можем положить m 5, n 6 . В качестве xo , yo мы можем взять координаты любой из
12

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
двух данных точек, т.к. обе они лежат на искомой прямой. Полагаем xo 3, yo 1 . Подставляем найденные значения m, n, xo , yo в кано-
ническое уравнение и получаем:
x 3 y 1 или 6x 5y 13 0 .5 6
Ответ: 6x 5y 13 0 .
Пример 5. Найти уравнение прямой с угловым коэффициентом k 2 , проходящей через точку М(–1; 0).
Решение. 1-й способ. Воспользуемся уравнением прямой, проходящей через данную точку с данным угловым коэффициентом:
y yo k(x xo ) ,
где (xo , yo ) – координаты произвольной фиксированной точки Mo ,
лежащей на данной прямой, k – её угловой коэффициент. Прямая проходит через точку М(–1; 0) и мы можем положить xo 1, yo 0 . Уг-
ловой коэффициент известен: k 2 . Подставляя эти данные в уравнение прямой, получаем:
y 2(x 1) .
Раскрывая скобки, находим искомое уравнение: y 2x 2 .
2-й способ. Воспользуемся уравнением прямой с угловым коэффициентом:
y kx b .
Угловой коэффициент дан по условиям задачи: k 2 . Подставляя его в уравнение, получаем:
y 2x b .
По условию задачи прямая проходит через точку М(–1; 0), следовательно, её координаты должны удовлетворять уравнению искомой прямой. Подставляя в предыдущее уравнение x 1, y 0 , получаем
уравнение с одной неизвестной b:
0 2( 1) b .
Решая последнее уравнение, находим b 2 .
Подставляем найденное значение b в уравнение с угловым коэффици-
ентом: y 2x 2 . Ответ: y 2x 2 .
13
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Пример 6. Найти нормальный вектор и общее уравнение прямой
x 6 y 2 .5 4
Решение. 1-й способ. Нормальный и направляющий векторы прямой ортогональны, и их скалярное произведение равно нулю. Из канонического уравнения прямой находим
s ( 5;4) n (4;5) .
Точка (6; –2) лежит на данной прямой, поэтому мы можем воспользоваться уравнением прямой, проходящей через данную точку, и перпендикулярную данному вектору:
A(x xo ) B(y yo ) 0 ,
или, после подстановки координат нормального вектора и точки, лежащей на прямой:
4(x 6) 5(y 2) 0 4x 5y 14 0 .
2-й способ. Умножим обе части канонического уравнения прямой на общий знаменатель. Получаем,
4x 24 5y 10 4x 5y 14 0 . Ответ: 4x 5y 14 0, n (4;5) .
Пример 7. Найти направляющий вектор и каноническое уравнение прямой 3x 2y 1 0 .
Решение. 1-й способ:
|
1) x |
|
y |
1 |
|
|
3x 2y 1 3x 2(y |
|
2 |
. |
|||
|
|
|||||
|
2 |
2 |
3 |
|
|
|
2-й способ. Выписываем координаты нормального вектора, и находим координаты направляющего вектора:
n (3; 2) s (2;3) .
Находим какое-нибудь решение уравнения 3x 2y 1 0 : x 1, y 2 ,
и записываем каноническое уравнение данной прямой:
|
|
|
|
|
|
|
x 1 |
|
y 2 |
. |
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
3 |
|
|||||
Ответ: |
|
(2;3), |
x 1 |
|
y 2 |
. |
|
|
|
||
s |
|
|
|
||||||||
2 |
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
14 |
|
|
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Пример 8. Найти параметрическое уравнение прямой |
x 1 |
|
y 2 |
. |
||||||||||
2 |
|
|
||||||||||||
|
|
x 1 |
|
y 2 |
|
|
|
|
|
3 |
|
|||
Решение. Пусть |
|
t , тогда |
t . Отсюда находим: |
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x 2t 1 |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
y 3t |
|
|
|
|
|
|
|
||
x 2t 1 |
, t |
R . |
|
|
|
|
|
|
|
|
||||
Ответ: |
2 |
|
|
|
|
|
|
|
|
|||||
y 3t |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x t 4 |
, t R . |
|||||
Пример 9. Найти каноническое уравнение прямой |
y 2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Запишем данное уравнение в виде:
x t 4y 2 0 t .
Тогда, s ( 1;0) или s (1;0) – направляющий вектор данной прямой,
точка с координатами (–4; 2) лежит на данной прямой. Осталось записать каноническое уравнение данной прямой:
x 4 y 2 .1 0
Ответ: x 1 4 y 0 2 .
Пример 10. Убедиться, что прямые x y 1 0 и x 2y 3 0 пере-
секаются и найти острый угол между ними.
Решение. Так как коэффициенты при неизвестных не пропорциональные
11 21 ,
то прямые пересекаются. Один из углов между прямыми будет равен
углу между их нормальными векторами: |
n1 |
(1, |
1), |
|
n2 |
(1, 2) : |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
1 |
. |
|||||
cos(n |
|
^ |
|
) |
n1 |
n2 |
|
|
|
|
|||||||||||||||
1 |
n2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
| n1 | | n2 | |
2 5 |
10 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Следовательно, острый угол между данными прямыми равен
15
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
|
|
1 |
|
|
1 |
|
|
arccos |
|
|
|
arccos |
|
. |
|
10 |
10 |
||||||
|
|
|
|
|
Ответ: arccos 110 .
Пример 11. Выяснить взаимное расположение двух прямых
L1 : 3x 4y 11 0 |
и L2 : 2x 3y 8 0 , и если они пересекаются, |
найти точку их пересечения.
Решение. Так как коэффициенты при неизвестных не пропорциональны:
32 43 ,
то прямые пересекаются. Для вычисления координат точки их пересечения решим систему
3x 4y 11 2x 3y 8
с помощью формул Крамера. Определитель системы
|
|
3 |
4 |
|
9 8 1 0 , |
|
|
||||
|
|
2 |
3 |
|
|
следовательно, система имеет единственное решение, т.е. данные прямые пересекаются. Вычисляем координаты точки пересечения:
x |
|
11 |
4 |
|
1, y |
|
|
3 |
11 |
|
2 , |
|
|
|
|
|
|||||||||
|
|
8 |
3 |
|
|
|
|
2 |
8 |
|
|
|
|
|
x |
x |
1, y |
y |
|
2 . |
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
Ответ: прямые пересекаются в точке (–1; 2).
Пример 12. Найти точку пересечения прямых:
x 2t 1 L1 : 3x 4y 11 0 и L2 : y 3t 2 .
Решение. Решаем систему уравнений
x 2t 1
y 3t 2 .
3x 4y 11 0
16

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Подставляем неизвестные х и у из первых уравнений системы в последнее уравнение, и находим:
3(2t 1) 4(3t 2) 11 0 или t 1.
Подставляя найденное значение параметра t в первые два уравнения системы, находим: x 3, y 5 .
Ответ: (3; 5).
п.4. Задачи Задачи для аудиторного решения 18
1. Построить прямую, заданную уравнением 2x y 4 0 , и записать уравнение этой прямой в отрезках.
2.Найти общее уравнение прямой, проходящей через точку А(4; 3) перпендикулярно вектору n (1; 2) .
3.Найти уравнение прямой с угловым коэффициентом, если её угло-
вой коэффициент равен k 23 и известно, что прямая проходит че-
рез точку С(0; –1).
4.Найти каноническое и параметрическое уравнение прямой, проходящей через точку А(–1; 2) параллельно вектору s (3; 4) .
5.Найти общее уравнение прямой, проходящей через точки А(–3; 4) и
В(1; –2).
6. |
Найти |
|
точку |
пересечения двух прямых |
3x 4y 29 0 и |
|||||||||||||
|
2x 5y 19 0 и угол между ними. |
|
||||||||||||||||
7. |
Выяснить взаимное расположение прямых: |
|
||||||||||||||||
|
а) x 3 y 1 0, 3x y 3 1 0 ; |
|
|
|
||||||||||||||
|
б) x 3 y 1 0, x y 3 1 0 ; |
|
|
|
||||||||||||||
|
в) y |
|
|
2 |
x 1, y |
x |
|
1; г) |
y |
|
2 |
x 1, y x |
2 1; |
|||||
|
|
2 |
|
|
2 |
|||||||||||||
|
|
|
x 1 |
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x 7 |
3t |
|
|
|
|
|
||||
|
д) |
|
|
|
y 1, y 1 t , t R ; |
|
|
|
||||||||||
|
3 |
|
|
|
|
|
||||||||||||
|
|
|
x 1 |
|
|
y |
6 |
|
x 1 3t |
|
|
|
|
|
||||
|
е) |
|
|
|
|
|
|
|
, |
y 1 4t , t |
R . |
|
|
|
||||
|
|
4 |
|
|
3 |
|
|
|
|
|||||||||
8. |
Найти все виды уравнений прямой 4x 3y 12 0 , ее угловой ко- |
|||||||||||||||||
эффициент, нормальный и направляющий векторы, точки пересечения с координатными осями, и постройте её чертеж на коорди-
17
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
натной плоскости.
9.Дана прямая 2x 3y 4 0 . Составить уравнение прямой, прохо-
дящей через точку М(–2; 0): а) параллельно данной прямой; б) перпендикулярно данной прямой.
Задачи повышенного уровня сложности 18
10.Составить уравнение прямой, если точка N(4; 5) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
11.Дан треугольник АВС: А(–2; 1), В(3; 5), С(10; 3). Найдите: а) общее уравнение прямой на которой лежит сторона АС; б) направляющий вектор высоты BD и её параметрическое уравнение; в) координаты точки D.
12.Найти проекцию точки А(1; –3) на прямую 2x y 5 0 .
13. Найти координаты точки N, симметричной точке |
М(–3;4) отно- |
сительно прямой 4x y 1 0 . |
|
14. Даны уравнения сторон треугольника АВ: 3x 2y 6 0 , АС: 7x y 31 0 , ВС: 2x 7y 38 0 . Найти уравнение перпен-
дикуляра, опущенного из вершины В на медиану, проведенную из вершины А.
15.Даны две противоположные вершины квадрата А(–1; 3) и С(6; 2). Найти уравнения его сторон.
16.Из точки А(–5; 6) выходит луч света под углом arctg ( 2) к
оси Ох и отражается от оси Ох, а затем отражается от оси Оу. Найти уравнения прямых, по которым направлены все три луча.
17.Найти уравнение отраженного от прямой 2x 3y 8 0 луча, лежащего на прямой x 2y 3 0 .
18.Найти уравнение прямой, проходящей через точку с координатами
(2; 1) под углом 45o к прямой 2x 3y 4 0 .
19. Составить уравнения сторон треугольника, зная координаты одной из его вершин (4; –1) и уравнения двух биссектрис: x 1 и
yx 1.
20.Составить уравнение прямой, проходящей через начало координат, зная, что длина её отрезка, заключённого между прямыми
2x y 5 0 |
и 2x y 10 0 , равна 10 . |
18

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
Домашнее задание 18. Общее и каноническое уравнение прямой
1.Напишите все виды уравнений для прямой, проходящей через точки А(2; 1) и В(4; 1), ее угловой коэффициент, нормальный и направляющий векторы, точки пересечения с координатными осями.
2. Найти точку пересечения двух прямых 3x 4y 29 0 и 2x 5y 19 0 и угол между ними.
3.Найти уравнение прямой образующей с осью Оу угол 30o и пересекающей ее в точке (0; – 6).
4.Дан треугольник с вершинами А(3; 2), В(3; 8), С(6; 2). написать уравнения сторон треугольника.
5*. |
Определить |
при |
каком |
значении |
р |
прямая |
(p2 p)x (3 p)y 3p 1 0 : а) параллельна оси Ох; б) парал-
лельна оси Оу; в) проходит через начало координат; г) перпендикулярна прямой y x .
6*. Луч света, пройдя через точку А(2; 3) под углом к оси Ох, отразился от нее и прошел через точку В(–5; 4). Найти угол и координаты точки отражения луча.
Самостоятельная работа 18
Вариант 1.
1.Определение направляющего вектора прямой.
2.Составьте параметрические уравнения прямой, проходящей через точки А(–2; 6) и В(4; 2) и выпишите ее направляющий вектор.
3.Составьте общее уравнение прямой, проходящей через точку А(1; –
2)перпендикулярно биссектрисе первого и третьего координатных
углов и выпишите ее нормальный вектор. Вариант 2.
1.Определение нормального вектора прямой.
2.Составьте каноническое уравнение прямой, проходящей через точки А(1; 4) и В(–4; 1), и выпишите ее направляющий вектор.
3.Составьте общее уравнение прямой, проходящей через точку А(1; –
1) перпендикулярно биссектрисе второго и четвертого координатных углов и выпишите ее нормальный вектор.
Вариант 3.
1.Определение общего уравнения прямой.
2.Найдите параметрическое уравнение прямой, проходящей через вершину А треугольника АВС параллельно стороне ВC, если А(2; –
19
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 18, с.22
3), В(3; 0), С(0; –2).
3.Составьте общее уравнение прямой, проходящей через точку А(1; –
4)перпендикулярно прямой x 4y 1 и выпишите ее нормальный
вектор. Вариант 4.
1.Определение канонического уравнения прямой на плоскости.
2.Найдите уравнение прямой в отрезках, проходящей через вершину
Втреугольника АВС параллельно стороне АC, если А(2; –3), В(3; 0), С(0; –2).
3.Составьте общее уравнение прямой, проходящей через точку А(1; –
1)перпендикулярно прямой x 2y 1 и выпишите ее нормальный
вектор.
п.5. Вопросы и задачи для самоконтроля 18 Обозначения
1.Обозначение направляющего вектора прямой на плоскости.
2.Обозначение нормального вектора прямой на плоскости.
3.Обозначение свободного коэффициента общего уравнения прямой на плоскости.
4.Обозначение абсциссы точки пересечения прямой с осью Ох.
5.Обозначение ординаты точки пересечения прямой с осью Оу.
6.Обозначение углового коэффициента прямой на координатной плоскости.
7.Обозначение угла между прямыми.
Определения
1.Определение уравнения линии на плоскости.
2.Определение параметрического уравнения линии на плоскости.
3.Определение направляющего вектора прямой.
4.Определение нормального вектора прямой на плоскости.
5.Определение угла наклона прямой к оси абсцисс.
6.Определение канонического уравнения прямой.
7.Определение уравнения прямой, проходящей через две точки.
8.Определение параметрического уравнения прямой на плоскости.
9.Определение общего уравнения прямой на плоскости.
10.Определение уравнения прямой, проходящей через заданную точ-
20
