все для алгема / АГ-2 Преподавателям / АГ-2 СР / Мойвариант
.doc|
1 Вариант 1. Определение квадратной матрицы. 2. Определение перестановки конечного множества. 3. Докажите, что если обратная матрица для матрицы А существует, то она единственная. 4. Найти inv (1,2,5,4,6,3)
5.
Пусть
а)
6.
Вычислить определитель
7.
Найти матрицу обратную данной методом
Гаусса: 8. Решить матричное уравнение:
9.
Решить систему
10.
Решить и исследовать систему, в
зависимости от значения параметра
|
2 Вариант 1. Определение диагональной матрицы. 2. Определение обратной матрицы. 3. Классификация систем линейных уравнений по множеству решений. 4. Найти inv (1,3,5,4,6,2)
5.
6.
Вычислить определитель
7.
Найти матрицу обратную данной методом
Гаусса: 8. Решить матричное уравнение:
9.
Решить систему
10.
Решить и исследовать систему, в
зависимости от значения параметра
|
|
1 Вариант 1. Определение квадратной матрицы. 2. Определение перестановки конечного множества. 3. Докажите, что если обратная матрица для матрицы А существует, то она единственная. 4. Найти inv (1,2,5,4,6,3)
5.
Вычислить определитель
6.
Найти матрицу обратную данной методом
Гаусса: 7. Решить матричное уравнение:
8.
Решить систему
|
2 Вариант 1. Определение диагональной матрицы. 2. Определение обратной матрицы. 3. Классификация систем линейных уравнений по множеству решений. 4. Найти inv (1,3,5,4,6,2)
5.
Вычислить определитель
6.
Найти матрицу обратную данной методом
Гаусса: 7. Решить матричное уравнение:
8.
Решить систему
|
|
1 Вариант 1. Определение квадратной матрицы. 2. Определение перестановки конечного множества. 3. Докажите, что если обратная матрица для матрицы А существует, то она единственная. 4. Найти inv (1,2,5,4,6,3)
5.
Вычислить определитель
6.
Найти матрицу обратную данной методом
Гаусса: 7. Решить матричное уравнение:
8.
Решить систему
|
2 Вариант 1. Определение диагональной матрицы. 2. Определение обратной матрицы. 3. Классификация систем линейных уравнений по множеству решений. 4. Найти inv (1,3,5,4,6,2)
5.
Вычислить определитель
6.
Найти матрицу обратную данной методом
Гаусса: 7. Решить матричное уравнение:
8.
Решить систему
|
|
1. Определение ранга матрицы.
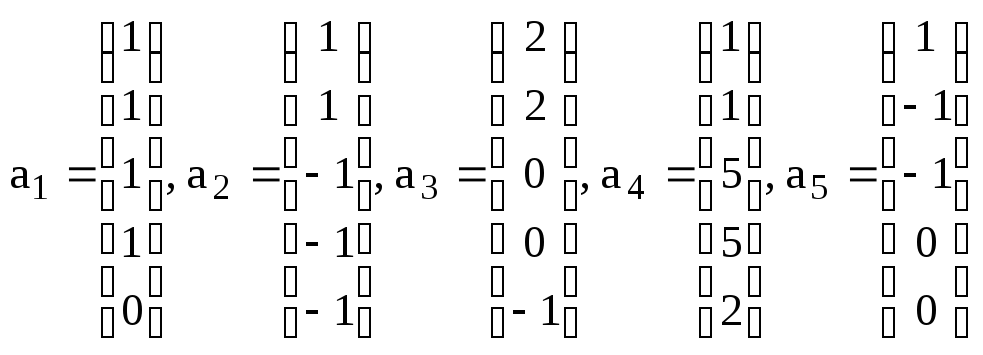
2. Дана система
столбцов:
а) Доказать, что данная система линейно зависимая; б) выразить один из векторов системы через предыдущие вектора этой системы; в) Найти базис и размерность линейной оболочки, натянутой на данную систему столбцов.
3. Докажите, что
следующая система столбцов является
базисом пространства столбцов
4. Определение суммы подпространств.
5. Дана система
столбцов:
Пусть
а) базис и размерность L; б) базис и размерность М;
в) базис и
размерность
г) размерность
д)
базис
|
1. Определение ранга матрицы.
2. Дана система
столбцов:
а) Доказать, что данная система линейно зависимая; б) выразить один из векторов системы через предыдущие вектора этой системы; в) Найти базис и размерность линейной оболочки, натянутой на данную систему столбцов.
3. Докажите, что
следующая система столбцов является
базисом пространства столбцов
4. Определение суммы подпространств.
5. Дана система
столбцов:
Пусть
а) базис и размерность L; б) базис и размерность М;
в) базис и
размерность
г) размерность
д)
базис
|
|
1. Определение ранга матрицы.
2. Дана система
столбцов:
а) Доказать, что данная система линейно зависимая; б) выразить один из векторов системы через предыдущие вектора этой системы; в) Найти базис и размерность линейной оболочки, натянутой на данную систему столбцов.
3. Докажите, что
следующая система столбцов является
базисом пространства столбцов
4. Определение суммы подпространств.
5. Дана система
столбцов:
Пусть
а) базис и размерность L; б) базис и размерность М;
в) базис и
размерность
г) размерность
д) базис
|
1. Определение ранга матрицы.
2. Дана система
столбцов:
а) Доказать, что данная система линейно зависимая; б) выразить один из векторов системы через предыдущие вектора этой системы; в) Найти базис и размерность линейной оболочки, натянутой на данную систему столбцов.
3. Докажите, что
следующая система столбцов является
базисом пространства столбцов
4. Определение суммы подпространств.
5. Дана система
столбцов:
Пусть
а) базис и размерность L; б) базис и размерность М;
в) базис и
размерность
г) размерность
д) базис
|
|
1. Дано отображение f векторных пространств: а) докажите, что f - линейное отображение соответствующих векторных пространств; б) найдите матрицу линейного отображения f относительно указанных базисов данных векторных пространств; в) найдите ядро и образ линейного отображения f.
1.1. Пусть
В качестве базисов взять канонические базисы.
1.2. Пусть
2. Найти: 1) собственные значения; 2) собственные векторы; собственные подпространства; 3) базис из собственных векторов (если он существует); 4) определить диагонализируема ли данная матрица.
а)
3. Решить систему:
|
1. Дано отображение f векторных пространств: а) докажите, что f - линейное отображение соответствующих векторных пространств; б) найдите матрицу линейного отображения f относительно указанных базисов данных векторных пространств; в) найдите ядро и образ линейного отображения f.
1.1. Пусть
В качестве базисов взять канонические базисы.
1.2. Пусть
2. Найти: 1) собственные значения; 2) собственные векторы; собственные подпространства; 3) базис из собственных векторов (если он существует); 4) определить диагонализируема ли данная матрица.
а)
3. Решить систему:
|
|
1. Дано отображение f векторных пространств: а) докажите, что f - линейное отображение соответствующих векторных пространств; б) найдите матрицу линейного отображения f относительно указанных базисов данных векторных пространств; в) найдите ядро и образ линейного отображения f.
1.1. Пусть
В качестве базисов взять канонические базисы.
1.2. Пусть
2. Найти: 1) собственные значения; 2) собственные векторы; собственные подпространства; 3) базис из собственных векторов (если он существует); 4) определить диагонализируема ли данная матрица.
а)
3. Решить систему:
|
|
1. Дано отображение f векторных пространств:
а) докажите, что f - линейное отображение соответствующих векторных пространств;
б) найдите матрицу линейного отображения f относительно указанных базисов данных векторных пространств;
в) найдите ядро и образ линейного отображения f.
1.1. Пусть
![]() - отображение из пространства столбцов
высоты 2 в пространство столбцов высоты
3, которое задается правилом:
- отображение из пространства столбцов
высоты 2 в пространство столбцов высоты
3, которое задается правилом:
 .
.
В качестве базисов взять канонические базисы.
1.2. Пусть
![]() - пространство векторов на плоскости
как направленных отрезков, отложенных
от начала координат и задана прямоугольная
декартовая система координат с
ортонормированным базисом
- пространство векторов на плоскости
как направленных отрезков, отложенных
от начала координат и задана прямоугольная
декартовая система координат с
ортонормированным базисом
![]() .
Поставим в соответствие каждому вектору
пространства
.
Поставим в соответствие каждому вектору
пространства
![]() вектор, полученный из данного поворотом
вокруг его начала на
вектор, полученный из данного поворотом
вокруг его начала на
![]() против часовой стрелки.
против часовой стрелки.
2. Задача. Найти:
1) собственные значения;
2)собственные векторы матриц, рассматриваемых как операторы умножения в пространстве столбцов над полем С;
3) собственные подпространства;
4) базис из собственных векторов (если он существует);
5) определить диагонализируема ли данная матрица.
а)
![]() ;
б)
;
б)
 ;
;
3. Решить систему:
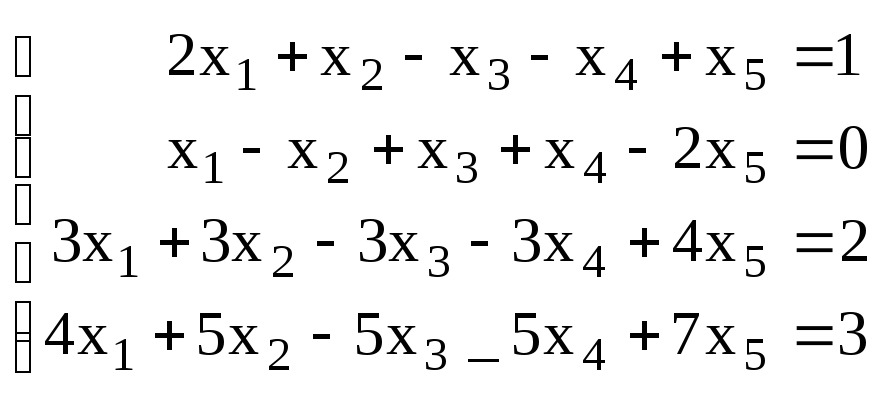

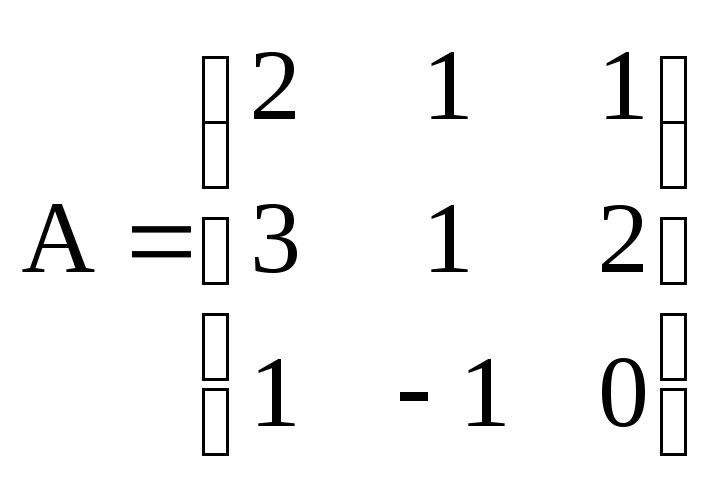 .
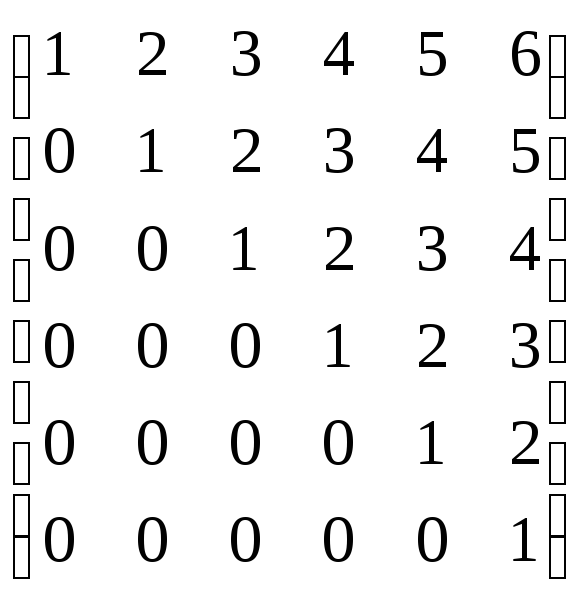
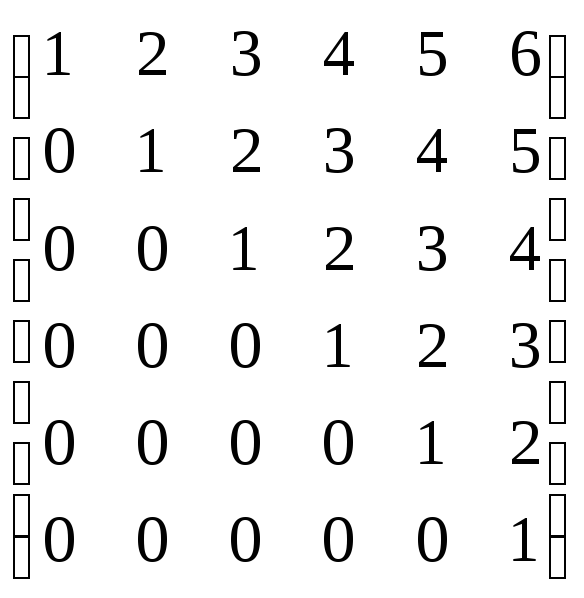
Вычислить:
.
Вычислить: .
.
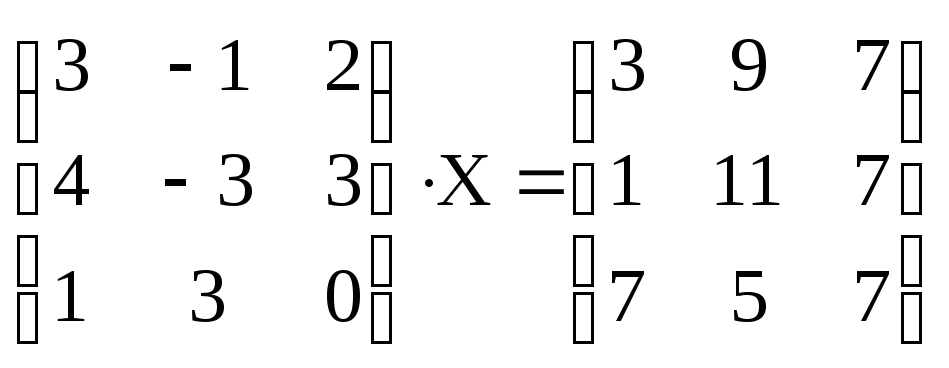 .
.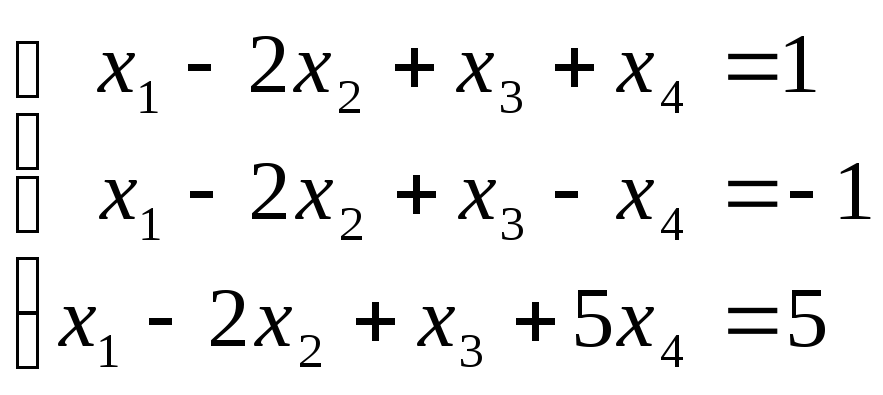
 .
. .
.
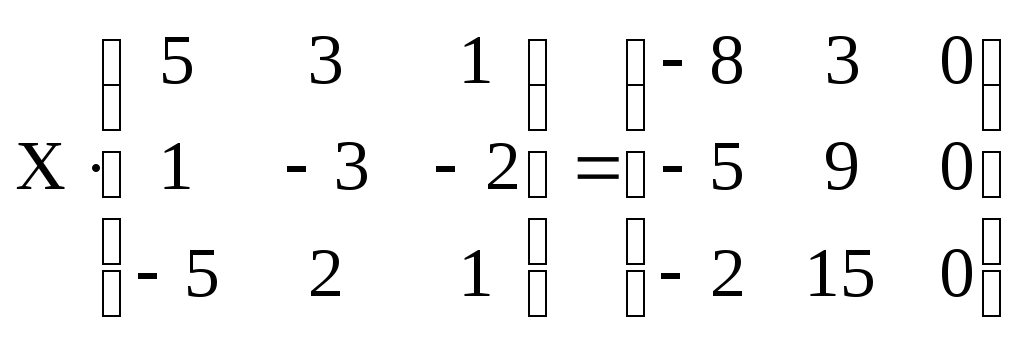 .
.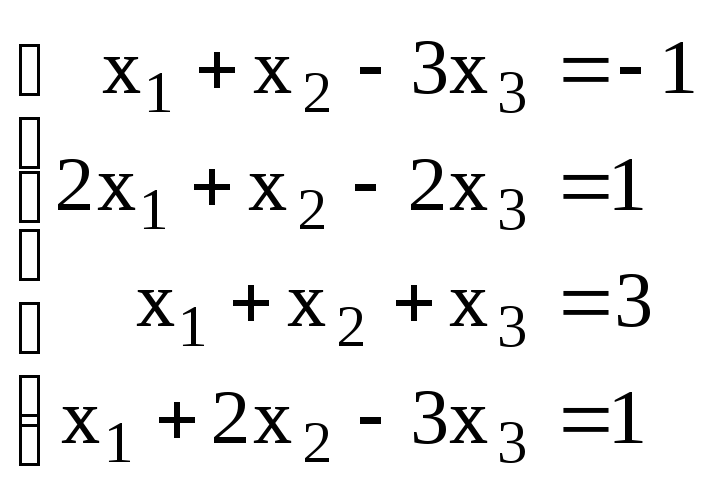
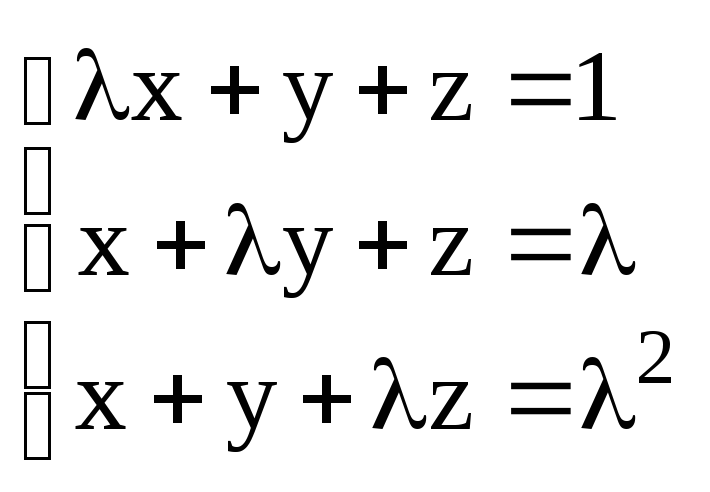 .
. .
.
 .
.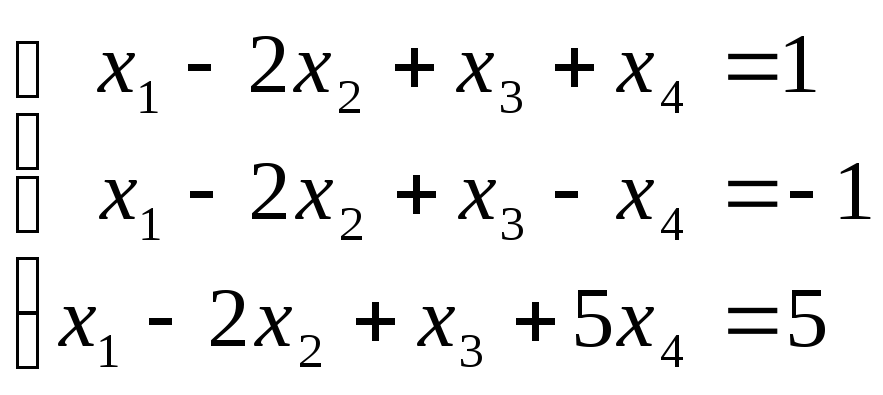
 .
.
 .
.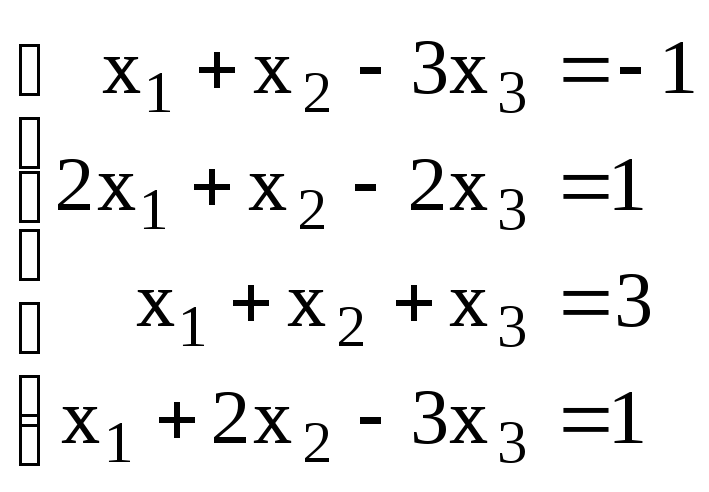
 .
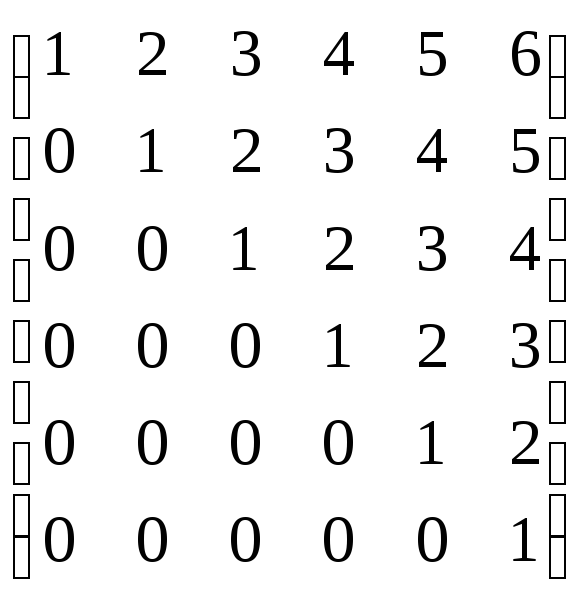
.
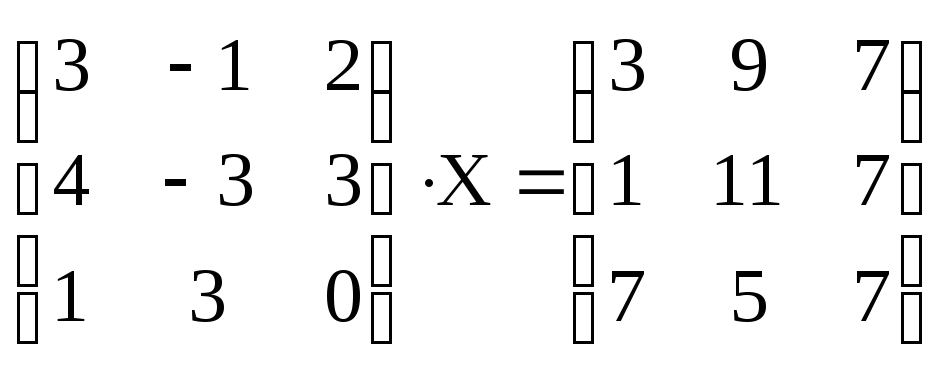 .
.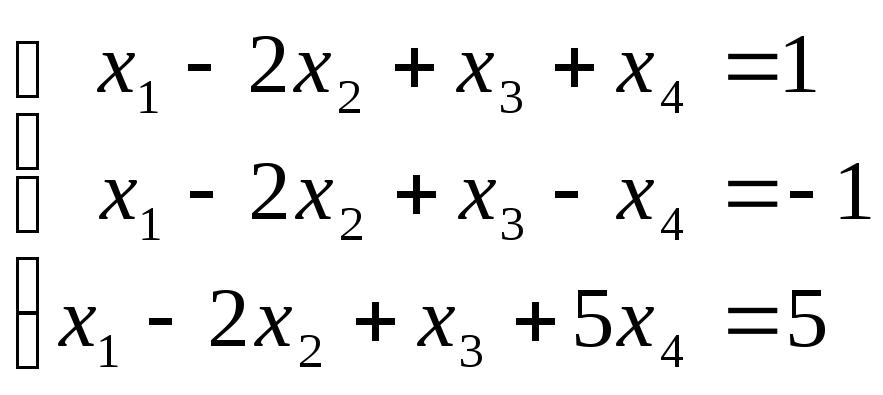
 .
.
 .
.
 .
. и найдите
координаты вектора
и найдите
координаты вектора
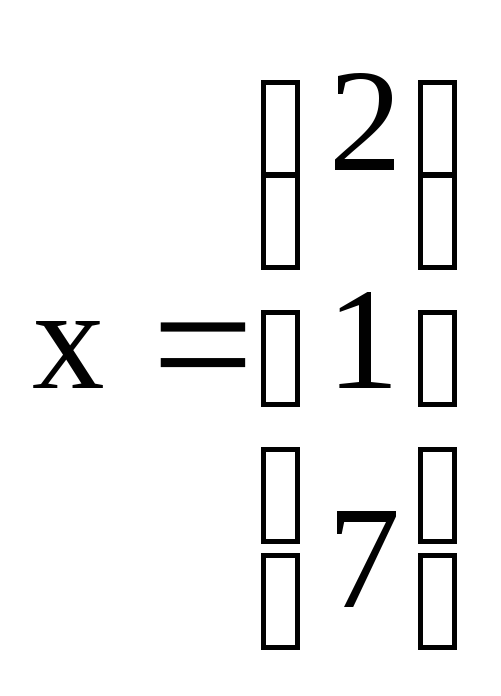 относительно этого базиса.
относительно этого базиса.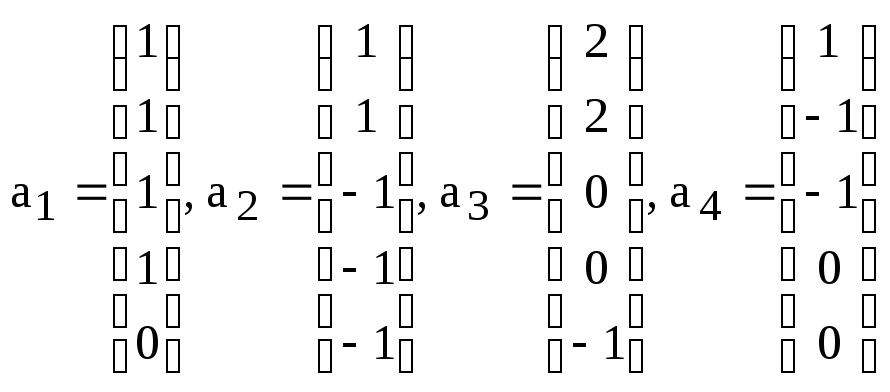 .
. .
.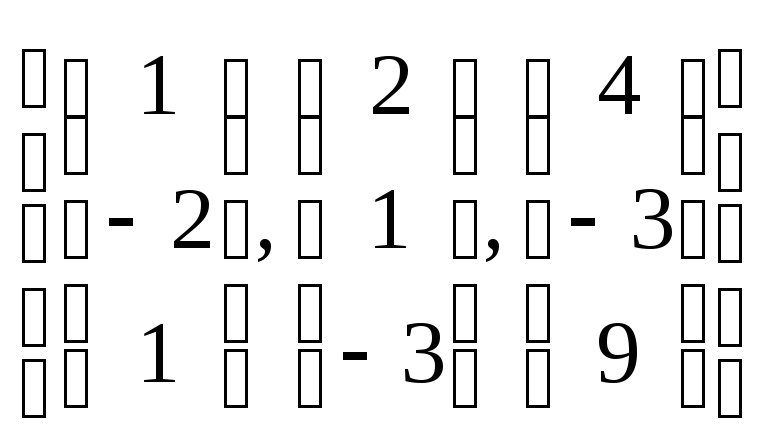 и найдите
координаты вектора
и найдите
координаты вектора
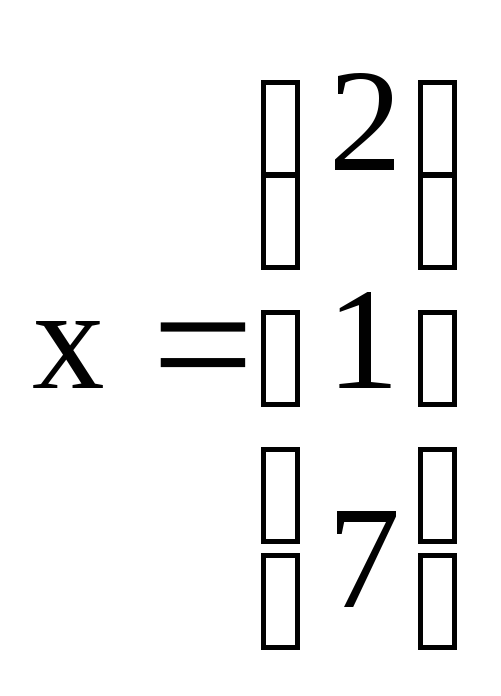 относительно этого базиса.
относительно этого базиса.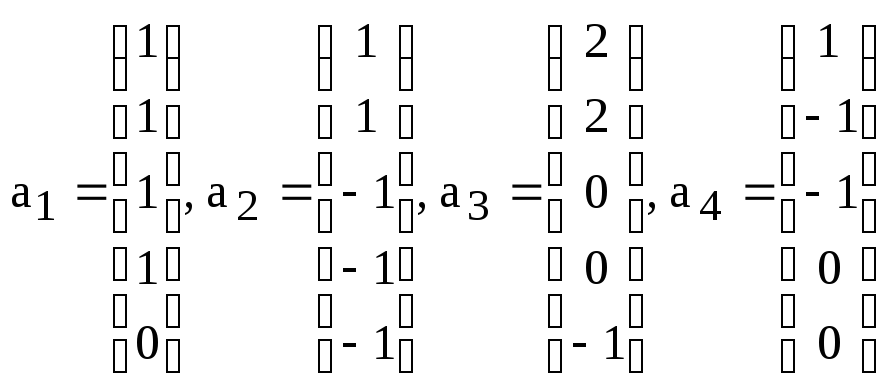 .
.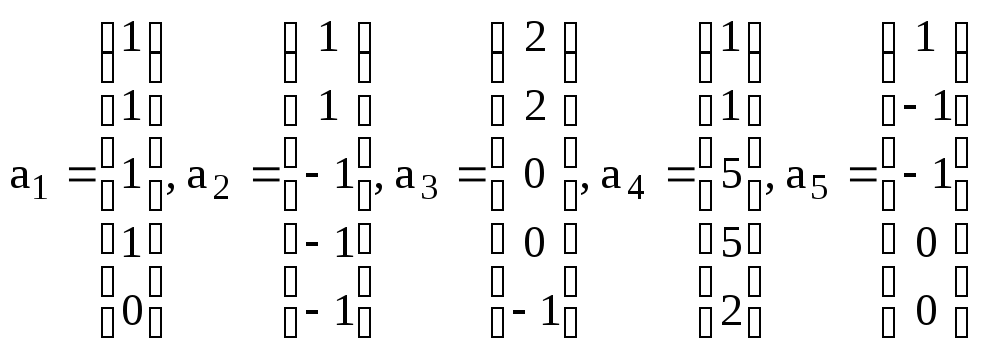 .
.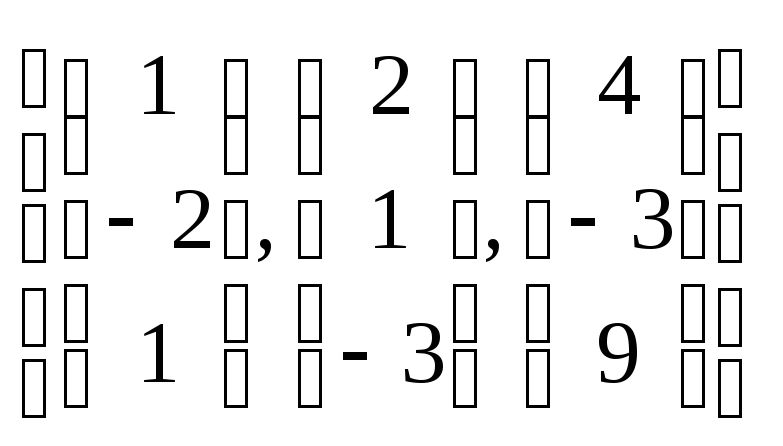 и найдите
координаты вектора
и найдите
координаты вектора
 относительно этого базиса.
относительно этого базиса.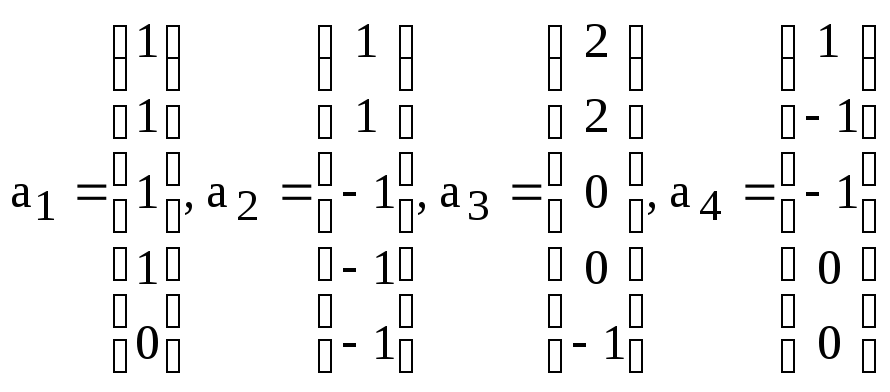 .
.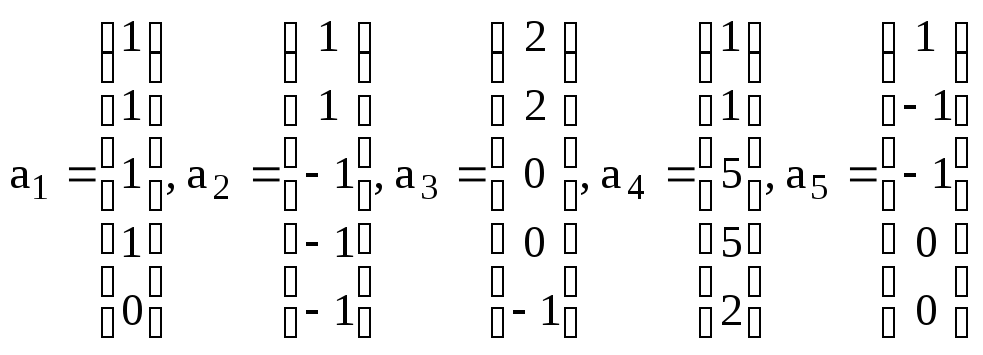 .
.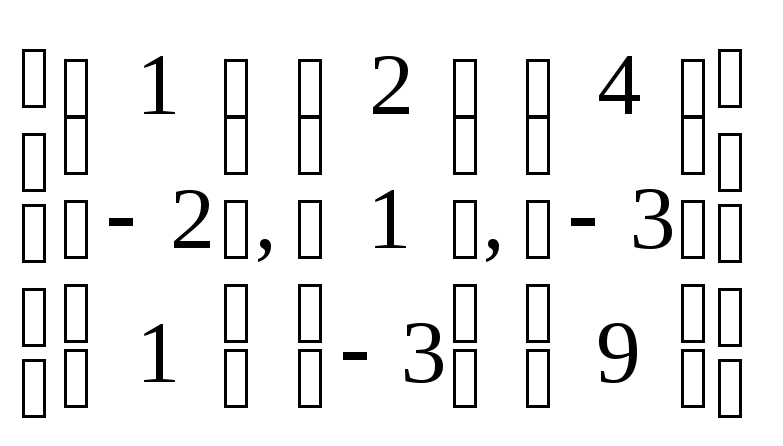 и найдите
координаты вектора
и найдите
координаты вектора
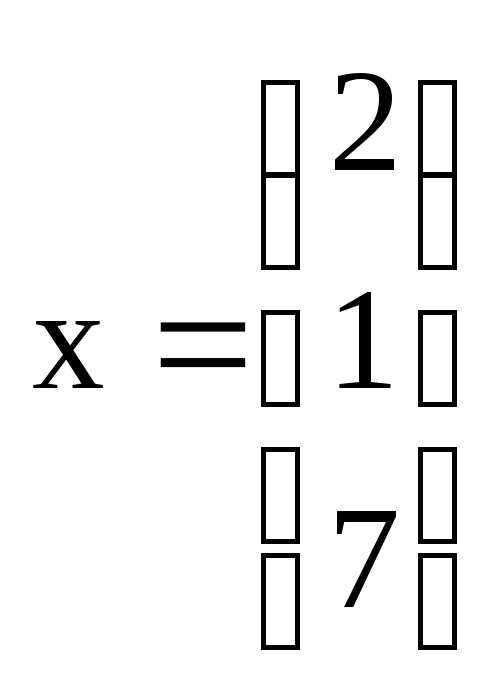 относительно этого базиса.
относительно этого базиса.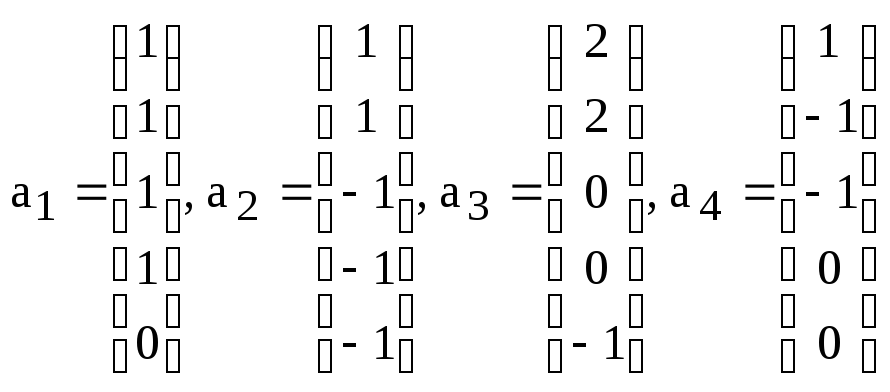 .
.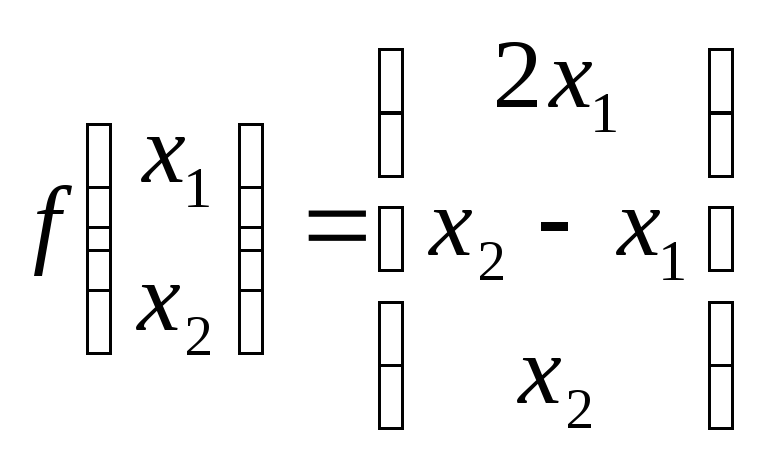 .
. ;
;
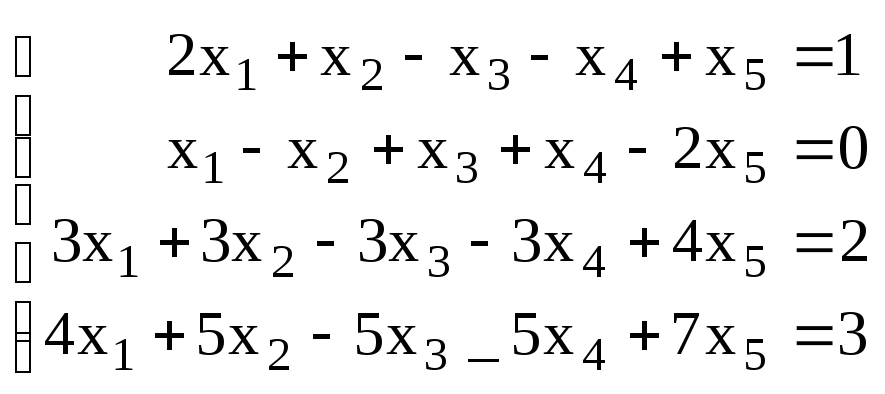
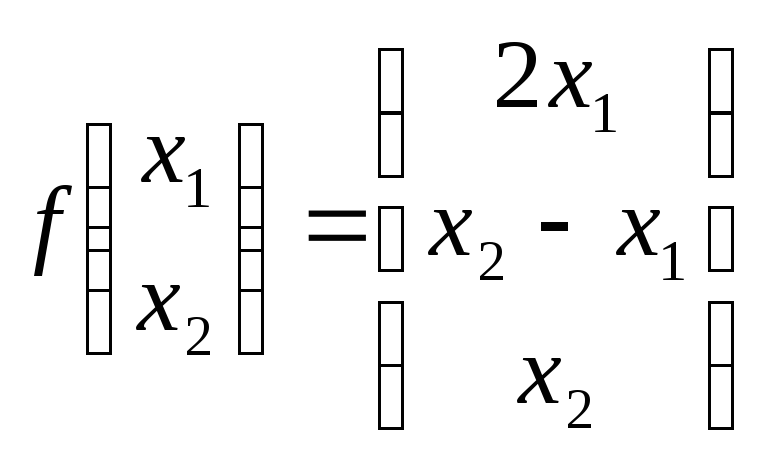 .
. ;
;
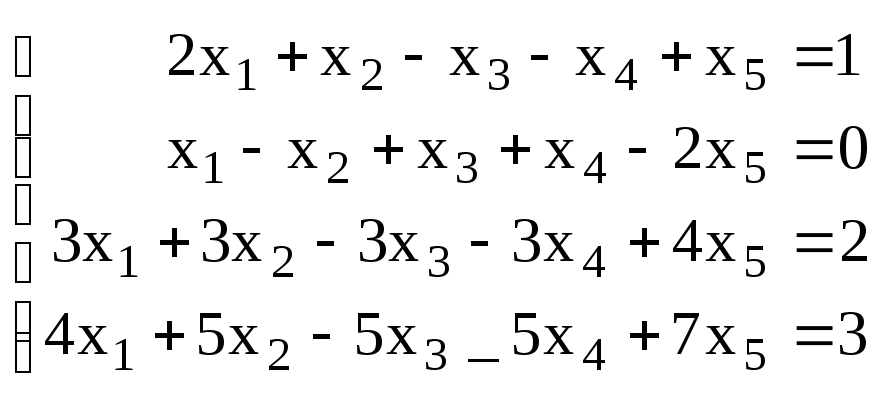
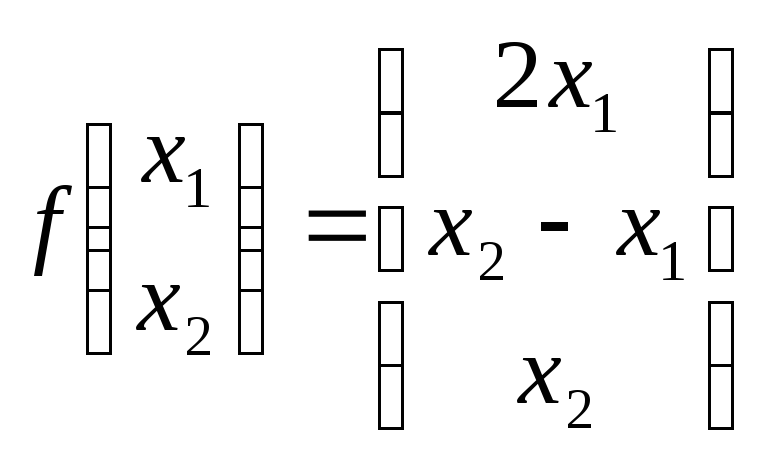 .
. ;
;