25.Задача.

Возьмем цепь (см. рисунок ниже). Известно, что

.

Нужно найти ток:

Частота тока и напряжения одна и та же, значит необходимо найти и.

Решение:

Выполним решение двумя способами:

1. непосредственным интегрированием с использованием заданных функций;

2. символическим методом;

1 Способ:

Т.к. вектора тока и напряжения вращаются с одинаковой частотой, их взаимное расположение будет зафиксировано. Тогда пусть , и будем считать, что

.

Записываем второй закон Кирхгофа для цепи:

.

Здесь мы возьмем определенный интеграл, чтобы не выпускать начальные значения и смотреть, что происходит в цепи. Далее определенным интегралом пользоваться не будем (впоследствии будет показано, почему). Подставляем в это уравнение начальные:

.

Мы уже говорили, что реакцией цепи на синусоидальное воздействие будет синусоидальное воздействие той же частоты. Поэтому в установившемся режиме (а мы сейчас рассматриваем установившиеся режимы) сумма . В общем случае эти слагаемые обусловлены переходным процессом. Казалось бы, вполне естественно писать определенный интеграл. Но- некая «предыстория», это напряжение, которое имеется в нулевой момент времени на конденсаторе (это напряжение появляется в результате переходного процесса, по сути- интеграл отдо).

Итак, к этому материалу мы вернемся в следующем семестре, а пока будем писать неопределенный интеграл. Теперь решим получившееся уравнение, взяв два удобных момента времени:

1. :

;

2. :

;

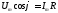Получили два уравнения с двумя неизвестными. Решаем:

.

Сдвиг фаз находим делением :

.

Из этого уравнения следует, что угол сдвига фаз между током и напряжением определяется только параметрами самой цепи.

Вернемся к первоначальному уравнению для этой задачи и посмотрим размерность:

,

получаем, что и-реактивные сопротивления– сопротивления индуктивности и емкости на переменном токе, измеряются, как и активные сопротивления, в Омах. График зависимости реактивных сопротивлений отизображен на рисунке.

2 Способ:

Теперь те же самые выражения получим символическим методом:

.

Видно, что все вектора вращаются с одной частотой, у всех величин будет фактор 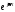. Тогда, сокращая наи выносяв левой части за скобку, получим:

,

где - комплексное сопротивление цепи.

Важно!!!

Здесь именнонеперечеркнуто!!!будет иметь другой смысл:

При этом комплексное сопротивление индуктивности и емкости соответственно имеют вид:

,

.

Комплексные величины равны тогда и только тогда, когда равны их амплитуды и фазы:

,

.

Посмотрим на реактивные сопротивления, на и. Пусть для тока есть

,

тогда для индуктивности:

Из последнего уравнения следует, что ибудут располагаться так, как показано на рисунке (действительно,). Аналогично для емкости:

.

Тогда вектор напряжения относительно вектора тока будет направлен вниз (см. рисунок).

Итак, если вращение вектора тока и вектора напряжения по кратчайшему пути происходят против часовой стрелки, то такой угол сдвига фаз является положительным, если по часовой стрелке – отрицательным.

26.