Matematika / Методические указания для самостоятельной работы студентов I курса

Министерство образования и науки Российской Федерации

Казанский государственный архитектурно-строительный университет

Кафедра высшей математики

Элементы векторной и линейной алгебры.

Аналитическая геометрия.

Методические указания для самостоятельной работы студентов I курса

Казань

2012

c Казанский государственный архитектурно-строительный университет, 2012c www.5354.ru

5354.ru

Содержание

5354.ru

2

Основные понятия и формулы векторной алгебры

1. Если a11, a12, a21, a22 – числа, то определителем второго порядка называется число, определяемое формулой

a21 a22

2.Определитель третьего порядка определяется равенством

a31 a32 a33

3.Разложение вектора по базисным векторам

a = axi + ayj + azk или a = (ax; ay; az).

Если a = AB, где точки A и B заданы координатами A(x1; y1; z1) и B(x2; y2; z2), то

ax = x2 x1; ay = y2 y1; az = z2 z1:

4. Длина (модуль) вектора

q

jaj = a2x + a2y + a2z;

расстояние между точками A и B

p

jABj = (x2 x1)2 + (y2 y1)2 + (z2 z1)2:

5.Скалярное произведение векторов, заданных своими проекциями. Если векторы заданы своими проекциями:

3

7. Векторное произведение векторов, заданных своими проекциями

i j k

[a; b] = ax ay az :

bx by bz

8.Смешанное произведение векторов. Если векторы заданы своими проекциями:

a = (ax; ay; az); b = (bx; by; bz); c = (cx; cy; cz);

то смешанное произведение векторов

ax ay az

(a; b; c) = bx by bz :

cx cy cz

Элементы аналитической геометрии (в пространстве)

Здесь и далее даётся решение примеров и задач. Соответствующий теоретический материал, а именно, основные понятия и вывод соответствующих формул, можно найти в книгах [1] - [3].

Рассмотрим следующую задачу. Даны координаты вершин пирамиды:

A1(x1; y1; z1); A2(x2; y2; z2); A3(x3; y3; z3); A4(x4; y4; z4):

Возьмём для определённости A1(7; 6; 3), A2(6; 5; 8), A3(3; 6; 8), A4(8; 4; 1). Требуется:

1.Найти длину ребра A1A2.

Согласно формуле A1A2 = (x2 x1; y2 y1; z2 z1) имеем

A1A2 = (6 7; 5 6; 8 3) или A1A2 = ( 1; 1; 5). Пусть ax = 1, ay = 1, az = 5. Тогда искомая длина

2.Найти угол между ребрами A1A2 и A1A4.

Имеем A1A2 = ( 1; 1; 5). Аналогичным образом находим A1A4 = (1; 2; 2). Обозначим bx = 1, by = 2, bz = 2.

Косинус искомого угла ищем по формуле

cos ' = (A1A2; A1A4)

jA1A2jjA1A4j 5354.ru

4

3.Найти угол между ребром A1A4 и гранью A1A2A3.

Найдем: вектор A1A3 = (x3 x1; y3 y1; z3 z1) или A1A3 = ( 4; 0; 5) и

нормальный вектор плоскости A1A2A3, т. е. вектор N

N = [A1A2; A1A3] = 1 1 5 = 5i 15j 4k:

4 0 5

Так как нормальный вектор плоскости N = ( 5; 15; 4) и направляющий вектор прямой a = A1A4 = (1; 2; 2) известны, то синус искомого угла

4.Найти площадь грани A1A2A3. Искомую площадь S ищем по формуле

1

S = 2j[A1A2; A1A3]j:

Тогда с учётом найденного в пункте 3 векторного произведения, имеем:

S= 12p( 5)2 + ( 15)2 + ( 4)2 = 12 p266:

5.Найти объём пирамиды A1A2A3A4.

Для нахождения искомого объёма V воспользуемся формулой

5

6.Найти уравнение прямой A1A2.

Воспользуемся уравнением прямой, проходящей через две точки:

7.Найти уравнение плоскости A1A2A3. Воспользуемся уравнением плоскости в виде:

A(x x0) + B(y y0) + C(z z0) = 0:

Здесь нормальный вектор плоскости N = (A; B; C) найден в пункте 3 и имеет вид N = ( 5; 15; 4), а в качестве точки (x0; y0; z0) лежащей на плоскости, берем точку A1(7; 6; 3). Тогда уравнение плоскости A1; A2; A3 имеет вид:

5(x 7) 15(y 6) 4(z 3) = 0

или

5x + 15y + 4z 137 = 0:

8.Найти уравнение высоты, опущенной из вершины A4 на грань A1A2A3. Воспользуемся уравнением прямой в виде

Здесь в качестве направляющего вектора a прямой берем вектор

a = N = ( 5; 15; 4), а в качестве начальной точки x0; y0; z0) берем точку A4(8; 4; 1). Тогда искомое уравнение высоты имеет вид

Элементы аналитической геометрии (на плоскости).

Кривые второго порядка

Здесь требуется привести к каноническому виду уравнения кривых второго порядка и сделать чертеж.

1.2x2 + 2y2 = 8.

Разделим обе части уравнения на “два” и получим:

x2 + y2 = 4:

5354.ru

6

Это уравнение окружности с центром в начале координат – точке O(0; 0) и радиусом R = 2 (Рис. 1).

2.8x2 + 2y2 = 8.

Разделим обе части уравнения на “восемь” и получим

x2 + y2 = 1:

1 4

Это каноническое уравнение эллипса с центром в начале координат – точке O(0; 0); осями симметрии, совпадающими с осями координат; полуоси эллипса a = 1, b = 2 (Рис. 2).

Y

2

1

X

-1

-2

7

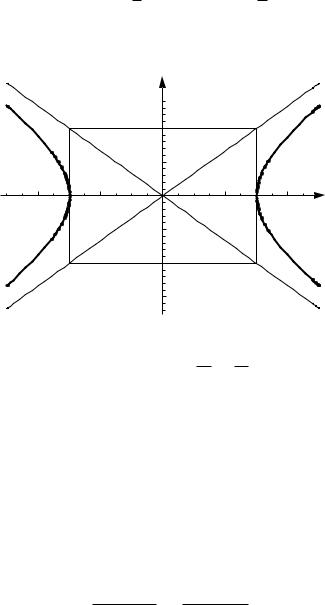
Это каноническое уравнение гиперболы с центром в начале координат; осями симметрии, совпадающими с осями координат; с действительной полуосью a = 3 и мнимой полуосью b = 2 (Рис. 3). Прямоугольник со сторонами 2a = 6 и 2b = 4 есть основной прямоугольник гиперболы. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гиперболы. Их уравнения имеют вид

4.y2 + 2y 4x2 + 8x 7 = 0.

Дополним в уравнении члены, содержащие x и y, до полных квадратов. Получим (y2 + 2y + 1) 1 4(x2 2x + 1) + 4 7 = 0 или

(y + 1)2 4(x 1)2 = 4:

Разделим обе части уравнения на “четыре” и получим

(y + 1)2 (x 1)2 = 1: 4 1

Это каноническое уравнение гиперболы с центром в точке O(1; 1); осями симметрии, параллельными осям координат; с действительной полуосью b = 2 и мнимой полуосью a = 1 (Рис. 4).

5354.ru

8

5.2y2 4y + x = 1 Дополняя в уравнении члены, содержащие y, до полного квадрата, получим

2(y2 2y + 1) 2 + x = 1 или 2(y 1)2 = 3 x,

откуда

(y 1)2 = 12(x 3):

Получили уравнение параболы с вершиной в точке O1(3; 1) и осью симметрии, параллельной оси Ox; при этом параметр параболы p = 14 (Рис. 5).

Рис. 5: Парабола (y 1)2 = 12(x 3)

5354.ru

9

Элементы линейной алгебры.

Решение системы линейных уравнений

Рассмотрим следующую задачу. Дана система трёх линейных уравнений для трёх неизвестных:

8

> x1 + 2x2 + x3 = 8

<

3x1 + 2x2 + x3 = 10

>

: 4x1 + 3x2 2x3 = 4:

Требуется решить систему

по формулам Крамера;

с помощью матриц;

методом Гаусса.

1.Решение системы по формулам Крамера. Вычислим предварительно опре-

делитель системы:

и определители, получаемые из , заменой соответствующего столбца на столбец свободных членов

Тогда, по формулам Крамера, найдем

2. Решение системы с помощью матриц. Выпишем матрицу системы

5354.ru

10