Тервер лабораторные / ИДЗ / шаблон лабы
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ
Индивидуальное домашнее задание
по дисциплине
«Теория вероятностей»
на тему:
«Выборочный коэффициент ранговой корреляции Спирмена и проверка гипотезы о его значимости»
|
|
Студент |
|
|
|
Литвинов Е.В. |
|
||||||||
|
|
|
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
|
|
Группа |
|
АИ-10 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
Принял |
|
|
|
|
|
||||||||
|
|
|
|
|
|
Корнеев А.М. |
|
||||||||
|
|
ученая степень, звание |
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
Липецк 2012
1. Теория
Допустим, что объекты генеральной совокупности обладают двумя качественными признаками. Под качественным подразумевается признак, который невозможно измерить точно, но он позволяет сравнивать объекты между собой и, следовательно, расположить их в порядке убывания или возрастания качества. Для определенности будем всегда располагать объекты в порядке ухудшения качества. При таком «ранжировании» на первом месте находится объект наилучшего качества по сравнению с остальными; на втором месте окажется объект «хуже» первого, но «лучше» других, и т. д.
Пусть выборка
объема
содержит независимые объекты, которые
обладают двумя качественными признаками
А
и В.
Для оценки степени связи признаков
вводят, в частности, коэффициент ранговой
корреляции Спирмена.
Для практических целей использование ранговой корреляции весьма полезно. Например, если установлена высокая ранговая корреляция между двумя качественным признаками изделий, то достаточно контролировать изделия только по одному из признаков, что удешевляет и ускоряет контроль.
Расположим сначала
объекты выборки в порядке ухудшения
качества по признаку А при допущении,
что все объекты имеют различное качество
по обоим признакам (случай, когда это
допущение не выполняемся, рассмотрим
ниже). Припишем объекту, стоящему на i-м
месте, число – ранг
,
равный порядковому номеру объекта.
Например, ранг объекта, занимающего
первое место,
;
объект, расположенный на втором месте,
имеет ранг
,
и т. д. В итоге получим последовательность
рангов по признаку А:
.
Расположим теперь
объекты в порядке убывания качества по
признаку В и припишем каждому из них
ранг
,
однако (для удобства сравнения рангов)
индекс i
при y
будет по-прежнему равен порядковому
номеру объекта по признаку А. Например,
запись
означает,
что по признаку А объект стоит на втором
месте, а по признаку В — на пятом.
В итоге получим две последовательности рангов:
по признаку А
по признаку В
Заметим, что в
первой строке индекс i
совпадает с порядковым номером объекта,
а во второй, вообще говоря, не совпадает.
Итак, в общем случае
.
Рассмотрим два «крайних случая».
1. Пусть ранги по
признакам А и В совпадают при всех
значениях индекса
.
В этом случае ухудшение качества по
одному признаку влечет ухудшение
качества по другому. Очевидно, признаки
связаны: имеет место «полная прямая
зависимость».
2. Пусть ранги по
признакам А и B
противоположны в том смысле, что если
,
то
;
если
,
то
;
…; если
,
то
. В этом случае ухудшение качества по
одному признаку влечет улучшение по
другому. Очевидно, признаки связаны —
имеет мест «противоположная зависимость».
На практике чаще будет встречаться промежуточный случай, когда ухудшение качества по одному признаку влечет для некоторых объектов ухудшение, а для других - улучшение качества. Задача состоит в том, чтобы
оценить связь
между признаками. Для ее решения
рассмотрим ранги
как возможные значения случайной
величины X, а
как возможные значения случайной
величины У. Таким образом, о связи между
качественными признаками А и В можно
судить по связи между случайными
величинами X и У, для оценки которой
используем коэффициент корреляции.
Вычислим выборочный коэффициент корреляции случайных величин X и У в условных вариантах:
приняв в качестве
условных вариант отклонения
,
.
Каждому рангу
соответствует только один ранг
,
поэтому частота любой пары рангов с
одинаковыми индексами, а следовательно,
и любой пары условиях вариант с одинаковыми
индексами равна единице:
=
1. Очевидно, что частота любой пары
вариант с разными индексами равна
нулю. Учитывая, кроме того, что среднее
значение отклонения равно нулю, т.е.
,
получим более простую формулу вычисления
выборочного коэффициента корреляции:
. (*)
Таким образом,
надо найти
,
и
.
Выразим
через известные числа — объем выборки
n
и разности рангов
.
Заметим, что поскольку средние значения
рангов
и
равны между собой, то
.
Используем последнее равенство:
.
Следовательно,
Учитывая, что (см. далее пояснение)
, (**)
имеем
Отсюда
. (***)
Остается найти
и
.
По определению выборочной дисперсии,
учитывая, что
,
и используя (**), получим
.
Отсюда среднеквадратическое отклонение
.
Аналогично найдем
Следовательно,
.
Подставив правые части этого равенства и соотношения (***) в (*), окончательно получим выборочный коэффициент ранговой корреляции Спирмена
, (****)
где
.
Пояснение. Покажем,
что
.
Действительно, учитывая, что
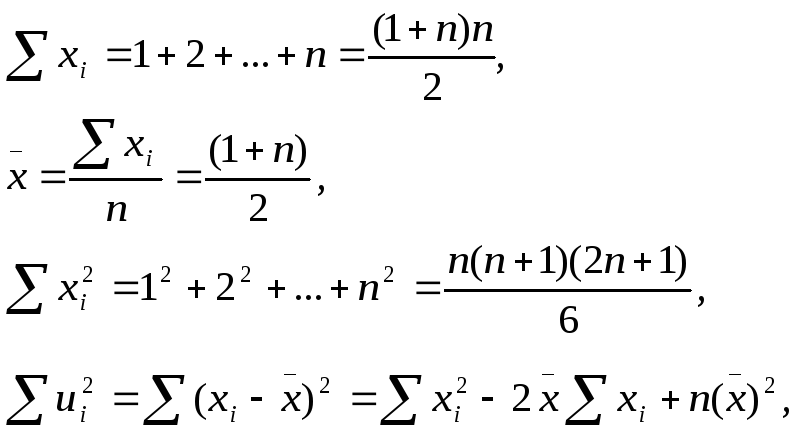
после элементарных выкладок получим
.
Аналогично можно показать, что
.
Приведем свойства выборочного коэффициента корреляции Спирмена.
Свойство 1. Если между качественными признаками А и В имеется «полная прямая зависимость» в том смысле, что ранги объектов совпадают при всех значениях i, то выборочный коэффициент ранговой корреляции Спирмена равен единице.
Действительно,
подставив
в (****),
получим
С в о й с т в о 2.
Если между
качественными признаками А и В имеется
«противоположная зависимость» в том
смысле, что рангу
соответствует ранг
;
рангу
соответствует ранг
;
…; рангу
соответствует ранг
,
то выборочный коэффициент ранговой
корреляции Спирмена равен минус единице.
Действительно,
.
Следовательно,
Подставив
в (****),
окончательно получим
Свойство 3. Если между качественными признаками А и В нет ни «полной прямой», ни «противоположной» зависимостей, то коэффициент заключен между -1 и +1, причем чем ближе к нулю его абсолютная величина, тем зависимость меньше.
Приведем правило,
позволяющее установить значимость или
незначимость ранговой корреляции связи
для выборок объема
.
Если
,
то пользуются таблицами.
Правило.
Для того чтобы при уровне значимости
проверить нулевую гипотезу о равенстве
нулю генерального коэффициента ранговой
корреляции
Спирмена при конкурирующей гипотезе
,
надо вычислить критическую точку:
,
где n—объем
выборки,
—
выборочный коэффициент ранговой
корреляции Спирмена,
- критическая точка двусторонней
критической области, которую находят
по таблице критических точек распределения
Стьюдента, по уровню значимости
и числу степеней свободы k
= n—2.
Если
—нет
оснований отвергнуть нулевую гипотезу.
Ранговая корреляционная связь между
качественными признаками незначима.
Если
— нулевую гипотезу отвергают. Между
качественными признаками существует
значимая ранговая корреляционная связь.
2. Примеры
Пример 1
Найти выборочный коэффициент ранговой корреляции Спирмена по данным ранга объектов выборки.
1) Пусть дана выборка
|
133 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
141 |
142 |
143 |
144 |
145 |
Расположим в порядке ухудшения по признаку А:
|
x |
134 |
136 |
145 |
141 |
133 |
143 |
135 |
137 |
138 |
139 |
140 |
142 |
144 |
Припишем объекту, стоящему на i-ом месте, число - ранг, равный порядковому номеру объекта:
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
Расположим в порядке ухудшения по признаку B:
|
y |
136 |
134 |
144 |
140 |
142 |
145 |
141 |
138 |
139 |
143 |
133 |
135 |
137 |
Ранги признака В:
|
yi |
2 |
1 |
13 |
11 |
12 |
3 |
4 |
9 |
10 |
6 |
5 |
7 |
8 |
тогда
|
di |
-1 |
1 |
-10 |
-7 |
-7 |
3 |
3 |
-1 |
-1 |
4 |
6 |
5 |
5 |
|
di^2 |
1 |
1 |
100 |
49 |
49 |
9 |
9 |
1 |
1 |
16 |
36 |
25 |
25 |
|
∑di^2= |
322,00 |
|
n= |
13,00 |
|
r= |
0,12 |
2)
|
Выборка |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
y |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
|
yi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
di |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
di^2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑di^2= |
0,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n= |
14,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r= |
1,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3)
|
Выборка |
115 |
117 |
118 |
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
115 |
117 |
118 |
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 |
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
y |
126 |
125 |
124 |
123 |
122 |
121 |
120 |
119 |
118 |
117 |
115 |
|
yi |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
di |
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
|
di^2 |
100 |
64 |
36 |
16 |
4 |
0 |
4 |
16 |
36 |
64 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑di^2= |
440,00 |
|
|
|
|
|
|
|
|
|
|
|
n= |
11,00 |
|
|
|
|
|
|
|
|
|
|
|
r= |
-1,00 |
|
|
|
|
|
|
|
|
|
|