
Konspekt_Melnika.unlocked
.pdf
ДИАГРАММЫ ИНТЕНСИВНОСТИ ПЕРЕХОДОВ
Они содержат вершины состояний, соединенные дугами переходов. Дугам присваиваются числа, соответствующие интенсивностям переходов, а не вероятностям. При этом дуги переходов состояний отсутствуют. Интенсивность перехода – это интенсивность, с которой может увеличиваться или уменьшаться число заявок в системе. Увеличиваться может с интенсивностью λ, а уменьшаться может с интенсивностью μ.
K-1 |
|
K |
K+1 |
|
|
||
|
|
|
|
|
μ |
|
μ |
|
|
|
Будем понимать под величиной потока вероятности произведение вероятности состояния на интенсивность ухода из этого состояния. Алгебраические уравнения, описывающие работу системы можно записать исходя из законов равенства потоков состояний для вероятностей: суммарный выходной поток всегда равен суммарному входному.
Pk −1λ + Pk +1μ = Pk (λ + μ)
СИСТЕМА M/M/N С БЛОКИРОВКОЙ
При построении системы алгебраических уравнений кроме правила равенства потоков для состояний можно использовать правило равенства потоков вероятностей через сечение диаграммы.
μ1 = w
P0 = p P0λ = P1μ P1λ = P2μ
P2λ = P3μ
P1 = λμ P0 = wp P2 = λμ P1 = w2 p
P3 = λμ P2 = w3 p Pi = wi p
n+2
åPi =1
i=0
p = 1− w+
1− wn 3

СИСТЕМА С ОТКАЗАМИ
λ |
μ |
n+1
åPi =1
i=0
p = |
|
|
1− w |
- т.е. отнять одно состояние. |
|
1 |
− wn+2 |
||||
|
|
||||
МНОГОКАНАЛЬНОЕ СМО С ОТКАЗАМИ M/M/n/0
μ
K1
μ
n |
K2 |
λ
μ
K3
μ – интенсивность обслуживания в канале. Если не хватает каналов, то заявка уходит.
λ |
λ |
|
λ |
λ |
0 |
1 |
2 |
. . . |
n |
|
μ |
2μ |
3μ |
nμ |
n – максимальное количество заявок.
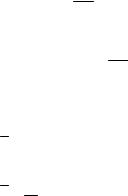
P0λ = P1μ
P1λ = 2P2 μ
P2λ = 3P3μ
P1 = wp
P = |
1 |
wP = |
w2 |
p |
|||||||
|
|
|
|
||||||||
2 |
2 |
|
1 |
|
|
2! |
|
||||
|
|
|
|
|
|
|
|
||||
P = |
1 |
wP = |
w3 |
p |
|||||||
|
|
|
|
||||||||
3 |
3 |
|
2 |
|
|
3! |
|
||||
|
|
|
|
|
|
|
|
||||
P = |
wi |
|
p |
|
(1) |
|
|
||||
|
|
|
|
|
|
|
|||||
i |
|
i! |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
w |
i |
|
|
|
|
|
p = [å |
|
p] |
(2) |
||||||||
i! |
|||||||||||
|
|
i=0 |
|
|
|
|
|
||||
Выражения (1) и (2) называются формулами Эрланга. Вероятность того, что заявка, придя в систему получит отказ:
Pотк = Pn = wn p n!
Относительная пропускная способность – это вероятность того, что заявка обслужится:
Q =1- Pотк =1- wn p n!
A = λQ - интенсивность выходного потока, т.е. обслуженных заявок. Среднее число занятых каналов:
k = 0× P0 +1× P0 +...+ n× P0
Необходимо узнать, сколько должно работать каналов, чтобы обеспечить интенсивность А:
k = μA
ФОРМУЛА ЛИТТЛА
Эта формула связывает между собой среднее время пребывания заявок в системе (Wc) и среднюю длину очереди (Lc) в этой системе.
Рассмотрим систему массового обслуживания произвольной структуры. Важно: в этой системе очередь не ограничена и предполагается наличие при работе системы наличие стационарного режима (λ/μ>1).
Если система работает длительное время, то λ=μ.
X(t) – количество заявок пришедших в систему к моменту времени t. Y(t) – количество заявок ушедших из системы к моменту времени t.
Нарисуем график:
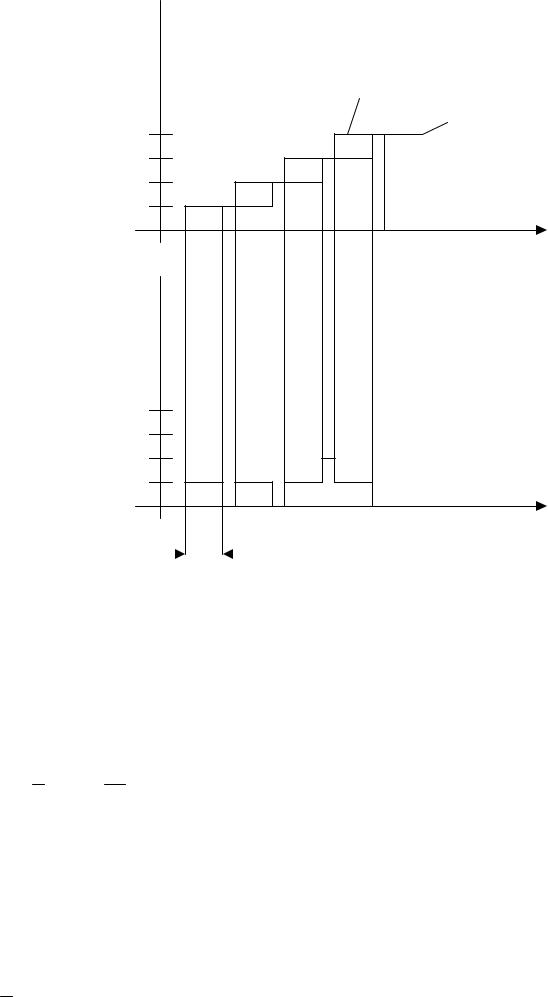
X(t) 
Y(t)
X(t)
Y(t)
4
3
2
1
t1 |
t2 |
t3 |
t4 |
t5 |
Z(t) 
4
3
2
1
|
|
|
|
|
t1 |
|
|
t2 |
t4 |
t5 |
|
|
|
|
|
|
|
|
|
|
|
t3 |
|
|
|
|
|
|
|
|
ti – время пребывания заявки в системе |
||||
|
Z (t) = Y (t) − X (t) - количество заявок, находящихся в момент времени t в системе. |
||||||||||
|
|
|
Нас интересует среднее значение числа заявок, находящихся в системе на протяжении работы в этой |
||||||||
системе. |
|
|
|
|
|
||||||
1 |
T |
Z (t)dt = L |
|
|
|
|
|
||||
|
T |
ò |
|
|
|
|
|
||||
|
c |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
Интеграл – площадь фигуры под графиком функции J. В нашем случае для каждой заявки – это прямоугольник. Длина – время пребывания заявки в системе, высота – единица.
Lc = T1 åti ×1 = λλT åti
λT - количество заявок пришедших в систему.
Lc = λWc
Lоч = λWоч - 2ая формула Литтла.
ОДНОКАНАЛЬНАЯ СМО С НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ М/M/1/∞
λ <1
μ- т.е. все заявки, пришедшие в очередь, будут обслужены. Вероятности состояний будут конечны.

|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
. . . |
|
|
|
i |
|
|
|
i+1 |
. . . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
|
|
|
|
|
|
m |
|
|||||||
P0λ = P1μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P1λ = P2μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P1 = wp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P = w2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = wi p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
åPi |
=1 |
=> åwi p =1=> påwi =1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y=0 |
|
|
|
|
|
|
|
|
|
i=0 |
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Последняя сумма – сумма геометрической прогрессии. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
s = |
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
- q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p =1− w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вероятности будут убывать. Т.е. у нас самая большая вероятность – вероятность простоя. |
|
|||||||||||||||||||||||||||
Среднее число заявок в системе |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Lc = å∞ |
|
iPi =å∞ |
i(1-ϖ ) = (1-ϖ )å∞ |
iϖ i = ω(1-ϖ )å∞ |
iϖ i−1 |
=ϖ (1-ϖ )å∞ |
d |
(ϖ i ) = |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
i=0 |
|
|
|
i=0 |
|
|
i=0 |
|
|
i=0 |
|
|
|
|
|
|
i=0 dϖ |
|
||||||
=ϖ (1-ϖ ) |
d |
å∞ |
(ϖ i ) =ϖ (1-ϖ ) |
d |
|
ϖ |
=ϖ (1-ϖ ) |
1 |
|
|
= |
ϖ |
|
|
||||||||||||||
dϖ |
dϖ 1-ϖ |
(1-ϖ ) |
2 |
1-ϖ |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|||||||||||||
W = |
Lc |
|
= |
|
ϖ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
c |
|
|
|
λ |
|
|
|
λ(1-ϖ ) |
- среднее время пребывания заявок в системе. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Среднее число заявок в очереди Это среднее число заявок, находящихся в системе минус среднее число заявок находящихся под обслуживанием.
Lоч = Lc - Lобс
Под обслуживанием может находится 0 заявок с вероятностью p, а 1 заявка с вероятностью 1-p.
Lобс |
=1(1- p) + 0× p =1- p |
|
|
|
|
|||||||||||
L = |
|
|
w |
- (1 |
- p) = |
|
|
w |
|
- w = |
|
w2 |
||||
1 |
- w |
1 |
- w |
1 |
- w |
|||||||||||
оч |
|
|
|
|
|
|||||||||||
Wоч |
= |
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
||
|
λ(1- w) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
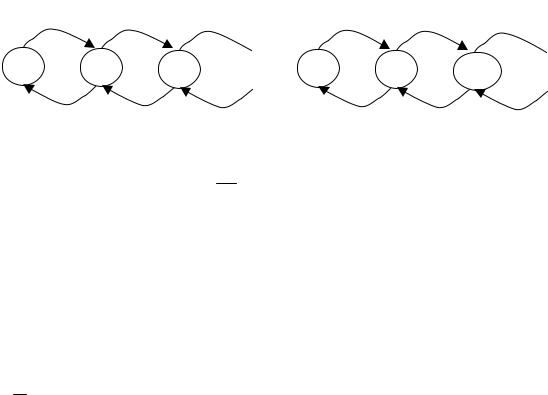
N-канальная СМО с НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ M/M/n/∞
l |
l |
|
l |
|
l |
l |
|
0 |
1 |
2 |
. . . |
n-1 |
n |
n+1 |
. . . |
|
|
||||||
m |
|
2m |
|
|
nm |
nμ |
|
Для этой системы условие стационарности: .
nμ далее остается постоянно, т.к. число каналов ограничено.
Pnλ = Pn+1nμ Pn+1 = wn Pn Pn+1λ = Pn+2nμ Pn+2 = (wn )2 Pn pn+i = (wn )i pn
Найдем суммарную вероятность для всех состояний, имеющих номера больше, чем n.
∞ |
|
|
|
|
∞ |
|
w |
|
|
|
|
|
∞ |
|
w |
|
|
|
|
w |
n+i |
|
|
|
|
|
|
|
|
|
|
|
å pn+i =å( |
)i |
pn =pn å( |
)i |
= |
|
|
p |
|
|
|
|
|
|
|
|
|||||||||||||||||
n |
n |
i |
×n! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
i=1 |
|
wn |
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||
pn |
= |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p = [1+ w + |
w2 |
|
+ |
|
w3 |
|
+...+ |
wn |
|
+ |
|
|
wn+1 |
|
|
] |
|
|
|
|
|
|
||||||||||
2 |
|
3! |
|
n! |
|
|
n!(n - w) |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Параметры системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
||||
1. |
Среднее число занятых каналов системы: |
|
|
|
|
|
μ |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
wi+1 p |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Lоч = år × Pn+r = |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n× n!(1- |
w |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r =1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||||||||||
2. |
Средняя длина очереди: |
|
|
|
|
|
|
|
|
|
|
|
|
n |
. |
|||||||||||||||||
3. |
Среднее время пребывания заявок в системе: |
Lc = Lоч + w . |
||||||||||||||||||||||||||||||
W |
= |
Lоч |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оч |
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример:

μ=0.5
2
λ=0.9
μ=0.5
λ=0.45
λ=0.45
μ=0,5 λ=0,9
Исследуем одну из одноканальных систем. 1.
w = |
|
0,45 |
= 0,9 |
|
|
|
|
|
|
||||||||||||
0,5 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p0 |
=1- w = 0,1 |
|
|
|
|
|
|
||||||||||||||
L |
|
= |
|
|
w2 |
= |
0,81 |
= 8,1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
оч |
|
|
|
1- w |
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W |
|
|
= |
Lоч |
= |
|
|
8,1 |
=18 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
оч |
|
|
|
|
|
λ |
|
|
|
|
|
0,45 |
|
|
|
|
|
|
|||
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
λ |
|
|
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|||||
w = |
|
= |
|
=1,8 |
|
|
|
|
|
|
|||||||||||
|
μ |
0,5 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p0 |
= [1+1,8 + |
|
(1,8)2 |
+ |
(1,8)3 |
]−1 |
= 0,0526 |
||||||||||||||
|
2 |
|
|
2(2 -1,8) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
L |
|
= |
|
1,83 |
×0,0526 |
= 7,67 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1,8 |
|
|
|
|
|||||
оч |
|
|
|
|
2×2!(1- |
|
)2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
7,67 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
W |
|
= |
|
= 8,52 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
оч |
|
|
|
|
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
РАСПРЕДЕЛЕНИЕ ЭРЛАНГА. МЕТОД ЭТАПОВ.
Если взять простейший поток событий, оставить в нем каждое k-ое событие, то получим поток Эрланга k- ого порядка.
t
t
f (t) = λ(λt)k−1 e−λt
(k -1)!
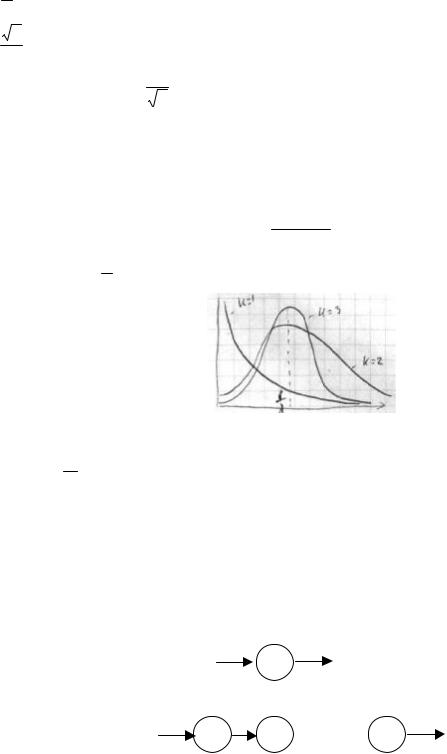
λ – интенсивность исходного потока. f(t) – функция плотности распределения.
m = λk - математическое ожидание.
σ = λk - среднеквадратичное отклонение.
Коэффициент вариации: σm = 1k
Поток Эрланга формируется таким образом, что интервалы являются суммой интервалов простейшего потока. При k→∞ фактически этот поток все ближе подходит к регулярному потоку.
Если еще одновременно с просеиванием делать масштабирование – будем получать нормированный поток Эрланга λ* = kλ .
ИНТЕНСИВНОСТЬ
Функция плотности распределения потока f *(t) = kλ(kλt)k e−λkt .
(k −1)!
Мат. ожидание: m* = λ1 для нормирования потока.
~ |
|
|
|
|
|
|
|
|
σ |
- ср. квадратичное для нормирования потока Эрланга. |
|
|
|
|
|||
~ |
|
|
|
|
|
|
|
|
σ = σ - для реального процесса это делается выбором λ и k. |
|
|
|
|||||
1 |
~ |
1 |
|
|
|
|
|
|
|
= m => λ = |
~ |
|
|
|
|
|
|
λ |
|
|
|
|
|
|
||
|
m |
|
|
|
|
|
|
|
|
|
|
~2 |
|
|
~ |
~ |
|
|
Выбирается k таким образом, чтобы k = |
m |
|
|||||
|
|
|
, тогда у потока Эрланга |
m |
и σ |
будут совпадать с |
||
|
~ |
|
||||||
|
|
|
σ |
|
|
|
|
|
реальным процессом.
Поток Эрланга обладает последействием. Интервалы становятся все больше и больше связаны друг с другом. Поэтому замена потоком Эрланга (распределением) нельзя просто заменить реальное распределение.
μ
1 |
2 |
. . . |
r |
Пока заявка не прошла все r этапов обслуживания заявка не обслуживается. Обслуживание процессов производится поэтапно. Закон распределения показательный.
Интервал времени обслуживания – он складывается из интервалов времени на каждом этапе (r). Подобрав λ, k заменяем реальное распределение распределением Эрланга с тем же m и σ.
Аналитическая модель – непрерывная Марковская модель.
Рассмотрим 2 системы: M/Er/1/∞: будем определять состояние системы, как общее число этапов
обслуживания, через которые должны пройти все заявки, находящиеся в данный момент в системе. k – заявок. Предположим в системе k заявок и заявка, которая обслуживается каналом, находящемся на i-м этапе
обслуживания.
Тогда общее количество этапов, через которые должны пройти заявки до полного их обслуживания равно: d = (k −1)r + (r −i +1)
r-i – осталось этапов для i-ой заявки.
+1 – этап, на котором обслуживается заявка.
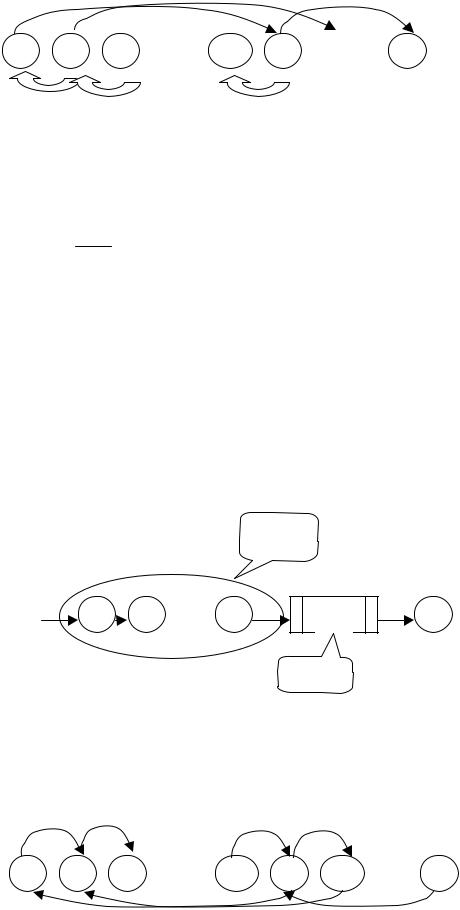
Диаграмма интенсивности переходов: |
|
λ |
λ |
0 |
1 |
2 |
. . . |
r-1 |
r |
. . . |
2r |
. . . |
|
|
|
|
|
|
|||
rμ |
|
rμ |
|
|
rμ |
|
|
|
Т.к. процесс не является процессом размножения и гибели, при составлении системы мы воспользуемся классическим положением:
åвход.поток = åвыход.поток
ìïP0λ = P1rμ
íPi (λ + μr) = Pi+1 (rμ),i =1,r -1
ïîPi (λ + rμ) = Pi+1rμ + Pi−r λ,i ³ r
Т.к. система не ограничена, то ее всегда можно ограничить из соображений точности.
От вероятностей Pi можно перейти к Pi* - вероятности нахождения i заявок в очереди (системе).
kr
Pk* = åPj
j=(k −1)r+1
СИСТЕМА СИММЕТРИЧНАЯ СИСТЕМЕ M/Er/1/∞
Er/M/1/∞
Для того, чтобы построить аналитическую модель, мы будем предполагать, что заявка поступает в системе поэтапно:
Поступ. ус-во
. . . и
rλ |
rλ |
rλ |
|
|
очередь |
Будем определять состояния в данный момент времени общим числом этапов поступления в этой системе. Если в системе уже находится k заявок, а очередная находится на i-м этапе поступления, то:
j = rk + i −1
Диаграмма интенсивности переходов для этой системы:
rλ |
|
rλ |
|
rλ |
|
rλ |
|
|
|
0 |
1 |
2 |
. . . |
r-1 |
r |
r+1 |
. . . |
2r |
. . . |
|
|
|
|
|
|
|
|||
|
μ |
|
|
μ |
|
|
μ |
|
|
Система алгебраических уравнений:

ìïP0rλ = P ×r ×μ, для _ 0 - го _ состояния
íPi rλ = Pi−1rλ + Pi+r μ,i =1,r -1 ïîPi (μ + rλ) = Pi−1rλ + Pi+r rμ,i ³ r
Pk* - вероятность нахождения в данный момент времени k заявок.
r (k +1)−1
Pk* = åPj
j=kr
Все это делается для того, чтобы свести немарковский процесс к Марковскому (который описан показательным законом распределения).
ГИППЕРЭРЛАНГОВСКОЕ РАСПРЕДЕЛЕНИЕ. Hr.
R |
k |
λ |
(k λ t)ki −1 |
|
f (t) = åPi |
i |
i |
i i |
e−λikiti |
|
(ki -1)! |
|||
i=1 |
|
|
||
Метод замены реального распределения Hr называется методом вложенных Марковских цепей. Hr – это смесь распределения Эрланга (несколько распределений с λ и k) и формирование интервала, включающего в смесь с вероятностью Pi и в результате поток становится сложным и описывается этим распределением.
НЕМАРКОВСКИЕ СМО
Это СМО, в которых потоки событий приводят к изменениям состояний системы отличны от простейших. Для таких систем встроенного математического аппарата нет, но есть частичные результаты.
1.СМО M/G/n/0
Если нуля нет, то система с отказом. G – поток общего вида.
Для систем этого вида справедливы результаты, полученные для системы M/M/n.
2.СМО M/G/1/∞
Одноканальные СМО с неограниченной очередью. Поток не является простым. Если на вход этой системы – простейший поток заявок с интенсивностью λ, а время обслуживания имеет значение t = μ1 и коэффициент
вариации ν μ = Qm , то среднее число заявок в очереди в этой системе может быть определено, как:
w2 (1+ν 2 )
Lоч = - μ
2(1 w)
w = |
1 |
|
|
|
|
μ |
|
|
|
||
|
|
|
|
||
|
|
|
w2 |
(1+ν 2 ) |
|
А среднее число заявок в системе L = |
|
μ |
+ w |
||
|
|
||||
|
|
c |
2(1- w) |
|
|
|
|
|
|
||
Используя формулу Литла можно получить средне время пребывания в очереди и в системе: wоч, wc.
3.СМО G/G/1/∞.
