
Троян_ПЕ_-_Твердотельная_электроника / Троян_ПЕ_-_Твердотельная_электроника_(УП_2006)
.pdf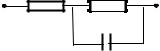
216
Rб Rш
Cш
Рис. 3.8. Эквивалентная схема диода Шоттки
Rб - омическое сопротивление базы. Данный элемент отражает падение напряжения на базе при протекании тока через прибор. Численное значение Rб при простейшей геометрии диода определяется по следующей формуле
R = r |
|
W |
, |
(3.16) |
|
||||
б |
б S |
|
||
где rб - удельное сопротивление полупроводника n - типа; |
||||
W - толщина слоя n - типа; |
|
|||
S - площадь контакта. |
системы M 2 - n+ мало |
|||
Предполагается, что сопротивление |
||||
ина величину Rб мало влияет.
Внекоторых учебниках сопротивление Rб обозначают через
Rs и называют сопротивлением растекания. Для точечного контакта сопротивление растекания можно определять по формуле
R = r |
|
1 |
, |
(3.17) |
|
||||
б |
б pа |
|
||
где а - радиус точечного контакта.
Эффект односторонней проводимости диода Шоттки отражен на эквивалентной схеме дифференциальным сопротивле-
нием R . По определению |
R = |
dU |
. Продифференцируем вы- |
||||||
|
|||||||||
|
ш |
ш |
dI |
|
|||||
|
|
|
|
|
|
|
|
|
|
ражение для тока через диод по напряжению |
|||||||||
|
dI |
= |
qIs |
exp |
qU |
. |
|
|
(3.18) |
|
|
|
|
|
|
||||
dU kT kT

217
|
I = I |
|
æ |
qU |
ö |
|
Тогда, с учетом того, что |
s |
çexp |
|
-1÷ , данное выраже- |
||
kT |
||||||
|
|
è |
ø |
ние можно представить как I + Is = Is exp qU и, взяв обратную kT
величину от (3.18), получим
Rш = |
kT |
|
. |
(3.19) |
|
q(I + Is ) |
|||||
|
|
|
|||
Видно, что при прямых включениях диода, когда через него |
|||||
течет значительный ток, Rш мало, а при обратных - |
Rш велико. |
||||
Диод Шоттки обладает емкостными свойствами. На эквива- |
|||||
лентной |
схеме емкостные свойства отражены |
емкостьюCш . |
|||
Cш - это емкость плоского конденсатора, одной из обкладок ко-
торой является металл, а второй (воображаемой) обкладкой является изменяющаяся граница ОПЗ(рис.3.9). Функцию диэлектрика в таком плоском конденсаторе выполняет ОПЗ. Тогда
Cш = ee0 S L
Cш
или с учетом (3.15)
= S |
ee0qNд |
|
2(jso ±U ). |
(3.20) |
 Ec
Ec
М  EF
EF
Ev
L
Рисунок 3.9. Структура контакта М-П, поясняющая смысл Сш
Видно, что Cш зависит от концентрации легирующей приме-
си в полупроводнике и приложенного напряжения. При прямых смещениях ширина ОПЗ уменьшается, что вызывает увеличение
|
|
|
218 |
Cш , а |
при |
обратных |
напряженияхL увеличивается и |
Cш уменьшается. Емкость Cш отражает наличие токов смещения на контакте М-П.
~
Полная величина переменного тока через диодI равна
д
сумме переменного тока, связанного с движением зарядов через
~ |
~ |
ОПЗ I и тока смещения I см . Таким образом, для протекания переменного тока через диод Шоттки существуют два параллельных канала: через Rш и Cш . Причем и сопротивление Rш и
емкость Cш зависят от величины и полярности подаваемого на диод напряжения. При обратном смещении диода Rш резко воз-
растает, и основная часть переменного тока протекает через Cш , а эквивалентную схему для переменного сигнала можно представить как последовательное соединение сопротивленияRб и
емкости Cш .
Модель диода Шоттки. Для автоматизированного моделирования и расчета электронных схем с использованием диода Шоттки используется модель диода в системе"Самрис". Любая модель предполагает совокупность схемы замещения прибора и набор математических выражений. Обычно в качестве схемы замещения используются физические эквивалентные схемы. Такие модели относятся к числу электрических функциональных моделей.
Iш = Cш dU + Uш + Iш' dt Rш
(3.21)
Iш' = Is æçexp dUm -1ö÷ è mkT ø
|
|
|
|
|
|
|
|
|
219 |
|
|
æ |
|
Uш |
ö- |
1 |
|
||||
|
|
2 |
|
|||||||
Cш |
o ç |
|
÷ |
|
|
|||||
|
o |
|
|
|||||||
= Cш ç1 + |
÷ |
(3.21) |
||||||||
|
è |
|
js |
ø |
||||||
C o |
= S |
|
ee0qNб |
|
|
|
|
|
||
ш |
|
|
|
2jso |
|
|
|
|
||
W Rб = rб S
U Б = Iш Rб
где m - коэффициент неидеальности диода Шоттки. Определяется экспериментально.
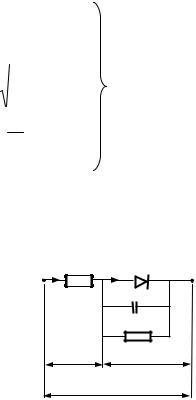
Таким образом, схема замещения (рис.3.10) и система уравнений (3.21) представляют собой модель диода Шоттки.
Iш |
I ш/ VD |
Rб |
Cш
Rш |
Uб Uш
U
Рис. 3.10. Схема замещения для модели диода Шоттки
3.7. Эффект Шоттки
Эффект Шоттки - это понижение высоты потенциального барьера Шоттки jб на контакте М-П, возникающее из-за нали-
чия сильного электрического поля и сил зеркального изображения.
Сущность эффекта проще всего рассмотреть на примере контакта металл-вакуум, а затем применить полученные выводы для контакта М-П, заменив в выражениях диэлектрическую проницаемость вакуума e = 1на диэлектрическую проницаемость полупроводника. Изначально на контакте металл-вакуум
220
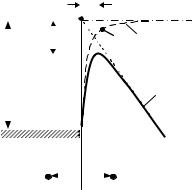
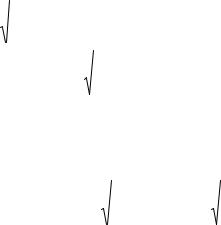
существует прямоугольный потенциальный барьерjб . Из-за наличия электрического поля у поверхности металла прямоугольный барьер OAB превращается в треугольный OAC . Учет сил зеркального изображения (при выходе электрона из металла в вакуум в металле на таком же расстоянии от поверхности образуется его зеркальное изображение, т.е. положительный заряд), определяемый законом Кулона, преобразует прямоугольный барьер OAB к виду ODB (рис.3.11).
Совместное действие сил электрического поля и учет сил зеркального изображения приводит к тому, что прямоугольный барьер OAB превращается в колоколообразный OFC . В данном случае для выхода электрона из металла в вакуум необходимо преодолеть барьер не jб , а jб - Djб .
Оценим величину Djб .
jб = [jзи (x )+jE |
(x )]= - |
|
|
|
q2 |
|
|
- qEx . |
(3.22) |
|||||
16pee |
0 x |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
Djб = 2qExm |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
А |
|
xm |
|
|
Вакуум |
В |
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Djб |
|
|
|
|
D |
j |
зи |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
jб |
|
|
|
|
F |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
М |
|
|
|
0 |
|
|
|
|
|
|
jE |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
+- e
Рис. 3.11. Контакт металла с вакуумом
jб - высота прямоугольного барьера; Djб - понижение высоты барьера j ;
jзи - потенциальный барьер с учетом сил зеркального изображения;
jЕ - потенциальный барьер с учетом сил электрического поля
221
Необходимо найти x из условия, что при x |
= x |
|
djб |
= 0 . |
||||||||||
|
|
|||||||||||||
|
|
|
|
|
m |
|
|
|
|
m |
|
dx |
||
|
|
|
|
|
|
|
|
|
|
djб |
|
|||
Тогда, |
|
диффернцируя (3.22) и приравнивая |
= 0 , получим |
|||||||||||
dx |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xm = |
|
q |
|
|
|
|
|
|
|
|
(3.23) |
|||
|
16pee0 E |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и Dj |
б = 2Exm |
= |
|
q3 E |
|
. |
|
|
(3.24) |
|||||
|
4pee |
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значение напряженности поля E не является постоянным и зависит от x . Однако, учитывая, что значение xm невелико,
можно взять значение E постоянным, равным максимальной напряженности на контакте М-П, т.е. при x = 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||
E |
= |
qNд |
L = |
qNд |
|
|
|
|
2ee0 (jso |
±U ) |
= |
|
2qNд (jso ±U ) |
|
(3.25) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(x =0) |
|
|
ee0 |
|
ee0 |
|
|
qNд |
|
|
|
|
|
|
|
|
ee0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Выражение для Djб будет иметь вид |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Djб = bш (jso ±U )1/ 4 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.26) |
||||||||||||||||
|
|
é |
|
|
q3 N |
д |
ù1/ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где bш |
= ê |
|
|
|
|
|
|
ú . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
ê8p 2 (ee |
0 |
3)ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ë |
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С учетом эффекта Шоттки ВАХ имеет вид |
|
|
|
|
|||||||||||||||||||||||||||
|
|
* 2 |
æ |
|
j |
|
|
- Dj |
ö |
æ |
|
|
qU |
ö |
|
|
|
|
|||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
||||||||||||||||||||
J = |
|
A T |
expç |
- |
|
|
|
|
|
|
б |
÷ |
×çexp kT |
-1÷ |
(3.27) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
kT |
ø |
ç |
|
|
|
÷ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
||||||||||
При прямом смещении, когда U ³ 2,3kT / q |
|
|
|
|
|||||||||||||||||||||||||||
|
|
* 2 |
æ |
|
|
jб |
ö |
æU + Djб |
ö |
|
|
|
|
||||||||||||||||||
j = |
A T |
expç |
|
- |
|
|
|
|
|
|
÷ ×expç |
|
|
|
|
|
|
÷ . |
|
|
|
(3.28) |
|||||||||
|
kT |
|
|
kT |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
è |
|
|
ø |
è |
|
|
ø |
|
|
|
|
||||||||||||||
С |
увеличением |
|
|
|
|
прямого |
напряженияDjб = bш (jso -U )1/ 4 |
||||||||||||||||||||||||
уменьшается и рост тока с напряжением происходит медленнее, чем дает теория. Это отклонение от теории можно учесть, записав ВАХ в следующем виде
222
* |
2 |
æ |
|
j |
б |
ö |
æ qU ö |
||
j = A T |
|
expç |
- |
|
|
÷ |
×expç |
|
÷ , |
|
|
|
|
||||||
|
|
è |
|
kT ø |
è nkT ø |
||||
(3.29)
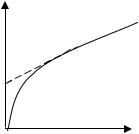
где n - коэффициент неидеальности диода Шоттки. Его опреде-
ляют по углу наклона |
,ВАХпостроенной в координатах |
|||
ln j = f (U ) как |
d (ln j) |
= |
q |
(рис.3.12). |
|
nkT |
|||
|
dU |
|
||
lnj
lnjs
|
|
|
|
|
|
U |
Рис. 3.12. Зависимость ln j от U для диодов Шоттки |
||||||
Экстраполируя отрезок прямой на рис.3.12 до U = 0 , полу- |
||||||
чают значение ln js |
|
|
|
|
|
|
ln js = ln(A*T 2 )- |
jб |
. |
(3.30) |
|||
|
||||||
|
|
|
|
kT |
|
|
Отсюда можно определить высоту барьера jб |
||||||
æ |
A*T 2 ö |
|
||||
ç |
|
|
÷ |
|
(3.31) |
|
|
|
|
||||
jб = kT lnç |
js |
÷ . |
|
|||
è |
ø |
|
Djб = bш (jso +U )-1/ 4 и |
|||
При обратном |
напряжении, когда |
|||||
уменьшение барьера Djб существенно, это приводит к росту
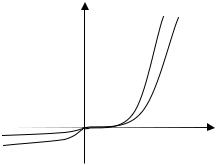
тока в обратном направлении. Таким образом, эффект Шоттки проявляется и при прямом, и при обратном напряжениях в изменении тока по сравнению с идеальной ВАХ (рис.3.13).
223
j
2
1
1 |
U |
|
2 |
Рисунок 3.13. ВАХ идеального диода (1), и с учетом эффекта Шоттки (2)
3.8. Достоинства и недостатки диодов Шоттки
Диоды Шоттки используются для изготовления дискретных приборов СВЧ-диапазона, как импульсные диоды, а также в интегральных схемах. Мощные (силовые) диоды изготавливаются обычно на основе n - кремния и имеют рабочие токи до сотен ампер и очень высокое быстродействие по сравнению с диодами на основе p - n переходов.
Главное достоинство диодов Шотткивысокое быстродействие, что связано с отсутствием эффекта накопления неосновных носителей в базе диода и не требуется времени для их рассасывания, что определяет длительность переходных процессов, а также более низкие рабочие напряжения при прямом смещении, особенно для больших токов.
К недостаткам диодов Шоттки следует отнести низкие -об ратно допустимые напряжения и большие, чем в диодах на основе p - n переходов, обратные токи. Низкие пробивные на-
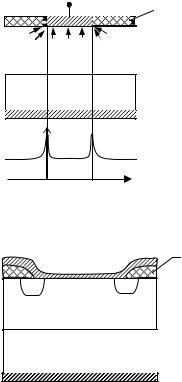
пряжения связаны с эффектом усиления напряженности электрического поля на краях контакта М-П (рис.3.14). Этот эффект устраняется, если в слое SiO2 окно имеет пологие края(как показано на рис.3.7 а) или применением охранного p - n перехода
(рис.3.15). Более высокие обратные токи обусловлены малой высотой реальных барьеров Шоттки, а также наличием туннелирования сквозь барьер при больших обратных напряжениях.
|
224 |
n |
a) |
|
|
n+ |
|
Е |
|
|
б) |
|
Х |
Рис. 3.14. Структура диода Шоттки (а) и распределение напряженности электрического поля на контакте (б)
SiO2
р |
р |
n
n+
Рисунок 3.15. Конструкция диода Шоттки с охранным p-n переходом
3.9. Омические контакты и их параметры
Основное назначение омических переходов - электрическое соединение полупроводника с токопроводящими частями полупроводникового прибора. Омические переходы играют важную роль в работе полупроводниковых, особенно интегральных, приборов, поскольку их число больше, чем выпрямляющих. Теория омических переходов разработана недостаточно хорошо, и поэтому их формирование базируется на экспериментальных данных.
Основные требования, предъявляемые к омическим переходам, следующие:
1) отсутствие инжекции из контакта в полупроводник;
225
2)минимальное падение напряжения на переходе;
3)линейность и симметричность ВАХ;
4)высокая скорость рекомбинации.
Количественно омические переходы характеризуются следующими параметрами.
1. Скорость рекомбинации. Определяется как отношение потока носителей через переход jn к избыточной концентрации носителей у перехода nгр - n0 ( nгр - концентрация носителей у
перехода, n0 |
- равновесная концентрация) S = |
|
j |
|
|
|
. |
||
nгр |
|
|||
|
|
- n0 |
||
2. Сопротивление омического перехода. Оценивается как отношение падения напряжения на переходеDU к току через переход I .
R = DU . I
Падение напряжения DU определяется как разница между падением потенциала в полупроводнике, измеренное методом зонда и падением напряжения между полупроводником и контактом. Чем меньше сопротивление R , тем лучше переход.
3. Коэффициент выпрямления KB . Определяется как от-
ношение прямого тока через переходI + к обратному I - при равных значениях прикладываемого напряжения.
I +
KB = I - U = const .
Идеальный омический переход соответствует KB = 1 .
4. Коэффициент нелинейности KH . Оценивается как от-
ношение статического сопротивления Rст к дифференциально-
му сопротивлению Rд при заданном токе I .
KH = Rст I = const Rд
