
Архив / Вычисление предела функции по определению
.docxВычисление предела функции по определению.
Задача 1.
Доказать,
что
 .
.
Решение.
Пусть
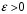 - произвольное положительное число.
- произвольное положительное число.
Составим неравенство согласно определению предела функции
(1)


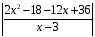 =
=
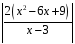 =
=
=
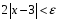 или
или
(2)
 .
.
В
качестве
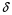 можно взять
можно взять
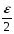 . В силу равносильности (1) и (2) из
неравенства
. В силу равносильности (1) и (2) из
неравенства
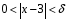 будет следовать неравенство (1).
будет следовать неравенство (1).
Задача 2.
Доказать,
что последовательность с общим членом
 имеет предел, равный 1.
имеет предел, равный 1.
Решение.
Выберем
произвольное положительное число
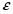 и покажем, что для него можно определить
такое натуральное число
и покажем, что для него можно определить
такое натуральное число
 ,
что для всех номеров
,
что для всех номеров
 будет выполняться неравенство
будет выполняться неравенство
 :
:

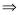
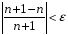
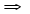
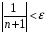 .
Выражение под знаком модуля положительно,
поэтому последнее неравенство имеет
вид
.
Выражение под знаком модуля положительно,
поэтому последнее неравенство имеет
вид

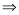
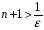
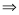
 .
.
Следовательно,
если номер
 будет больше, чем
будет больше, чем
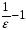 ,
то неравенство
,
то неравенство
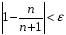 будет
выполняться. При этом за число
будет
выполняться. При этом за число
 принимаем
наибольшее целое число, содержащееся
в числе
принимаем
наибольшее целое число, содержащееся
в числе
 .
.
