
Архив / Замечательные пределы
.docx
Предел
функции
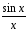 при
при
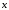
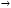 0
(Первый
замечательный предел).
0
(Первый
замечательный предел).
Для
функции
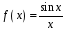 в
точке
в
точке
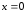 имеет
место неопределенность
имеет
место неопределенность
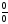 .
Найдем предел этой функции при
.
Найдем предел этой функции при

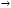 0.
Будем использовать признак существования
предела (а).
0.
Будем использовать признак существования
предела (а).
Рассмотрим
окружность радиуса
 .
Обозначим центральный угол MOB
через
.
Обозначим центральный угол MOB
через
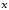 ,
при
этом 0
<
,
при
этом 0
<
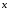 <
<
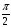 .
В
результате получаем оценку для площадей:
.
В
результате получаем оценку для площадей:




C
Площадь ∆MOA
< площади сектора MOA
< площади ∆COA.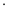


M
Площадь ∆MOA
=
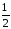 OA
OA
 MB
=
MB
=

 1
1
 MB
=
MB
=
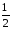
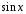 .
.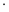
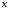

O
B
A
Площадь сектора MOA
=
 OA
OA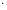
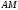 =
=
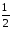
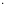 1
1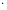
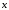 .
.

Площадь
∆COA
=
 OA
OA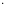 AC
=
AC
=
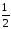
 1
1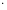
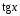 =
=
 .
.
Из
оценки для площадей следует оценка для
функций:
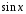 <
<
 <
<
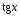 .
.
Разделим
все последнего соотношения на
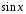 :
:
1
<
 <
<
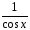 или
или
 <
<
 < 1.
< 1.
Это
неравенство справедливо в предположении,
что
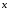 >
0. Но в силу четности:
>
0. Но в силу четности:
 =
=
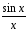 и
и
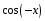 =
=
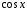 ,
заключаем, что оно верно и при
,
заключаем, что оно верно и при
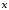 < 0.
< 0.
С
учетом того, что
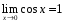 ,
,
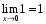 ,
переменная
,
переменная
 заключена между двумя величинами,
имеющими один и тот же предел, равный
1.
По признаку существования предела
заключена между двумя величинами,
имеющими один и тот же предел, равный
1.
По признаку существования предела
 =
1.
=
1.
Второй
замечательный предел
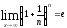 .
.
Для
последовательности с общим членом

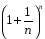 при
при
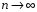 имеет
место неопределенность
имеет
место неопределенность
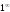 ,
раскрывая которую получаем предел,
заключенный между числами 2 и 3 .
,
раскрывая которую получаем предел,
заключенный между числами 2 и 3 .
Доказательство основано на признаке существования предела (б). Поэтому требуется установить, что члены последовательности монотонно возрастают, и последовательность ограничена сверху.
Для доказательства монотонности используем формулу бинома Ньютона, и получаем для общего члена последовательности выражение:
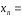
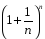 =
1 +
=
1 +

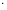
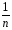 +
+

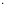
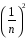 +
+


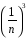 +
+
 +
+
+

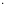
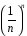
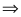

 =
1 + 1 +
=
1 + 1 +
 +
+
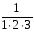

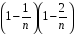 +
+
 +
+
+
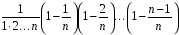 .
.

Из
последнего равенства видно, что каждый
последующий член этой последовательности
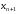 по сравнению с предыдущим
по сравнению с предыдущим
 содержит еще одно положительное
слагаемое. Кроме того, каждое слагаемое
в выражении для
содержит еще одно положительное
слагаемое. Кроме того, каждое слагаемое
в выражении для
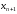 больше соответствующего слагаемого в
выражении
больше соответствующего слагаемого в
выражении
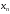 :
:
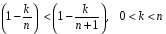 .
Следовательно,
.
Следовательно,
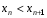 ,
то есть последовательность является
возрастающей.
,
то есть последовательность является
возрастающей.
Для доказательства ограниченности сверху данной последовательности заметим, что каждое выражение в скобках в соотношении (*) меньше единицы:
 ;
;
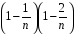 < 1 ….. . Поэтому для общего члена
последовательности получаем оценку:
< 1 ….. . Поэтому для общего члена
последовательности получаем оценку:

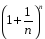 <
1 + 1 +
<
1 + 1 +
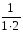 +
+
 +
+
 +
+
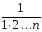 ;
;
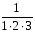 <
<
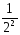 ,
,
 <
<
 ,
,
 ,
,
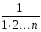 <
<
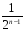 ;
;
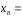
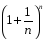 <
1 + 1 +
<
1 + 1 +
 +
+
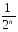 +
+
 +
+
 .
.
Выражение
1 +
 +
+
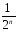 +
+
 +
+
 представляет
сумму членов геометрической прогрессии
со знаменателем q
=
представляет
сумму членов геометрической прогрессии
со знаменателем q
=
 и
первым членом 1. Используя формулу
суммы геометрической прогрессии,
приходим к неравенству:
и
первым членом 1. Используя формулу
суммы геометрической прогрессии,
приходим к неравенству:

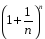 <
1 +
<
1 +
 = 1 +
= 1 +
 < 3.
< 3.
С
учетом неравенства
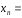

 2
( следует из (*)) получаем оценку
2
( следует из (*)) получаем оценку
2
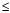
 < 3.
< 3.
По
признаку существования предела, если
последовательность монотонно возрастает
и ограничена, то она имеет предел. Этот
предел обозначается буквой
 :
:
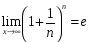 .
.
Число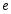 -
иррациональное число, равное
-
иррациональное число, равное
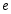 =
2,7182818284…
=
2,7182818284…
