Московский Технический Университет Связи и Информатики

Лабораторная работа №6

Алгоритмы решения задачи одномерной оптимизации.

Задание:

1. Решить задачу оптимизации функции с точностью методом дихотомии. Результаты записать в таблицу.

2. Вычислить число итераций, необходимых, чтобы локализовать точку минимума с точностью E.

3. Методом золотого сечения решить задачу оптимизации (три итерации).

4. Определить длину конечного отрезка, содержащего точку минимума.

5. Вычислить теоретическую точность оптимизации. Сравнить с результатом, полученным в п. 4.

6. Проиллюстрировать графически решение задачи.

Исследование задания:

Определим отрезок унимодальности функции f(x). Практический критерий унимодальности функции требует непрерывности функции и выполнения условия при или неубывания .

Для проверки унимодальности вычислим

Функция при

Таблица 1

X	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4	4,5
	-1,025	-0,686	-0,321	0,066	0,469	0,884	1,305	1,727	2,143	2,549	2,938

На отрезке [3,5;4,5] функция возрастает, (), следовательно, функция y=f(x) унимодальная на этом отрезке.

Отрезок [3,5;4,5] – начальный отрезок неопределенности.

График функции

Решение задачи оптимизации методом дихотомии.

N+1	A	B	F(A)	F(B)	A-B
1	3.50000	4,50000	-2,819585	-1,910642	1,00000
2	3.50000	4,00003	-2,819585	-2,874467	0,50003
3	3,74999	4,00003	-2,967111	-2,874467	0,25004
4	3,74999	3,87503	-2,967111	-2,952520	0,12504
5	3,74999	3,81253	-2,967111	-2,967584	0,06255
6	3,78124	3,81253	-2,969266	-2,967584	0,03130
7	3,78124	3,79691	-2,969266	-2,968907	0,01567
8	3,78124	3,78910	-2,969266	-2,969207	0,00786
9	3,78124	3,78519	-2,969266	-2,969267	0,00396
10	3,78319	3,78519	-2,969274	-2,969267	0,00200
11	3,78319	3,78422	-2,969274	-2,969272	0,00103
12	3,78319	3,78373	-2,969274	-2,969274	0,00054
13	3,78319	3,78348	-2,969274	-2,969274	0,00029
14	3,78319	3,78336	-2,969274	-2,969274	0,00017
15	3,78319	3,78330	-2,969274	-2,969274	0,00011
16	3,78322	3,78330	-2,969270	-2,969274	0,00008

,

Определим число итераций N, необходимых для локализации точки минимума с точностью , из условия, что длина конечного отрезка неопределенности не превышает заданной точности.

- длина конечного отрезка после N итераций для метода дихотомии.

< E - точность достигнута, N>=15.

Решение задачи оптимизации методом золотого сечения:

N+1	a	b	f(a)	f(b)	b-a
1	3,5	4,5	-2,81958	-1,91064	1
2	3,5	4,11803	-2,81958	-2,74084	0,61803
3	3,5	3,88197	-2,81958	-2,94988	0,38197
4	3,64590	3,88197	-2,93304	-2,94988	0,23607

Определим длину отрезка (теоретическая величина погрешности), содержащую точку минимума, после 3-х итераций, пользуясь формулой , . Расчетная длина

Графическая иллюстрация:

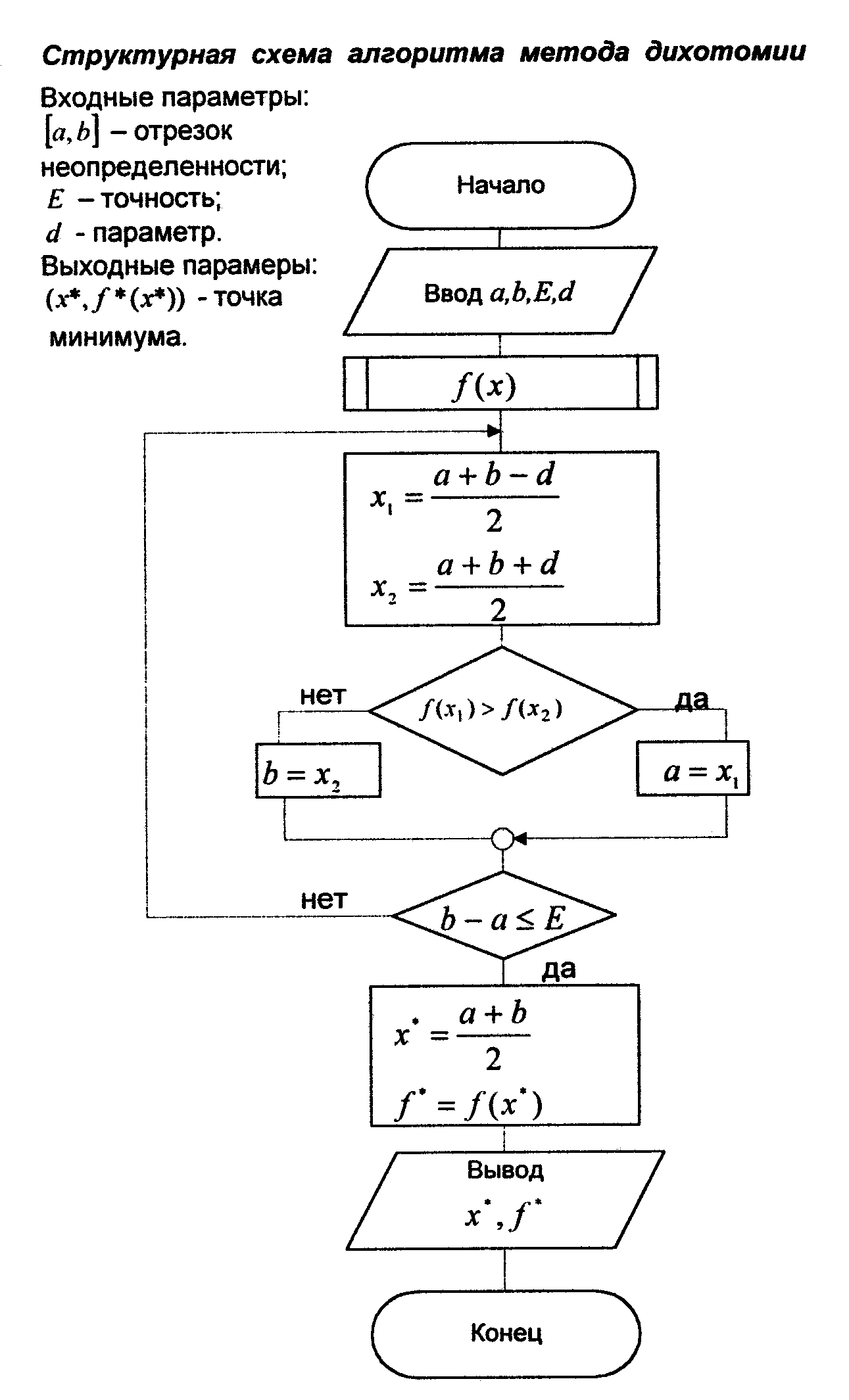
Программа метода дихотомии:

Program Dihotomia;

Uses

Crt;

Function F(X:Real):Real;

Begin

F:=sin(x-1)-x*cos(x+3);

End;

Var

A,B,D,E:Real;

N:Byte;

Begin

ClrScr;

d:=0.00005;

A:=3.5;

E:=0.0001;

B:=4.5;

N:=1;

WriteLn('N+1 A B F(A) F(B) B-A');

While (B-A)>=E Do

Begin

Write(N:2,' ');

Write(A:0:5,' ');

Write(B:0:5,' ');

Write(F(A):0:6,' ');

Write(F(B):0:6,' ');

Write(B-A:0:5,' ');

WriteLn;

If F((A+B-D)/2)<F((A+B+D)/2) Then

B:=(A+B+d)/2

Else

A:=(A+B-d)/2;

Inc(N);

End;

Write(N:2,' ');

Write(A:0:5,' ');

Write(B:0:5,' ');

Write(F(A):0:5,' ');

Write(F(B):0:5,' ');

Write(B-A:0:5,' ');

WriteLn;

Write('X=',(A+B)/2:0:6,' ','F(X)=',F((A+B)/2):0:5);

ReadLn;

End.