Контрольні запитання

1.Що таке регресія, коефіцієнт регресії?

2.Що характеризує коефіцієнт прямолінійної регресії і які можливості застосування цього показника у зоотехнічній практиці?

Лабораторна робота №8

Тема: “Розрахунок коефіцієнта кореляції між альтернативними ознаками (r_а)”

Мета заняття: оволодіти методикою розрахунку та набути практичних навичок застосування коефіцієнта кореляції між альтернативними ознаками.

Теоретичні положення

Взаємозв’язок між альтернативними ознаками визначається мірою поєднання кожного з двох можливих етапів ознаки у двох взаємопов’язаних групах особин і виражається коефіцієнтом кореляції між ними (r_a). Він особливо зручний при аналізі генетичних даних (зв’язок між мастю батьків і нащадків, забарвленням пір’я у курчат та статтю, стійкістю до окремих захворювань батьків та їх нащадків тощо).

Для розрахунку коефіцієнта кореляції між альтернативними ознаками будують чотирипільні кореляційні гратки, куди заносять дані спостережень за кожним членом вибірки. Найчастіше для розрахунку r_a використовують таку формулу:

,

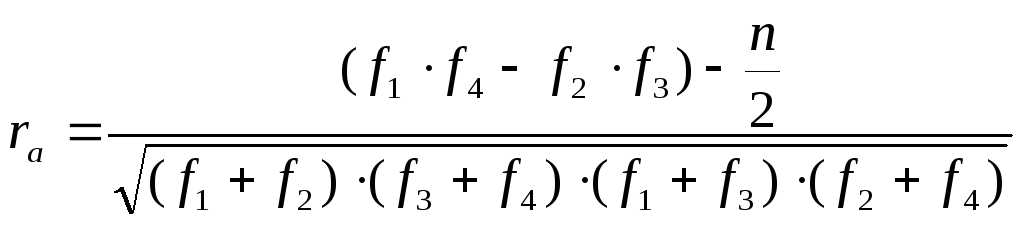де f₁, f₂, f₃, f₄ – частоти в кожному полі кореляційних граток,

n – загальна кількість спостережень.

Величина r_a може знаходитись в межах від –1,0 до +1,0.

Методика виконання типового завдання

Приклад. У стаді великої рогатої худоби при обстеженні 461 корови встановлено, що з них 391 голів були здоровими, а 70 хворими на лейкоз. Серед їх 160 дочок співвідношення між хворими та здоровими було відповідно 46 і 114 голів. Розрахувати r_a, S_ra, t_ra між частотою захворювання матерів та їх дочок. Форма запису така:

1. Кореляційні гратки частоти захворювання на лейкоз матерів (х) та їх дочок (у)

Група	Матері	Дочки	Всього
Здорові	f1 391	f2 114	f1 + f2 505
Хворі	f3 70	f4 46	f3 + f4 116
Всього	f1 + f3 461	f2+f4 160	n=f1+f2+f3 +f4=621

Користуючись вище наведеною формулою, розраховуємо :

1) ;

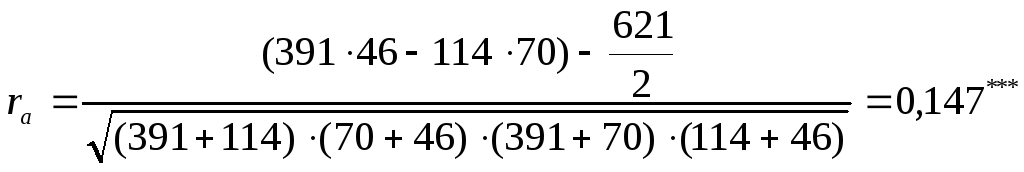2)

3) ;

4) v=n-2=621-2=619; t_st=2-2,6-3,3; P>0,999.

Висновок: між частотою захворювання на лейкоз корів (матерів та їх дочок) існує слабкий позитивний зв’язок. Дочки від хворих корів частіше хворіють на лейкоз, ніж від здорових. Коефіцієнт кореляції (r_a=0,147) достовірний з імовірністю P>0,999.

Контрольні запитання

1. Які ознаки називаються альтернативними?

2. За якою формулою визначають коефіцієнт кореляції між альтернативними ознаками?

3. Які гратки будують для розрахунку даного коефіцієнта?

Лабораторна робота №9

Тема: “Застосування в селекції та розрахунок коефіцієнта

Рангової кореляції (rs)”

Мета заняття: оволодіти методикою розрахунку та набути практичних навичок застосування коефіцієнта рангової кореляції.

Теоретичні положення

Коефіцієнт рангової кореляції розраховують для ознак, які не можна або немає необхідності виміряти, але за якими особини можуть бути розміщені за наростаючим чи спадаючим ступенем їх вираженості.

Групу особин, розміщених за ступенем вираженості ознаки від максимального значення до мінімального або навпаки, називають ранжированим рядом, а процес формування такого ряду називаютьранжируванням.Порядковий номер особини в ранжированому ряді визначає їїранг(1, 2, 3 ...). Якщо фактична абсолютна величина ознаки у декількох особин вибірки однакова, то їх нумерують підряд і беруть середнє із суми цих рангів.

В обробку включаються не абсолютні величини варіюючої ознаки, а їх ранги, зайняті членами сукупності за кожною із корелюючих ознак. Метод запропоновано Спірменом, тому часто в літературі коефіцієнт рангової кореляції називають коефіцієнтом Спірмена.

Його розраховують за формулою: ,

де х – ранги за х-ознакою;

у – ранги за у-ознакою;

х-у – різниця рангів;

n– число пар рангів, або об’єм вибірки.

Різницю рангів (х-у) можна замінити літерою d, і тоді формула набуває більш спрощеного вигляду:,

де Σd²– сума квадратів різниці між парними рангами.

Оцінка достовірності коефіцієнта рангової кореляції дещо ускладнена, бо розподіл рангових коефіцієнтів може ще більше відхилятись від нормального, ніж розподіл простих коефіцієнтів кореляції. Її здійснюють, користуючись даними додатку 2.