Контрольні запитання

1. За якими формулами і в якій послідовності розраховується коефіцієнт кореляції для малих вибірок?

2. У чому особливість методики розрахунку коефіцієнта кореляції для малих та великих вибірок?

3. Яка характеристика сили і напрямку зв'язку між ознаками?

4. Як визначити критерій достовірності коефіцієнта кореляції?

Лабораторна робота №7

Тема: “Застосування в селекції та розрахунок коефіцієнта прямолінійної регресії (R) для великих та малих вибірок”

Мета заняття: освоїти методику розрахунку коефіцієнта прямолінійної регресії та зробити висновок про використання його у селекції.

Теоретичні положення

Коефіцієнт прямолінійної регресії (R), який також належить до показників зв’язку, характеризує його динаміку та кількісно конкретизує взаємозв’язок між х та у ознаками. Він показує, на скільки в середньому змінюється одна ознака при зміні іншої, взаємопов’язаної з нею на одиницю виміру, і навпаки.

Знаючи коефіцієнт регресії однієї ознаки щодо іншої, взаємопов’язаної з нею, можна прогнозувати розвиток величини цієї ознаки, безпосередньо її не вивчаючи.

Наприклад, користуючись регресійним аналізом, можна визначити живу масу тварин (без зважування) за промірами висоти в холці або за обхватом грудей.

Коефіцієнт регресії в кожній конкретній вибірці має два значення: R_x/y та R_y/x і розраховується для великих вибірок за формулами:

При розрахунку R береться повна σ варіаційного ряду, тому сигму, одержану при розрахунку коефіцієнта кореляції необхідно помножити на величину класового проміжку:

σ_х=σ_х·k_х; σ_y=σ_y·k_у.

При розрахунку коефіцієнта регресії для малої вибірки використовують формули:

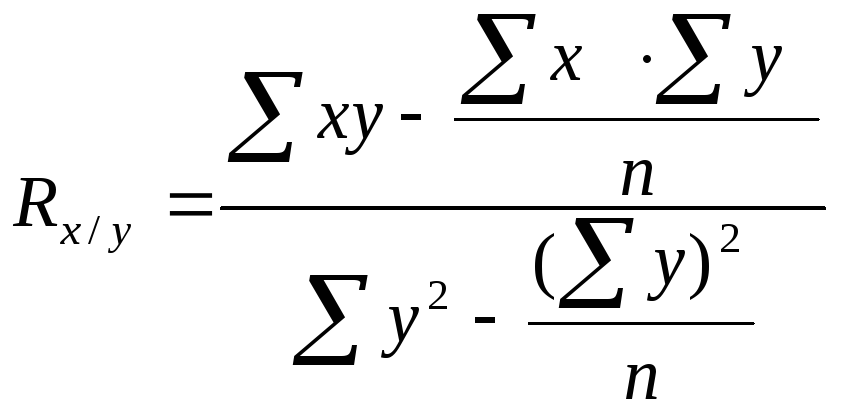
або .

Коефіцієнт регресії має велике значення в генетичних і в селекційних дослідженнях. Найбільш широко його використовують для визначення коефіцієнта успадковуваності (h²) для кількісних ознак (наприклад, визначають регресію надою дочок за показниками надою їх матерів).

Методика виконання типового завдання

1. Використовуючи дані лабораторної роботи №5 визначаємо коефіцієнт прямолінійної регресії. Вихідні дані: r=0,62, σ_х=1,22 кг, k_х=25 кг, σ_у=1,17 см, k_у=4 см.

При розрахунку Rбереться повна σ варіаційного ряду, тому сигму, одержану при розрахунку коефіцієнта кореляції, необхідно помножити на величину класового проміжку:

σ_х =1,22·25=30,5 кг , σ_у=1,17·4=4,68 см.

; .

Висновок: при зміні висоти в холці свиноматок на 1 см їх жива маса зміниться в середньому на 4,04 кг, а при зміні живої маси свиноматок на 1 кг їх висота зміниться в середньому на 0,1 см.

2. Використовуючи дані лабораторної роботи №6 приклад №1 визначаємо коефіцієнт регресії для малої вибірки:

, .

, .

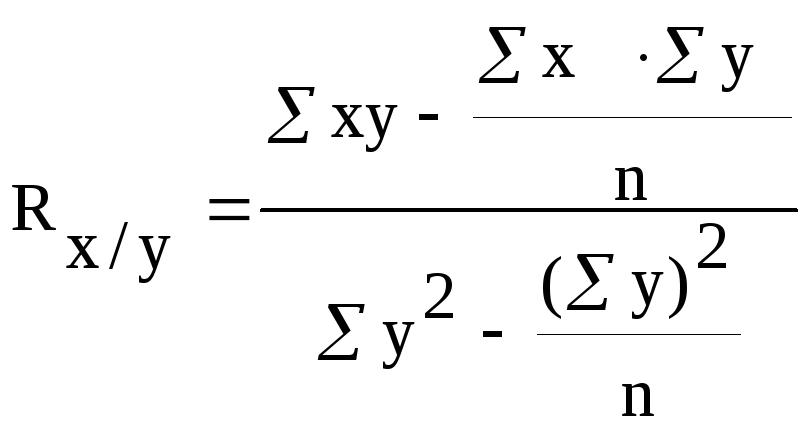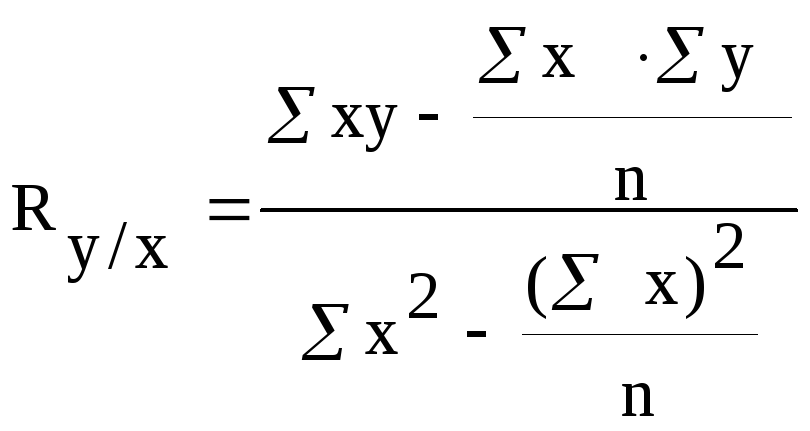Висновок: при зміні вмісту жиру (х) на 1% вміст білку зміниться на 2,1%, а при зміні вмісту білку (у) на 1% вміст жиру зміниться в середньому на 0,43%.

3. Використовуючи дані лабораторної роботи №6 приклад №3 визначаємо коефіцієнт регресії за такими формулами:

, .

, .

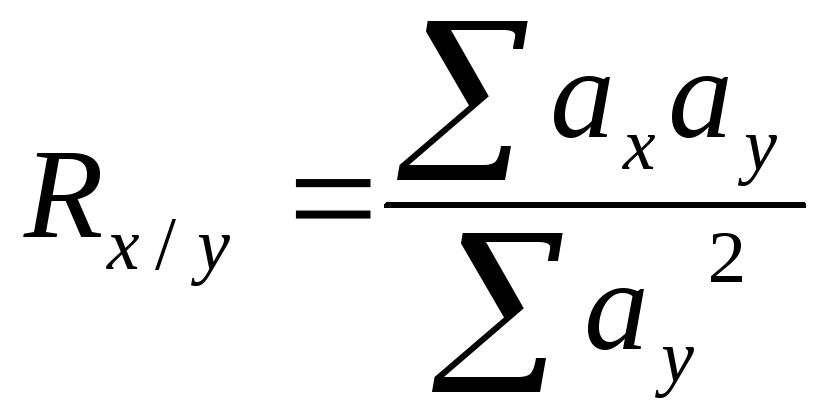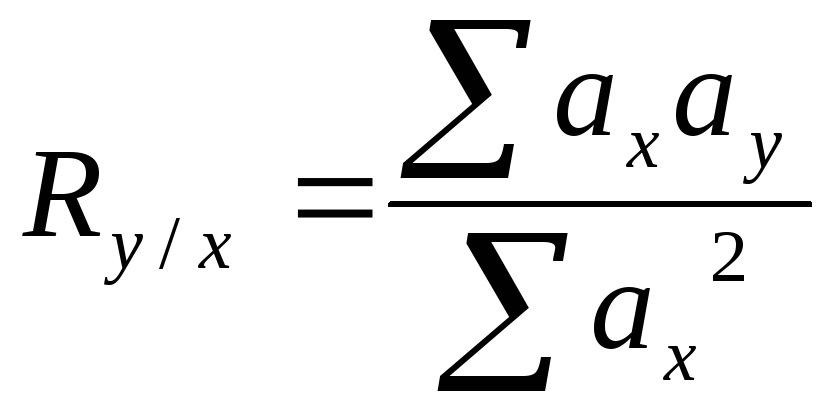Висновок: при зміні висоти в холці свиноматок на 1 см жива маса зміниться в середньому на 8 кг, а при зміні живої маси на 1 кг їх висота зміниться в середньому на 0,1 см.