Контрольні запитання
1. На що вказує коефіцієнт кореляції? Як ви розумієте функціональні та корелятивні типи зв’язку і для яких явищ вони характерні?
2. Які типи зв’язку між ознаками можуть бути за формою, за напрямом та за силою?
3. Яким показником виражається зв’язок між ознаками і в яких межах він може коливатись?
4. Що таке кореляційні гратки і як вони складаються?
5. За якою формулою і в якій послідовності розраховується коефіцієнт кореляції для великих вибірок?
6. Чим відрізняється σ варіаційного ряду від σ кореляційних граток?
7. За якою формулою визначають вірогідність коефіцієнта кореляції та його помилку?
Лабораторна робота №6
Тема: “Розрахунок r, Sr, tr для малих вибірок”
Мета заняття: освоїти методи розрахунку коефіцієнта фенотипової кореляції між кількісними ознаками при малих вибірках та набути практичних навиків використання показників кореляції в селекції тварин.
Теоретичні положення
На відмінну від великої вибірки при малому числі спостережень кореляційні гратки не складаються.
Запропоновано велику кількість формул для розрахунку коефіцієнта кореляції при n<30. У біологічних дослідженнях найчастіше використовуються такі формули:
(1) та
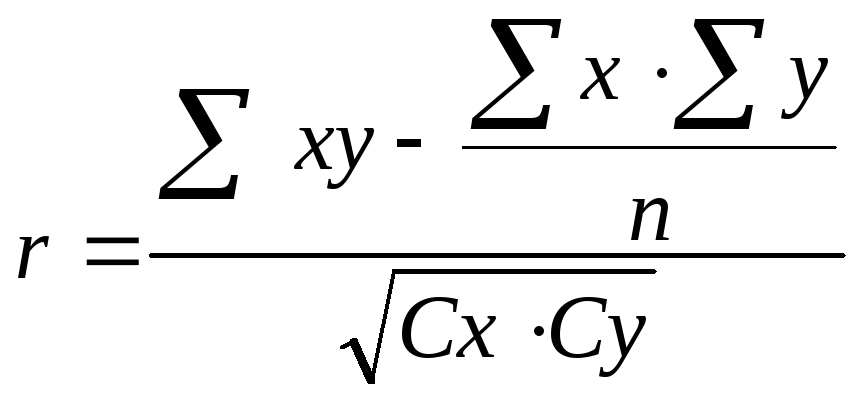(2),
де Сх – сума квадратів центральних відхилень за ознакою х;
Су – сума квадратів центральних відхилень за ознакою у;
Сd – сума квадратів центральних відхилень для різниці х-у;
n – об’єм вибірки.
Перша формула застосовується для роботи як з малозначними, так і з багатозначними варіантами. Друга формула, як правило, застосовується при роботі з вибірками, які складені тільки з малозначних варіант.
Сума квадратів центральних відхилень у випадку роботи із малозначними варіантами розраховується за такими формулами:
;
;
Для багатозначних варіант сума квадратів центральних відхилень розраховується за формулами:
;
;
Помилку коефіцієнта кореляції (Sr) в малочисельній вибірці розраховують за формулою:
.
Для розрахунку критерію вірогідності коефіцієнта кореляції використовується формула:
.
Методика виконання типового завдання
Приклад №1. Розрахувати величину зв’язку r, його помилку Sr, критерій достовірності tr між вмістом жиру (х) і білка (у) в молоці 10 корів джерсейської породи (табл.1).
1.Форма запису для розрахунку коефіцієнта кореляції між вмістом жиру і білка
в молоці корів (малозначні варіанти), %
|
№ п/п |
х |
у |
ху |
х2 |
у2 |
|
1 |
4,5 |
3,6 |
16,2 |
20,25 |
12,96 |
|
2 |
4,0 |
3,2 |
12,8 |
16,00 |
10,24 |
|
3 |
4,6 |
3,5 |
16,1 |
21,16 |
12,25 |
|
4 |
5,0 |
3,6 |
18,0 |
25,00 |
12,96 |
|
5 |
4,0 |
3,3 |
13,2 |
16,00 |
10,89 |
|
6 |
4,1 |
3,3 |
13,53 |
16,81 |
10,89 |
|
7 |
4,5 |
3,5 |
15,75 |
20,25 |
12,25 |
|
8 |
4,8 |
3,6 |
17,28 |
23,04 |
12,96 |
|
9 |
4,9 |
3,7 |
18,13 |
24,01 |
13,69 |
|
10 |
5,2 |
3,8 |
19,76 |
27,04 |
14,44 |
|
|
Σх=45,6 |
Σу=35,1 |
Σху=160,75 |
Σх2=209,56 |
Σу2=123,53 |
Об’єм вибірки становить 10 варіант. Після проведення необхідних математичних розрахунків одержуємо підсумковий ряд цифр у всіх стовпчиках, які використовуються для розрахунків окремих елементів формули коефіцієнта кореляції.
Сума квадратів центральних відхилень становить:
Звідси
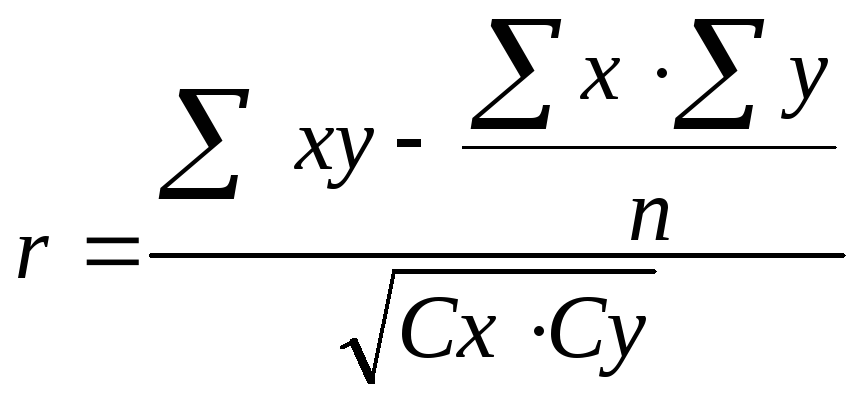r=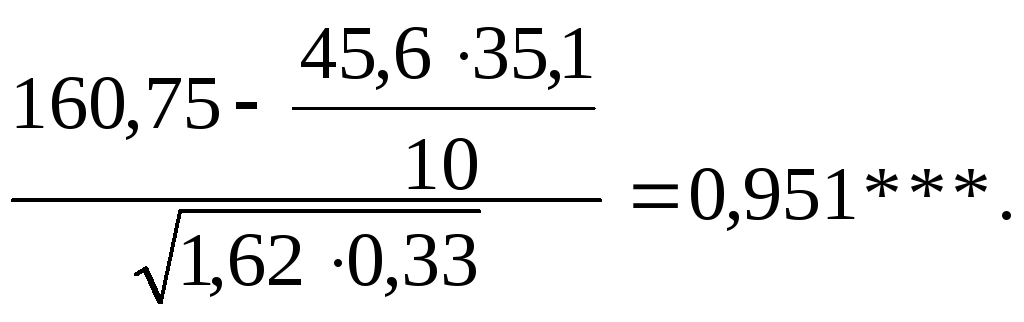
Аналогічне значення
коефіцієнта кореляції можна одержати
використавши формулу:
.
При цьому необхідно додати до таблиці
1 колонки для розрахунку значень:d=x-y
іd2
для визначення Cd.
Розрахований коефіцієнт фенотипової кореляції (r=0,951) вказує на існування позитивного і тісного зв’язку між вмістом жиру і білка в молоці корів. Така кореляція між ознаками дозволяє проводити селекцію, тобто відбір корів по жирномолочності буде приводити і до підвищення вмісту білка в молоці.
Але остаточно судити про силу та напрямок зв’язку між ознаками можна лише тоді, коли підтверджена вірогідність (tr) розрахованого коефіцієнта кореляції, яка залежить від об’єму вибірки і величини його помилки (Sr).
Користуючись формулою розраховуємо помилку коефіцієнта кореляції (Sr):
=
%.
Визначаємо критерій вірогідності коефіцієнта кореляції (tr):
=
.
Знаходимо число ступенів свободи:
v=n-2=10-2=8.
За таблицею Стьюдента при v=8 tst=2,3; 3,4; 5,0.
Порівнюючи розраховане значення tr із стандартним tst, робимо висновок, що розрахований коефіцієнт кореляції достовірний з імовірністю Р≥0,999.
Приклад №2. При розрахунку коефіцієнта кореляції для вибірок, складених із багатозначних варіант, відмінність лише у тому, що будують дещо іншу форму запису розрахунків і за іншими формулами розраховують суми квадратів центральних відхилень (Сх, Су, Сd).