Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет геодезии и картографии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Известия вузов Геодезия и аэрофтосъемка №6

.pdf

Скачиваний:

Добавлен:

02.05.2015

Размер:

3.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

геодезическое приборостроение

(рыскание) считается положительным при повороте с севера на восток, дифферент (килевая качка) положителен когда нос корабля поднят вверх относительно плоскости OXZ, крен (бортовая качка) — при повороте в сторону правого борта. Отсчёты углов оси А1 возрастают при повороте вращающейся части в сторону правого борта корабля. Отсчёты углов по оси А2 положительны при повороте оптических осей телескопов от нулевого значения угла через зенит в направлении от носа к корме корабля. Диапазон предельных углов поворота:

по оси А1 …………±100°; по оси А2 …………от +95 до –70°.

Биения оси А1. Рассмотрим влияние угловых биений оси А1 на измерения. Биения будем задавать в общем виде, т.е. ось А1 может быть смещенавлюбойплоскости,проходящейчерез её идеальное положение. Эта погрешность может быть выражена через два последовательных поворота вокруг оси Y′ и Z″ (рис. 3), т.е.

матричное преобразование TZ′′(ε1) TY ′(ε2). Далее вокруг полученных смещённых осей монтировки осуществляются повороты на углы α1 и α2, что записывается следующим образом:

	Y'(ИСКМ)
			Y1(ВСК)
		30o	(ПСКМ)			Z1(Z')
	X2		(ПСКМ)			Z1(Z')
	X2		Y2
X1	αZ					XОi YОi(СКО)
	αZ		αZ Z (A )
X'(A1)		Ц	αX	2	2			ZОi
			1
	αX		1				ЦОi
	αX						ЦОi

ХО

A2(Z2)

30° A1(X')

Направление на нос корабля

Рис. 1. Опорно-поворотное устройство (ОПУ) оптического комплекса:

1 — основание; 2 — двигатели моментные; 3 — оптический блок ОБ2; 4 — датчики угловые;

5 — объективы; 6 — оптический блок ОБ1; 7 — опорный блок

YО

ZО(КСК)

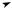Z(МСК)

ЦО,Ц

Рис.2. Системы координат корабля

известия высших учебных заведений. геодезия и аэрофотосъемка, № 6, 2010

X ′

TZ * (α2)TX ′′(α1)TZ ′′(ε1)TY ′(ε2) Y′ = Aнепр , (1)

Z′

где Z* — ось, полученная поворотом оси Z″ вокруг X″ на угол α1; Aнепр — вектор координат «неправильного» направления с учётом биений.

Далее, задавая Aнепр единичным и равным 1 , т.е. определяющим оптическую ось объекти-

ва, из (1) получим:

′

′ = TZ * (α2)TX ′′(α1)TZ ′′(ε1)TY ′(ε2) −1 Aнепр. (2) ′

Из выражения (2) для координат X′, Y′, Z′ легко получить тангенс угла поворота вокруг оси А1 с учётом введённых погрешностей биения:

tg(α1 + ∆α1) = Z′′(α1,α2,ε1,ε2),

Y (α1,α2,ε1,ε2 )

где Δα1 — погрешность поворота вокруг оси А1, вызванная её угловыми биениями.

С другой стороны, данный тангенс по известной формуле тангенса суммы углов можно за-

писать следующим образом: tg(α1 + ∆α1) = tgα1 + tg∆α1 ,т.е. получаем уравнение: 1− tgα1 tg∆α1

	tgα1 + tg∆α1 =		Z′(α1,α2,ε1,ε2 ).
	1− tgα1 tg∆α1		Y′(α1,α2,ε1,ε2)

Далее осуществлялись тригонометрические преобразования данного уравнения, где кро-

ме всего прочего учитывалось, что ввиду малости углов ε1, ε2 выполняются равенства cos ε1 ≈ 1;

cos ε2 ≈ 1; sin ε1≈ tg ε1 ≈ ε; sin ε2≈ tg ε2 ≈ ε. В итоге была получена следующая формула для Δα1:

ε1 tgα1 tgα2 +ε2 tgα2 +ε1ε2 cosα1

(3)

tg∆α1 =

tgα tgα

−ε tgα

+ε ε

sinα

cosα

1 2

Также, учитывая (2), можно записать выра-

ε2

жение для синуса угла поворота вокруг оси А2

с учётом введённых биений:

sin(α2 + ∆α2 ) = −X ′(α1,α2,ε1,ε2 ),

где Δα2

— погрешность поворота вокруг оси А2,

вызванная угловыми биениями оси А1.

Откуда после тригонометрических преоб-

θε1

разований и, учитывая, что

sin(α2 + ∆α2 ) = sinα2 cos∆α2 +cosα2 sin∆α2

≈

εA1

ε2

≈ sinα2 +cosα2∆α2,

получим:

X'(A1)

∆α2 = ε1 cosα1 −ε2 sinα1.

(4)

Рис. 3. Биения оси А1

(ось А1 для наглядности направлена вниз)

геодезическое приборостроение

Отдельные ортогональные составляющие биения ε1 и ε2 можно задать через амплитуду биения оси А1 — εA1 и угол биения θ1 относительно вертикальной плоскости OX′Y′:

				ε1	= εA cosθ1; ε2					= εA	sinθ1.													(5)
					1					1
Подставляя (5) в (3) имеем:
		ε2	cosθ sinθ cosα +ε					A	cosθ tgα tgα						2	+ε	A	sinθ tgα				2
tg∆α1 =		A		1	1	1		A		1		1			2		A		1			2	.	(6)
		1						1									1
	ε2	cos	θ sinθ sinα +ε			A	sinθ tgα tgα					2	−ε	A		cosθ tgα			2	+		1
	ε2	cos	θ sinθ sinα +ε				sinθ tgα tgα						−ε			cosθ tgα				+
	A		1	1	1				1	1								1			cosα1
1						1									1

Определим теперь математическое ожидание и дисперсию погрешности Δα1, вызванной биением оси А1.

Известно [2, 3], что угловое биение ε, вызванное эксцентриситетом, подчиняется арксинусоидальному закону распределения вероятностей (рис. 4):

p(ε) =	1			,

	π ε2		−ε2
		m

где εm — амплитуда углового биения; p(ε) — плотность вероятности.

Значение угла биения θ1 относительно вертикальной плоскости OX′Y′ в (5) может принимать любое значение от –π/2 до π/2 и для распределения вероятностей угла θ1 выберем равномерный закон.

Таким образом, (6) представляет собой функцию случайных величин с известными законами распределения вероятностей, поэтому можно записать следующие выражения для математического ожидания и дисперсии погрешности Δα1 вследствие биения оси А1:

π 2

εm

cosθ1 sinθ1 cosα1 +εcosθ1 tgα1 tgα2

+εsinθ1 tgα2

M1(1) (α1

,α2 ) =

∫

1 arctg

cosθ1 sinθ1 sinα1 +εsinθ1 tgα1 tgα2 −εcosθ1 tgα2 +

−π 2 −εm

cosα

dεdθ1

≈ 0;

ε2

−ε2

π 2

εm

ε2 cosθ

sinθ

cosα +εcosθ

tgα

+εsinθ

tgα

D(1) (α ,α ) =

∫

arctg

cosθ1 sinθ1 sinα1 +εsinθ1 tgα1 tgα2 −εcosθ1 tgα2 +

−π 2 −εm

cos

dεdθ1.

(7)

ε2

−ε2

Здесь в обозначениях M(1)

и D(1) нижний индекс показывает вокруг какой оси рассматрива-

ется погрешность поворота, а верхний индекс показывает биения какой оси вызвали эту погреш-

ность. Значение εm в расчётах принималось равным 6″. На рис. 5 представлен график среднего

квадратического отклонения (СКО) σ1(1) (α1,α2)= D1(1)(α1,α2).

Следует отметить, что в (7) в большинстве случаев функцию арктангенса можно заменить её аргументом, т.к. такая замена начинает влиять на точность вычислений только при углах α2, близких к 90°. Кроме того, точное выражение для погрешности, которое следует из (6) — ∆α1 = arctg(tg∆α1)+ πk, где k — целое число и при наблюдении вблизи этой области 90° (направления оси А1) погрешность может быть равной ∆α1 = arctg(tg∆α1)+ π, когда координаты Y′

известия высших учебных заведений. геодезия и аэрофотосъемка, № 6, 2010

p(ε)			σ1(1),"	30
2×105				30
2×105
				20
5×105				10	α2,º	50
				-50	0
			-100
1×105				-50
				-50
5×104			α1,º 0
				50
0
–2×10–5	0	2×10–5 ε, радиан		100
Рис. 4. Арксинусоидальный закон распределения				Рис. 5. График СКО σ1(1)(α1, α2)
	биения оси ОПУ

и X′ одновременно меняют знаки (рис. 6). Причём добавление π влияет только на математическое ожидание, дисперсия остаётся неизменной.

Теперь запишем выражения для погрешности Δα2 поворота вокруг оси А2, вызванной угловыми биениями оси А1, используя (4), (5):

(1)

(α ,α

)= π/2 εm

1 (εcosθ

cosα −εsinθ sinα

)

dεdθ = 0;

∫

π εm2

−ε2

−π 2 −εm

D2(1) (α1) =

π/2

εm

(εcosθ1 cosα1 −εsinθ1 sinα1 )2

dεdθ1.

(8)

∫

π ε2m −ε2

−π 2 −εm

Интеграл (8) можно вычислить аналитически — после преобразований получаем, что это

постоянная величина, равная D2(1) =	ε2
постоянная величина, равная D2(1) =	m .
	4

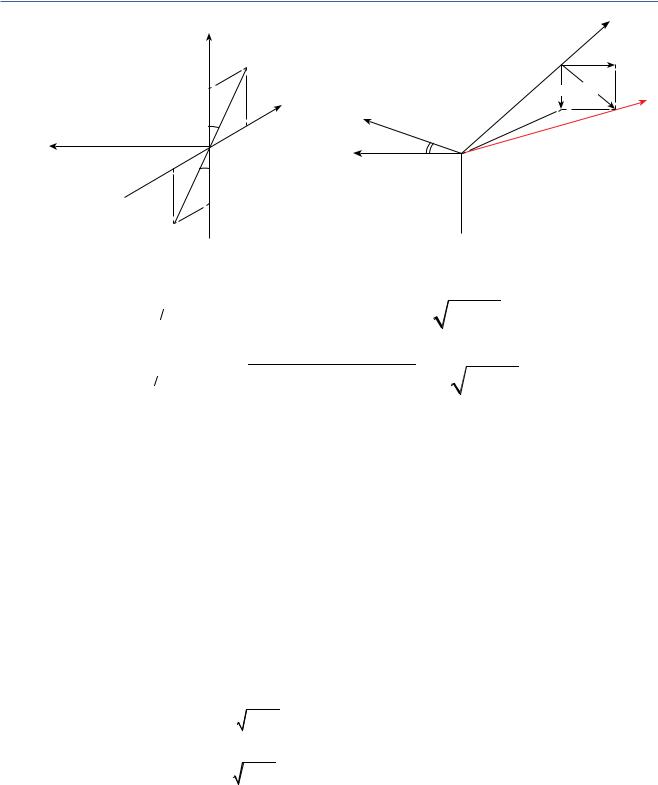
Биения оси А2. Далее рассмотрим биения оси А2 (рис. 7). Аналогично предыдущему случаю, за-
пишем координаты направления смещённой оптической оси в ИСКМ через матрицы поворотов:
		X ′							0
			Y′	= TZ * (α2)TY ′′(ε4)TX ′(α1 +ε3) −1						1	.	(9)

										0
			Z′							0
Из уравнения (9) после преобразований получаем:
					tg∆α1 =			ε3 +ε4 tgα2				(10)
					tg∆α1 =			1−ε3ε4 tgα2				(10)
								1−ε3ε4 tgα2
и Δα	= 0. Далее, т.к. ε3	= εA cosθ2		, ε4	= εA		sinθ2, из (10) следует:
2		2				2
			tg∆α =			εA	cosθ2 +εA sinθ2 tgα2		,			(11)
						2		2
						1−ε2A		cosθ2 sinθ2 tgα2
				1		1−ε2A		cosθ2 sinθ2 tgα2
							2

где εA2 — амплитуда биения оси А2; θ2 — угол биения оси А2 относительно плоскости, проходящей через идеальные исходные (нулевые) положения А2 и оптической оси.

Из (11) получаем следующие выражения для математического ожидания и дисперсии Δα1:

геодезическое приборостроение

Y'	Z'

θ2ε3

ε4 εA2 Z*

Δα		Z'		Y"
Δα	1	Z'
X'(A1)				ε3
				ε3	O
			Y'		O
			Y'

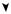X'(A1)

Рис. 6. ПогрешностьΔα1 иΔα1+π

(2)

π/2

εm

εA2

cosθ2 +εA2

sinθ2 tgα2

(α2)=

∫

arctg

1−ε

cosθ

sinθ

tgα

−π 2 −ε

(2)

(α2)=

π/2

εm

εA2

cosθ2 +εA2

sinθ2 tgα2

∫

arctg

1−ε

cosθ

sinθ

tgα

−π 2 −ε

Рис. 7. Биения оси А2

	1
	1				dεA dθ2 = 0;

	2		2
	2		2			2
π		εm −εA2				2
π		εm −εA2
2	1
							dεA dθ2.

	2			2
	2		−	2		2
	π εm			εA		2
	π εm			εA
				2

Неперпендикулярность осей А1 и А2. Влияние неперпендикулярности (рис. 8) на направление оптической оси аналитически выражается в виде такого уравнения:

XYZ

′		0
′	= TZ * (α2)TY" (i)TX ′(α1) −1		1	,	(12)

			0
′			0

где Y″, Z″ — оси, полученные поворотом соответственно Y′, Z′ на угол α1; Z*— получена поворотом Z″ вокруг Y″ на угол i вследствие неперпендикулярности осей.

Из (12) после преобразований выводим известные формулы [2]:

tg∆α1 = i tgα2, ∆α2 = 0.

(13)

Формулу (13) также можно получить как частный случай (10) при ε3= 0, т.е. неперпендикулярность оказывает такое же действие как биение в плоскости осей А1 и А2.

Примем распределение вероятностей неперпендикулярности нормальным. Тогда математическое ожидание и дисперсия погрешности Δα1 вследствие неперпендикулярности следующие:

M1(i

D1(i)

	1	∞	2

) (α2)=		∫ arctg(itgα2 )exp	−i	di = 0;
			2D
	2πD
	i −∞		i

(α	)=	1	∞	arctg(itgα	) 2 exp	−i2	di.
			∫			2D
2		2πD		(	2 )
		i −∞				i

При углах, не приближающихся к области 90°, дисперсию этой погрешности можно считать по формуле

D1(i) (α2)=(tgα2 )2 Di .

(14)

Так, в расчётах максимальная неперпендикулярность принималась равной 15″. Известно, что тангенс угла π/6 отличается от значения дуги угла в радианах на 9,3%. Тогда если приравнять

известия высших учебных заведений. геодезия и аэрофотосъемка, № 6, 2010

Y"	Z*	Y2		Y*
Y"		Y2		Y*
	Z"
	Z"
	-i
	O
		c
		X2
	-i
				Z2(A2)
			c	Z*
X'(A1)	X*	O		Z*


Рис. 8. Неперпендикулярность осей монтировки		Рис. 9. Коллимационная погрешность

(15′′ 5 10−6 )tgα2 = π 6, то α2= 89,992°, т.е. в пределах до 89,992° можно считать, что формулы Δα1= i tg α2 и (14) верны с погрешностью около 9,3%.

Коллимационная погрешность. Влияние коллимационной погрешности (неперпендикулярности оптической оси и оси А2) на итоговую погрешность измерения выражается следующим образом (рис. 9):

X ′								0
Y′		= TX	(c)TZ (α2)TX ′(α1) −1						1	.	(15)
			2	2
									0
	Z′								0
Из (15) после преобразований получаем известные формулы [2]:
		tg∆α =		c	, ∆α		= 0.				(16)
		tg∆α =		cosα2	, ∆α		= 0.				(16)
			1	cosα2		2

Принимая распределение вероятностей коллимационной погрешности также нормальным, запишем формулы для математического ожидания и дисперсии погрешности Δα1:

(c)

(α2)=

∞

−c2

∫ arctg

exp

dc = 0;

cosα

2πD

c −∞

D(c) (α

∞

−c

∫

arctg

exp

dc.

cosα

2πD

−∞

При углах, не приближающихся к области 90°, дисперсию этой погрешности допускается

считать по формуле				2
D(c) (α	)=		1	2	D .	(17)
D(c) (α	)=				D .	(17)
1 2					c
		cosα2

Так же, как в предыдущем пункте, можно оценить, что формулы ∆α =		c	и (17) верны

до 89,97° с погрешностью около 9,3%.	1	cosα2

На основании ОПУ устанавливается трёхосный лазерный гироскоп, который определяет ориентацию основания в местной топоцентрической системе координат. Далее оценим влияние погрешностей гироскопа на измерения.

Погрешность определения курса (рыскания). Пусть X1Y1Z1 (координаты вектора в этой си-

стеме координат будем обозначать А1) — идеальное положение ВСК, параллельной системе координат основания. Через А1 можно выразить координаты вектора А′ в идеальной ИСКМ (X′Y′Z′) (см. рис.2):

геодезическое приборостроение

A′ =TZ (−30°)A1.	(18)
1
Теперь введём погрешность определения рыскания гироскопом Δφp:
Aнепр =TZ * (−30°)TY1 (∆ϕр)A1,	(19)

где Z* — положение оси Z1 после предшествующего поворота на Δφp.

Далее, аналогично предыдущим рассмотренным пунктам, задавая Aнепр единичным вектором, выражая A1 из (18) и подставляя в (19), имеем:

0 A′ =TZ1 (−30°) TZ * (−30°)TY1 (∆ϕр) −1 1 .

После преобразований из этого уравнения получаем следующие значения погрешностей углов поворотов осей А1 и А2 ОПУ, вызванных погрешностями определения рыскания гироскопом:

	2sin∆ϕ		∆ϕ				3	1−cos∆ϕ
∆α =	р	≈	р	; ∆α		=	(		р )≈ 0.	(20)
∆α =	cos∆ϕ +3	≈	2	; ∆α		=	4		р )≈ 0.	(20)
1	cos∆ϕ +3		2		2		4
	р

Погрешность определения дифферента (килевой качки). Аналогично предыдущему пун-

кту, получаем следующее уравнение для координат вектора, задающего оптическую ось, с учётом погрешности дифферента:

																	0
	A′ =TZ (−30°) TZ							(−30°)TZ				(∆ψ) −1						1	.
	1				1						1
																		0
Откуда следует, что																		0
Откуда следует, что
			∆α1 = 0 и ∆α2 = ∆ψ.																			(21)
Погрешность определения крена (бортовой качки).
Для координат вектора с учётом погрешности бортовой качки имеем:
																	0
	A′ =T (−30°)				T *			(−30°)T				(∆θ			к	) −1		1	.			(22)
			Z1		Z					X1					к
																		0
																		0
Из (22) получаем следующие выражения:
	2						∆θк
∆α =	2	3sin∆θк		≈		3	∆θк		; ∆α		=			3		(cos∆θ					−1) ≈ 0.	(23)
∆α =				≈					; ∆α		=		4			(cos∆θ					−1) ≈ 0.	(23)
1	3cos∆θк +1				2					2			4							к

Если для других корабельных комплексов требуется передавать координаты в КСК, то по-

грешность положения ВСК относительно КСК можно записать так:
Δφ = Δφp1 – Δφp2,	(24)

где Δφ — погрешность взаимного положения КСК и ВСК в плоскости рыскания; Δφp1 — погрешность рыскания в КСК; Δφp2 — погрешность рыскания в ВСК.

Тогда дисперсия погрешности Δφ равна:

D∆ϕ = D∆ϕ1 + D∆ϕ2 .

(25)

Аналогичные (24) и (25) равенства можно записать и для погрешностей в плоскостях дифферента и крена.

известия высших учебных заведений. геодезия и аэрофотосъемка, № 6, 2010

Тогда из (20), (21), (23) можно выразить дисперсии погрешностей Δα1 и Δα2, вызванные погрешностями взаимного положения КСК и ВСК:

+ D

+ D ; D

= D

+ D .

∆α1

( ∆ϕ1

∆ϕ2

)

( ∆θ1

∆θ2 )

∆α2

∆ψ1

∆ψ2

Погрешности положения центра пересечения осей А1

и А2. Вводя вектор погрешностей

∆x

, получим

Aнепр

=TZ (−30°)[A1 − A∆ ]= A′−TZ (−30°)A∆, откуда следует:

A∆ =

∆y

∆z

A′ = Aнепр +TZ (−30°)A∆ .

(26)

зададим равным

3 105

, т.к. в данном случае играет роль расстояние до цели, типич-

непр

ное значение которого равно 300 км.

Из уравнения (26) выражаем углы поворота осей монтировки:

tg∆α =

∆z

, sin∆α

∆y −

∆x

∆

6 105

+3 105

x, z и видно, что только смещение по оси OZ на

На рис. 10 показана зависимость Δα1

от

2 м вызывает погрешность около 1″. Из рис. 11 видно, что смещение по оси OX и OY на 1 и –1 м соответственно вызывает погрешность Δα2 около 1″. Таким образом, в рассматриваемой задаче линейные смещения слабо влияют на результирующие погрешности угловых измерений.

Суммарные погрешности. Учитывая (4), (6), (11), (13), (16), (20), (21), (23), для систематиче-

ских погрешностей имеем следующие формулы:

ε2A cosθ1 sinθ1 cosα1

+εA cosθ1 tgα1 tgα2 +εA sinθ1 tgα2

∆α1 = arctg

ε2

cos

θ sinθ sinα +ε

sinθ

tgα

−ε

cosθ

tgα

cos

εA

cos

θ2

+εA

sinθ2 tgα2

∆ϕp

∆θ

+arctg

+arctg(i tgα2 )+arctg

;

cosθ2 sinθ2 tgα2

1−εA

cosα2

∆α2 = (ε1 cosα1 −ε2 sinα1 )+ ∆ψ.

Как уже оговаривалось — для всех углов поворота, кроме области, близкой к α2= 90°, можно заменить функции арктангенса их аргументами. Далее перейдём к характеристикам случайных

погрешностей:

)+ 1 D

+ 3 D

= 0;

(α ,α

) = D(1)

(α

,α

)+ D(2)

(α

)+ D(i) (α

)+ D(c) (α

+ D ,

1 2

4 ϕр

4 θк

скр

где M1 — математическое ожидание погрешности Δα1; D1(α1, α2) — дисперсия погрешности Δα1;

Dϕp — дисперсия погрешности измерения рыскания;

Dθ

— дисперсия погрешности измерения

бортовой качки; Dскр

— дисперсия скручивания каждой из осей А1 и А2.

= 0; D =

ε2

m + D + D ,

скр

где M2 — математическое ожидание погрешности Δα2; D2 — дисперсия погрешности Δα2; Dψ — дисперсия погрешности измерения дифферента.

геодезическое приборостроение

α1

α2

0,5″

								-0,5"
								-0,5"							1
-1"													0,5
													0,5
												0
												0				y,м
-2					1	2		-1		-0,5
										-0,5
				0

		-1
		-1
-1							z,м	-1
-1							z,м	-1
-0,5								-0,5
-0,5								-0,5
0								0
0,5								0,5
									1

1			х,м								х,м


	Рис. 10. ЗависимостьΔα1 от					x и z		Рис. 11. ЗависимостьΔα2 от x и						y

Так как погрешности углов Δα1 и Δα2 складываются из достаточно большого числа статистически независимых погрешностей, то результирующие законы распределения вероятностей принимаем за нормальные.

Далее от математических ожиданий и дисперсий углов поворота Δα1 и Δα2 осуществлялся переход к статистическим характеристикам непосредственно одной угловой погрешности измерения. Угловая погрешность измерения может быть вычислена через скалярное произведение двух единичных векторов — идеального направления оптической оси и вектора, смещённого за счёт рассматриваемых погрешностей.

Координаты единичного вектора в ИСКМ можно выразить через углы поворота ОПУ следующим образом:

	X ′	−sinα2
				(27)
Y′		= cosα1 cosα2	.	(27)

	Z′	sinα1 cosα2

Тогда, учитывая (27), можно получить следующее выражение:

sin2 ∆ϕ =1− sinα2 sin(α2 + k∆α2 )+cosα1 cosα2 cos(α1 + k∆α1 )cos(α2 + k∆α2 )+

1	2	sin	( 1	1 )	cos	( 2	+ k∆α	2 )	2 ,	(28)
+sinα cosα			α + k∆α			α

где Δφ — угловая погрешность измерения; k — коэффициент перехода от угловых секунд к радианам, равный π/180·3600.

Математическое ожидание MΔφ=0. Принимая условие, что ввиду малости погрешностей
sinΔφ ≈ Δφ, дисперсия угловой погрешности измерения вычисляется по формуле:
									1				1			∞ ∞								2				exp					2	d∆α d∆α
D (α ,α			) =						1				1			∫ ∫ sin2 ∆ϕexp							−∆α1								−∆α2						. (29)
		2																													−∆α2
																											2						2
∆ϕ	1						2πD1(α1,α2 ) 2πD2 −∞ −∞																				2						2		1	2
							2πD1(α1,α2 ) 2πD2 −∞ −∞													2D1(α1,α2 )											2D2
После преобразований (28), подстановки в (29) и взятия интегралов получим:
D	(α ,α			2	) = − cos4 α2							3e−2k2D2			+e−2k2			(D1+D2 )	−4e−k2(D1				2+2D2 )		+
∆ϕ	1			2					2
									2
						+		1	cos	2	α2	(−e	−2k2D				−2k	2D	−2k2(D +D		)	−8e		−k2(D		2+2D			)	+1)	+	1	(1	−e	−2k2D	),	(30)
						+		4	cos		α2	(−e		1 +7e				2 +e	1	2		−8e			1			2		+1)	+	2	(1	−e	2	),	(30)
								4																								2

известия высших учебных заведений. геодезия и аэрофотосъемка, № 6, 2010

где D1 = D1(α1, α2).
Далее к дисперсии (30) необходимо прибавить некоторые другие составляющие:
D∆ϕ∑ (α1,α2 ) = D∆ϕ (α1,α2 )+ Dдеф + Dооскр + Dнагр + Dтеплвмд ,		(31)
где DΔφΣ(α1, α2) — дисперсия суммарной угловой погрешности; Dдеф	— дисперсия отклонения
оптических осей за счёт деформации ОПУ и опорного блока; Dооскр	— дисперсия отклонения
оптических осей за счёт скручивания осей ОПУ, вызываемого неуравновешенностью вращаю-

щихся частей, сопротивлением от скручивания кабелей и моментами сопротивления в опорах
качения; Dнагр — дисперсия отклонения оптических осей за счёт деформации ОПУ от нагрева
при прямом солнечном облучении; DтеплВМД							— дисперсия отклонения оптических осей за счёт
деформации ОПУ от тепловыделений высокомоментных двигателей.
σϕ	СКО	частных		погрешностей		были заданы следующими: σi = 5″; σc = 20,6″; σскр = 1″;
	=σθ = σ		= 3,(3)″; σ		= 2,7″; σ	= 0,7″; σ	нагр	= 5,7″; σ	теплВМД	= 1,7″. На рис. 12 представлен гра-
p	к	ψ		деф	ооскр

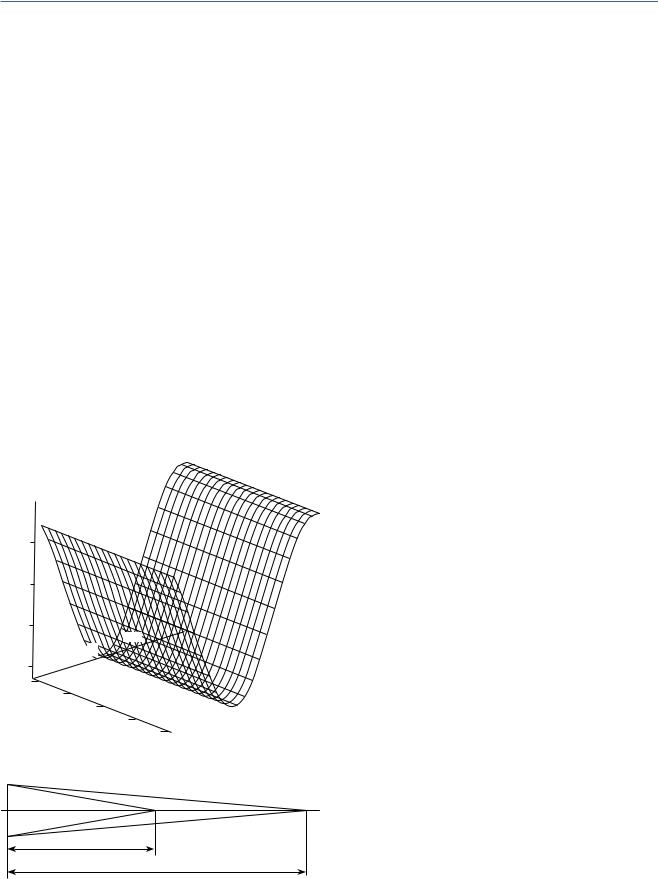
фик СКО суммарной угловой погрешности. Оценим значение погрешности в КСК (Δφ′) в зави-

симости от подсчитанной выше суммарной угловой погрешности в ИСКМ (ΔφΣ). Наибольшее различие углов ΔφΣ и Δφ′ (рис. 13) будет при наибольшей разнице расстояний от объекта до этих двух систем координат ИСКМ и КСК — 63,6 м (расстояние между точками Ц0 и Ц1), т.е. когда объект расположен на продолжении линии, соединяющей Ц0 и Ц1 (см. рис.2). При этом

∆ϕ′	=	3 105	= 0,9998,
		3 105 +63,6
∆ϕΣ

т.е. суммарную угловую погрешность в КСК можно считать равной погрешности в ИСКМ с дисперсией (31).

σΔφ∑

21,6"

21,5"

21,4"

α2 0 50º 21,3" -50º

-100

-50º

100º α1

Рис. 12. СКО суммарной угловой погрешности

		Ц1		Ц0
Δφ	Σ	Ц1	Δφ'	Ц0
Δφ	Σ		Δφ'

3·105

3·105+63,6

Таким образом, предложена методика определения угловой погрешности вследствие биений в произвольной плоскости, других геометрических погрешностей, а также погрешностей определения качек, с учётом применения в комплексе нестандартной монтировки. Были получены выражения вероятностных характеристик угловой погрешности измерения комплекса в зависимости от вероятностных характеристик частных погрешностей и углов поворота для всего диапазона их изменения.

ЛИТЕРАТУРА

1.Авзалов И.З. Методика пересчёта координат корабельного оптического комплекса // Изв. вузов. «Геодезия и аэрофото-

съёмка». 2010. –№ 2. –С. 95–98.

2.Высокоточные угловые измерения / Д.А. Аникст,

К.М. Константинович, И.В. Меськин и др.; Под ред. Ю.Г. Якушенкова. –М.: Машиностроение, 1987. –480 с.

3. Дворяшин Б.В. Метрология и радиоизмерения: Учеб. пособие для студ. высш. учеб. заведений. –М.: Академия, 2005. –304 с.

Поступила 23 сентября 2010 г. Рекомендована кафедрой прикладной оптики МИИГАиК

Рис. 13. Угловые погрешности в ИСКМ и КСК

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.2015254.96 Кб23земелька курсач.rtf
#
17.09.201950.63 Кб3Земельное право.docx
#
17.09.201982.85 Кб3Земельное право.docx
#
02.05.2015117.76 Кб14Земельный Фонд.doc
#
26.04.2019407.87 Кб19Из ПДФ.docx
#
02.05.20153.51 Mб52Известия вузов Геодезия и аэрофтосъемка №6.pdf
#
02.05.2015223.74 Кб34Измерение цифровых снимков.doc
#
29.08.2019151.04 Кб2Илюшина .doc
#
24.11.20191.33 Mб6Инженерное обустройство территорий.docx
#
02.05.2015631.81 Кб12инструкция по атс полигонометрия.pdf
#
10.03.2016577.02 Кб69ИНСТРУКция по ФГМ работам.DOC