
мат.ан. заоч / Дифференц. исчисление
.pdfМатематический анализ Дифференциальное исчисление
Доцент Матвеева А.С. anmatveeva@yandex.ru
2. Производная функции
Определение. Производной функции у =f(x) в точке х называется конечный предел отношения приращения функции в этой точке к приращению аргумента,
при условии, что приращение аргумента стремится к нулю.
|
f (x x) f (x) |
|
f (x) lim |
|
|
x |
||
x 0 |
Замечание Производная функции в точке - это число. Если рассматривать множество чисел,
на котором производная существует, то получают производную, как новую функцию.
Производную обозначают: уי(х); fי(x); уי. Операция нахождения производной называется
дифференцированием. Если функция имеет производную, то ее называют гладкой.
3. Простейшие правила дифференцирования
Обозначим u= f(x) , v = g(x) - функции, дифференцируемые в точке х, с- постоянная.
1) Производная суммы или разности функций равна сумме или разности их
производных: |
(u v) = u v |
2)Постоянный множитель с выносят за знак производной: (с v) = сv
3)Производная произведения: (u v) = u v + u v
4) Производная частного: |
|
|
|
|
|
|
u |
|
|
u v v u |
|||
|
|
|
|
|
|
|
|
|
|
v2 |
|||
v |
|
|
|
|||
Производной второго порядка функции у =f(х) называется производная от ее производной. Обозначают у׳׳

4. Производные некоторых функций
С = 0
постоянная
(xm) = mx. m-1
|
|
степенная |
|
|
|
|
|
||||||
(x) = 1 (m=1) |
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
(x2) = 2x (m=2) |
2 x |
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|||
3 |
|
2 |
|
|
|
|
1 |
|
|
||||
(x ) |
= 3x |
|
|
|
|
|
|
|
|
||||
|
|
x2 |
|
||||||||||
(m=3) |
|
|
x |
|
|
|
|
|
|||||
(ax+b) = a
линейная
ex ex
ln x 1x
(m=?) для средних формул
5. Производная сложной функции
• . |
|
|
|
|
|
Пусть y = f(u); u = g(x), тогда y |
|||||
|
f (u) u |
|
Пример: Найти производную функции y=ln(2x-3).
Здесь y=lnu, u=2x-3, тогда уי=(1/u)·uי = (1/(2x-3))(2x-3)י
y |
1 |
|
2 |
0 |
|
|
|||
(2x 3) |
||||
|
- |
|
|
|
Пример (для самостоятельного решения ): y= e-3х
Найти производную функции в нуле.
6. Нахождение производных
• |
Примеры. Найти производные уי и уיי. |
• |
1) у=5 уי =0 уיי =0 2) у =3-2х уי =-2 уיי =0 |
• 3) у=3х2-4х+7 уי =6х-4 уיי =6
• 4) у=-4х3+3х2-4х+7 уי =-12х2+6 х-4 уיי =-24х+6
• |
5) у =ln(3-2х); уי = 1/(3-2x)·(-2)=(-2)/(3-2x); уיי=(-4)/(3-2x)2 |
• |
6) у = e-3x ; уי = e-3x(-3x)י=(-3)· e-3x; уיי=9 e-3x |
•Найдем уי(0). Уי(0)=(-3) · e-3·0= (-3)· e·0=-3·1=-3
•Ответ: -3

7. |
Пример 2. Найти производную функции |
|
. |
3x 1 y= 2x 1
|
3x 1 |
|
|
|
5 |
||
|
(3x 1) (2x 1) |
(3x 1)(2x 1) |
|
||||
y ( |
|
) |
|
|
|
|
|
2x 1 |
(2x 1)2 |
(2x 1)2 |
|||||
8. Исследование функций с помощью производных
Возрастание и убывание дифференцируемых функций.
Теоремы. Необходимое и достаточное условия возрастания функции. 1)Если функция f(x) возрастает на отрезке [a, b], то f (x) 0. на этом отрезке. 2) Если f (x)>0 , то f(x) возрастает на отрезке [a, b].
Теоремы. Необходимое и достаточное условия убывания функции.
1) Если функция f(x) убывает на отрезке [a, b], то f (x) 0 на этом отрезке. 2) Если f (x)<0 , то f(x) убывает на отрезке [a, b].
Возрастающие и убывающие функции называются монотонными.

9. Исследование на монотонность функции
• Исследовать на монотонность функцию
у 3x 1 2x 1
|
3x 1 |
|
. |
|
|
5 |
|
||
|
(3x 1) (2x 1) |
(3x 1)(2x 1) |
|
|
|||||
y ( |
|
) |
|
|
|
|
|
0 |
|
2x 1 |
|
(2x 1)2 |
(2x 1)2 |
||||||
• функция возрастает на всей области определения
10. Экстремумы функции
•Определение. Точки максимума и минимума называются
точками экстремума, а значения функции- экстремумами.
Теорема. (необходимое условие существования гладкого экстремума)
Если функция f(x) дифференцируема в точке х = х0 и точка х0 является точкой экстремума, то производная функции обращается в нуль в этой точке. Определение. Стационарными точками функции называются точки, в которых производная функции равна нулю. Гладкий экстремум может находиться только в стационарных точках функции.
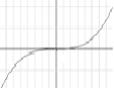
Замечание. Не всякая стационарная точка является точкой экстремума, например, у функции у=х3 точка х=0 будучи стационарной точкой, не является
точкой экстремума.( см. рис.) |
у=х3 |
||
|
|
|
|
|
|
х=0 |
|
|
|
|
|
