1. Восстановление весов частных критериев оптимальности по принятым решениям

В общем случае задача может быть представлена следующим образом:

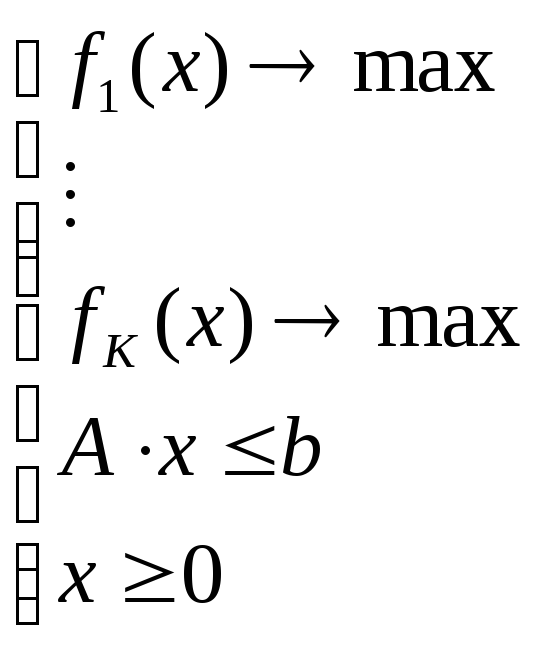, где f_k – частные критерии оптимальности, х – вектор-столбец инструментальных переменных, А – технологическая матрица, b – вектор-столбец ограничений ресурсов.

Если считать, что f_k – линейна, т.е. f_k (х) = (с^к)^Тх, то исходная задача может быть представлена в следующем виде:

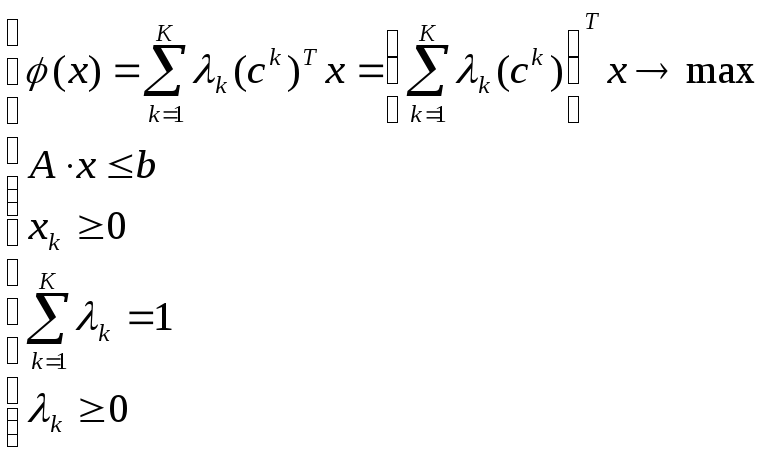, где _к – искомые веса частных критериев с^к.

По условию Куна-Такера необходимые и достаточные условия достижения максимума функции в точке х^opt имеют вид:

, где - градиент целевой функции по направлению и , - i – тая нормаль для ограничений A*x  b и , у_i – i-тая двойственная оценка, v_j – неотрицательное число, е – единичная компонента.

Таким образом, получаем следующую систему соотношений:

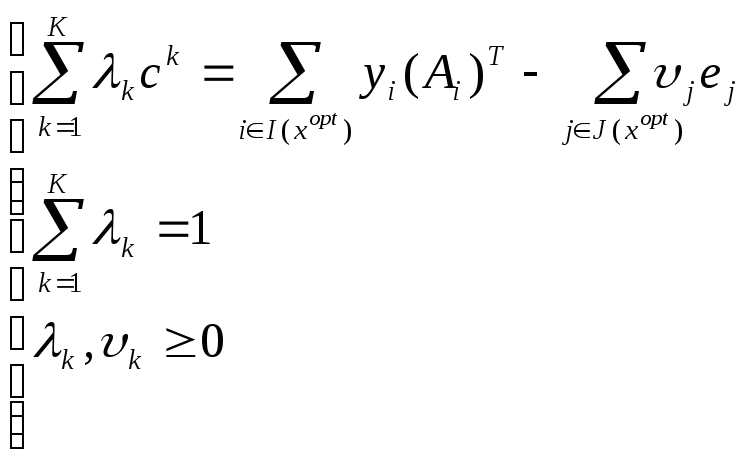
В результате могут быть получены следующие ситуации:

1. Решение единственно.

2. Множество решений.

3. Пустое множество.

II. Восстановление весов частных критериев по одному наблюдению

Приложение 1.

Исходные данные. 3-й период.

Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений : I={1,2,3}

Множество активных ограничений : J={2,5}

В данном случае система уравнений записывается следующим образом:

Так как у_i могут быть любого знака, то введем у_i = у_i⁺ - у_i^-. Запишем полученную систему в явном виде.

Для этого определили множество I(x^opt), куда войдут ограничения типа А*х^opt=b. Сама система будет записана следующим образом:

60

*

1

+

30

*

2

-7

*

у1

-6

*

у2

-13

*

у3

+

q1

=

0

11

*

1

+

69

*

2

-5

*

у1

-6

*

у2

-20

*

у3

+

2

+

q2

=

0

25

*

1

+

50

*

2

-10

*

у1

0

*

у2

-17,5

*

у3

+

q3

=

0

10

*

1

+

20

*

2

0

*

у1

-5

*

у2

0

*

у3

+

+

q4

=

0

10

*

1

+

28,8

*

2

-2

*

у1

-1

*

у2

-13,8

*

у3

5

+

q5

=

0

₁ + ₂ = 1

_к  0, к=1,2

y_i^s  0, iI

_j  0, jJ

Следует учесть, что в результате решения может быть получено множество решений для _к. Условием не единственности полученного решения является наличие небазисной переменной, для которой оценочный коэффициент равен нулю, т.е. внесение этой переменной в базис не повлияет на значение целевой функции. В рассматриваемой системе предлагается использовать следующую логику рассуждений для определения иных базисных решений:

появление в решении небазисных переменных с равными нулю оценочными коэффициентами свидетельствует, как уже было описано выше, о наличии других решений системы;

признаками принадлежности исходного решения базисному (опорному плану) являются _j , причем _j = 0 – переменная базисная, _j > 0 – переменная не базисная;

на основе выше сказанного, переход от одного базисного решения к другому предлагается осуществлять простым исключением (приравниванием нулю) какого-либо значения _j из предлагаемой и системы, тем самым, включая соответствующий x_j в базис;

критерием включения того или иного х_j в базис будет отсутствие в базисе искусственно введенных переменных q_i , так как по условию они должны быть исключены из опорного плана (_j в этом случае должно на себя оттягивать любое значение с q_i), и, следовательно, включать соответствующую j - тую технологию в первоначальный оптимальный план нельзя.

Таким образом, в результате проведенного анализа может быть получено множество  такое, что , 0    1.

Используя предложенный способ анализа в пакете линейного программиования BLP 88, были получены следующие результаты:

1. ₁¹ = 0., ₂¹ = 0., при ₁ = 12.14, ₄ = 6.43 и невошедших в базисное решение y11 и у12, т.е. опорный план (х₂,х₃,х₅) ;

2. ₁² = 0.4988, ₂² = 0.5012, при ₂ = 6,882 и не вошедшим в базисное решение ₅.

Тогда искомое решение будет представлено следующим образом: