Московский Государственный Институт Электронной Техники

(Технический Университет)

кафедра Высшей математики

КУРСОВАЯ РАБОТА

по

“Методам прикладной математики”

на тему

“Приближённое решение краевых задач математической физики методом сеток.”

Выполнила: Морозова А.В. Руководитель: Соколова Т.В.

Москва, 1999 год.

Линейные уравнения второго порядка в частных производных.

Классификация задач. Линейное уравнение второго порядка в частных производных в общем случае имеет вид:

(1)

где a, b, c, d, e, g, f - известные функции от x и y. Если a, b, c, d, e, g – константы, то (1) называется уравнением с постоянными коэффициентами. Если f(x, y)=0, то уравнение является однородным.

Уравнение (1) называется эллиптическим, если D < 0; гиперболическим,

если D > 0; параболическим, если D = 0. D - дискриминант квадратичной формы :

При помощи невырожденного преобразования U(x, y)

уравнение (1) можно привести к одному из следующих канонических видов:

эллиптический

гиперболический

параболический

Постановка задач. При математическом описании физического процесса надо прежде всего поставить задачу, т. е. сформулировать условия, достаточные для однозначного определения процесса. Дифференциальные уравнения имеют бесчисленное множество решений, поэтому для однозначного определения процесса необходимы также дополнительные условия  краевые и начальные. Краевые и начальные условия зависят от типа уравнения. Задача, в которой поставлены краевые и начальные условия называется смешанной задачей.

Первая краевая задача для уравнения колебаний струны.

Рассмотрим струну длиной l, закрепленную в точках x=0, x=l. Положение каждой точки струны характеризуется значением координаты x. Пусть U=U(x, t)  вертикальное отклонение струны в точке x в момент времени t от положения равновесия.

Так как концы струны закреплены, то в любой момент времени должны выполняться граничные условия U(0,t) = 0; U(l,t) = 0. Процесс колебания струны зависит от ее начальной формы и от распределения скоростей, поэтому задаются начальные условия:

Начальные и граничные условия определяют решение уравнения струны.

где

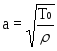
- натяжение струны;

p - плотность материла струны;

f(x,t) - плотность внешней силы, рассчитанная на единицу длины струны.

Если концы струны движутся по заданному закону, то граничные условия принимают другой вид: U(0,t) =(t); U(l,t) =(t). Возможны также и другие типы граничных условий.

Итак, первая краевая задача для уравнения колебаний струны ставится следующим образом:

Найти функцию U(x,t), определенную в области ,, удовлетворяющую

уравнению:

0 < x < l, t > 0.

а также следующим граничным условиям:

U(0,t) =(t); U(l,t) =(t) , t > 0

и начальным условиям:

U(x,0) =(x), U_t(x,0) = (x),,

где ,,,,f - заданные функции; a - известная постоянная.

2. Постановка задачи.

U_tt=U_xx:

Начальные условия:

U(x,0)=20sin((3/4)x);

U_t(x,0)=0;

Граничные условия:

U(0,t)=0:

3U(1,t)+4U_x=0;

2 Решение задачи с помощью явной разностной схемы

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам:

2.1 Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем шаблон "крест".

Получаем конечно-разностную систему:

Обозначим =/h и выразим U(i,j+1) через остальные значения сеточной функции, входящие в уравнение:

(1)

Уравнение (1) должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями, получаемыми из аппроксимации краевых и начальных условий.

2.2 Аппроксимация 1-го начального условия.

(2)

2.3 Аппроксимация 1-го граничного условия.

U(0,j)=0, (3)

2.4 Аппроксимация 2-го начального условия.

Для более точного аппроксимирования 2-го начального условия разложим U(x, t) в окрестности точки (x,0) по формуле Тейлора:

Используя 1-ое и 2-ое начальные условия, переходим к конечным разностям:

(4)

Формула (4) используется на начальном этапе для вычисления значения функции U(x, t) на первом слое, по известным значениям функции на нулевом слое и на границе.

2.5 Аппроксимация 2-го граничного условия.

Для более точного аппроксимирования 2-го граничного условия разложим U(x, t) в окрестности точки (1, t) по формуле Тейлора:

Используя уравнение краевой задачи и второе граничное условие, получаем:

Перейдем к конечным разностям, записываемым в узле U(m-1,j), получаем:

(5)

Выражая из него U(m,j+1) получаем:

Найдем точку U(m,1) из (4), при i=m:

(6)

Откуда выразим U(m+1,0):

(7)

Из (5), при j=0:

(8)

Из (1), при i=m, j=0:

Погрешность аппроксимации o(h²+²). Схема устойчива при   h.

Итак, U(i, j) при j=0 и j=1 определены. Включается рекуррентная процедура, описываемая уравнением (1) и вычисляется U(i, j) для всех i=1,2,...,m-1, для каждого фиксированного j=2,...,n-1. Текст программы в среде Matlab приведен в Приложении (стр.12). Поверхность функции являющейся решением нашего дифференциального уравнения изображена в Приложении (стр.14).