Содержание

Постановка задачи 3

Решение задачи с помощью явной разностной схемы 4

1. Аппроксимация дифференциального уравнения 4

2. Аппроксимация 1-го начального условия 4

3. Аппроксимация 1-го граничного условия 4

4. Аппроксимация 2-го начального условия 5

5. Аппроксимация 2-го граничного условия 5

6. Устойчивость решения. 5

Решение задачи с помощью неявной разностной схемы 6

1. Аппроксимация дифференциального уравнения 6

2. Аппроксимация 1-го начального условия 6

3. Аппроксимация 2-го начального условия 6

4. Аппроксимация 2-го граничного условия 6

5. Аппроксимация 1-го граничного условия 6

6. Вычисления прогоночных коэффициентов 7

Приложение 9

Явная схема 9

Результат 10

Неявная схема 11

Результат 12

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ : 13

Постановка задачи

Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической физики методом сеток.

(1)

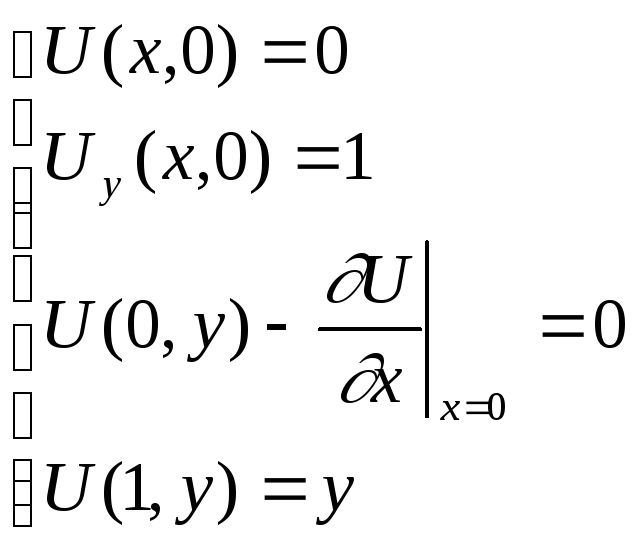0 < x,y < 1 (2).

Данное уравнение является уравнением гиперболического типа и физически отражает процесс колебания струны. Искомое решение U=U(x,y) – вертикальное отклонение струны в точке х в момент времени y.

Данная краевая задача состоит в нахождении функции U=U(x,y), удовлетворяющей уравнению (1), а также заданным начальным и граничным условиям (2).

Граничное условие первого рода U=U(1,y) определяет закон движения правого конца струны. Для левого конца в качестве граничного условия задано так называемое условие «упругого конца» (граничное условие третьего рода):

Ux (0,y)=U(0,y) .

Начальные условия U(x,0)=0 и Uy(x,0)=1 задают начальную форму струны и распределение скоростей в начальный момент времени.

Функция f(x,y) имеет смысл плотности внешней силы, рассчитанной на единицу длины.

Решение задачи с помощью явной разностной схемы

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам:

1. Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем шаблон "крест".

Получаем конечно-разностную систему:

Обозначим g=/h и выразим U(i,j+1) через остальные значения сеточной функции, входящие в уравнение:

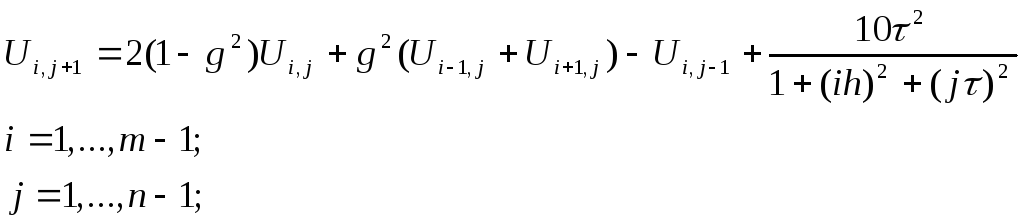(3)

Уравнение (3) должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями, получаемыми из аппроксимации краевых и начальных условий.

2. Аппроксимация 1-го начального условия

(4)

3. Аппроксимация 1-го граничного условия

Аппроксимация краевого условия третьего рода используется только для нахождения решения на границе i=0 в явном виде:

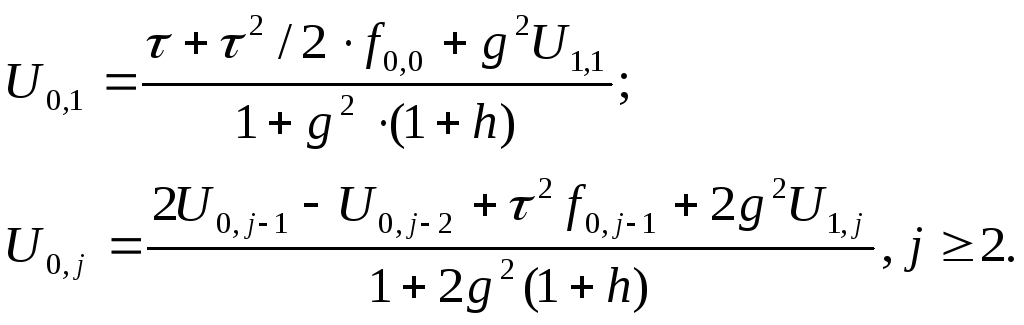(5)

4. Аппроксимация 2-го начального условия

Для более точного аппроксимирования 2-го начального условия разложим U(x,y) в окрестности точки (x,0) по формуле Тейлора и, используя 1-ое и 2-ое начальные условия, перейдем к конечным разностям:

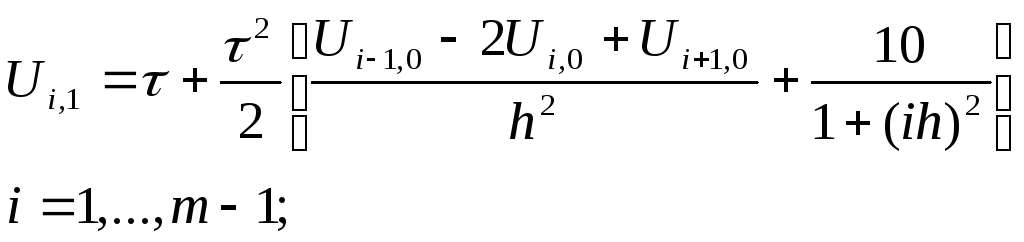(6)

Принимая во внимание уравнение (4) получаем:

(7)

Формула (7) используется на начальном этапе для вычисления значения функции U(x,y) на первом слое, по известным значениям функции на нулевом слое и на границе.

5. Аппроксимация 2-го граничного условия

(8)

Порядок аппроксимации данной разностной схемы

6. Устойчивость решения.

Для уравнений гиперболического типа метод спектральных гармоник приводит к следующему условию устойчивости:

(9)

т.е. если это условие устойчивости не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою.

Отсюда, в частности, получаем для явной схемы () условие устойчивости Куранта-Леви: .

Итак U(i,j ) при j=0 и j=1 определены. Включается рекуррентная процедура описываемая уравнением (3) и вычисляется U(i,j ) для всех i=1,2,...,m-1 , для каждого фиксированного j=2,...,n-1.

Решение задачи с помощью неявной разностной схемы

Рассмотрим снова нашу краевую задачу . Для аппроксимации уравнения используем Т-образный пятиточечный шаблон.

Уравнение аппроксимируется следующими уравнениями :

1. Аппроксимация дифференциального уравнения

(10)

Обозначим g=/h и приведем (10) к виду удобному для применения метода прогонки:

(11)

2. Аппроксимация 1-го начального условия

, (12)

3. Аппроксимация 2-го начального условия

Для более точного аппроксимирования 2-го начального условия разложим u(x,y) в окрестности точки (x,0) по формуле Тейлора и используя 1-ое и 2-ое начальное условия перейдем к конечным разностям:

(13)

Запишем (13) к виду удобному для применения метода прогонки:

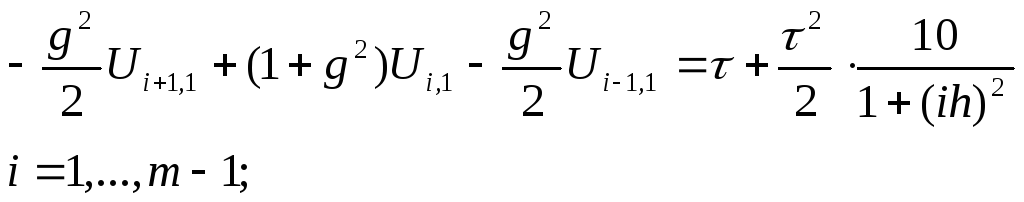
(14)

4. Аппроксимация 2-го граничного условия

(15)

5. Аппроксимация 1-го граничного условия

в узле(0,1):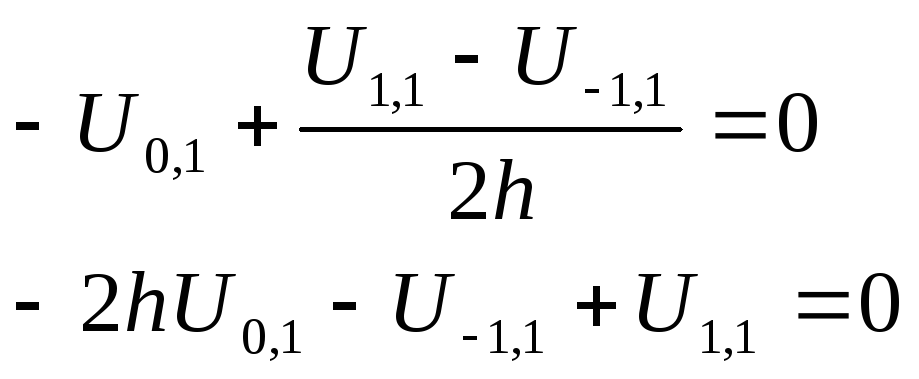

(14) при i=0 будет:

исключая фиктивный узел, получим:

(16)

при j2, в узле (0,j):

(11):, тогда:

(17)

6. Вычисления прогоночных коэффициентов

Сначала найдем u(i,j) на слое j=1. Определим прогоночные коэффициенты.

Обозначим , тогда, используя (16),(14) и (15) получим систему:

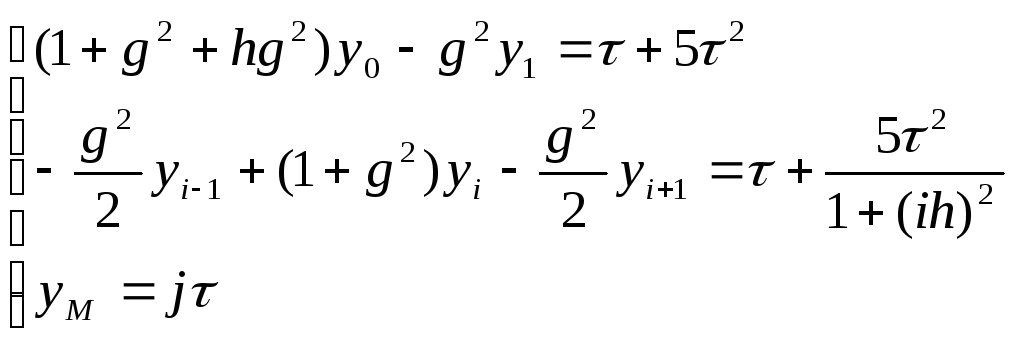
получим прогоночные коэффициенты:

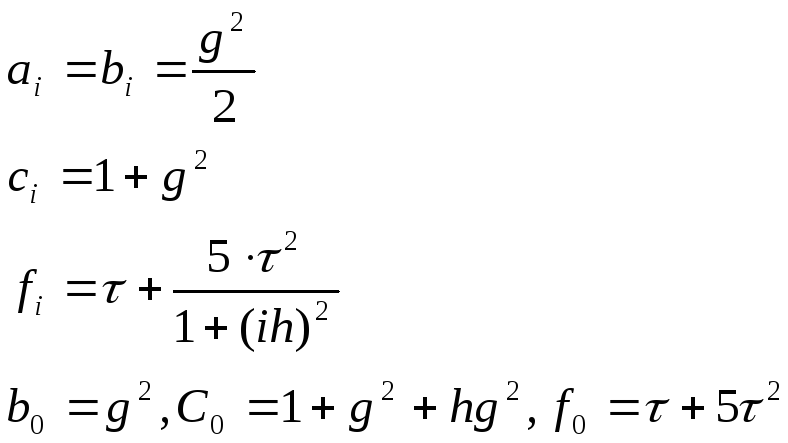
Теперь вычислим граничные прогоночные коэффициенты:

Методом прогонки находим u(i,1), где i=1...m;

Теперь зная значения j=0,1 находим u(i,j ), где j=2...n.

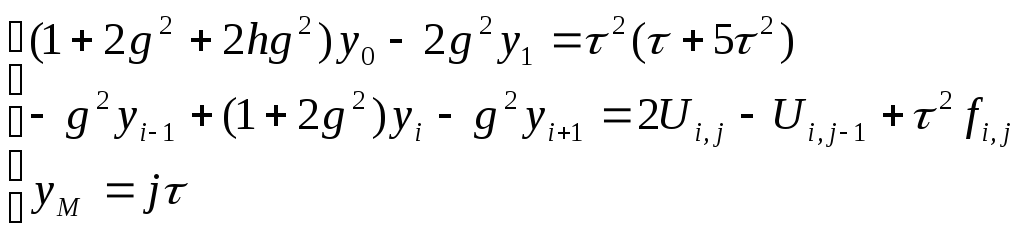
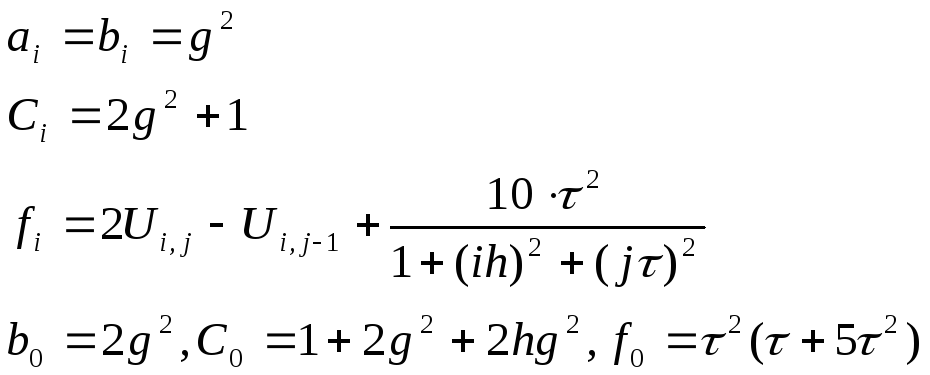
Теперь вычислим граничные прогоночные коэффициенты:

Методом прогонки находим u(i,j), где i=1...m ,j=2..n ;

Приложение

Ниже приведены две программы для численного решения задачи на ПК в среде MATLAB и результаты их выполнения для явной и неявной разностных схем.

Явная схема

function y(M,N);

h=1/M;

t=1/N;

if t>h

for i=1:10,disp(' ');,end;

disp(' ВОЗМОЖНА НЕУСТОЙЧИВОСТЬ!!!');

disp(' (невыполнено условие устойчивости Куранта-Леви:t<=h)!!!');

pause

end;

t2=t^2;

h2=h^2;

g=t2/h2;

U=zeros(M+1,N+1);

S=zeros(M+1);

% (8)

for j=1:N+1

U(M+1,j)=(j-1)*t;

end;

% (7)

for i=2:M

U(i,2)=t+5*t2/(1+((i-1)*h)^2);

S(i)=U(i,2);

end;

% (5.1)

U(1,2)=(t+5*t2+g*U(2,2))/(1+g*(1+h));

% (3)

for i=2:M

U(i,3)=2*(1-g)*U(i,2)+g*(U(i-1,2)+U(i+1,2))-U(i,1)+(10*t2)/(1+(i*h)^2+t2);

end;

for j=3:N

for i=2:M

U(i,j+1)= 2*(1-g)*U(i,j)+ g*(U(i-1,j)+U(i+1,j))-U(i,j-1) + (10*t2)/( 1+ ((i-1)*h)^2 + ((j-1)*t)^2 );

end;

% (5.2)

U(1,j)=( 2*U(1,j-1) - U(1,j-2) + t2 * (10/(1+(t*(j-2))^2)) +2*g*U(2,j) ) /(1+2*g*(1+h));

end;

j=N+1;

U(1,j)=( 2*U(1,j-1) - U(1,j-2) + t2 * (10/(1+(t*(j-2))^2)) +2*g*U(2,j) ) /(1+2*g*(1+h));

contour(U,20);pause;

for j=0:N,

i=1:1:M;

u1=U(i,j+1);

plot(i,u1);

end;

mesh(U);

end;

Результат

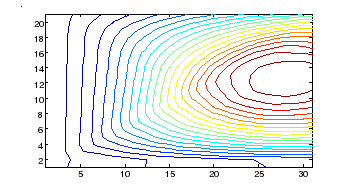
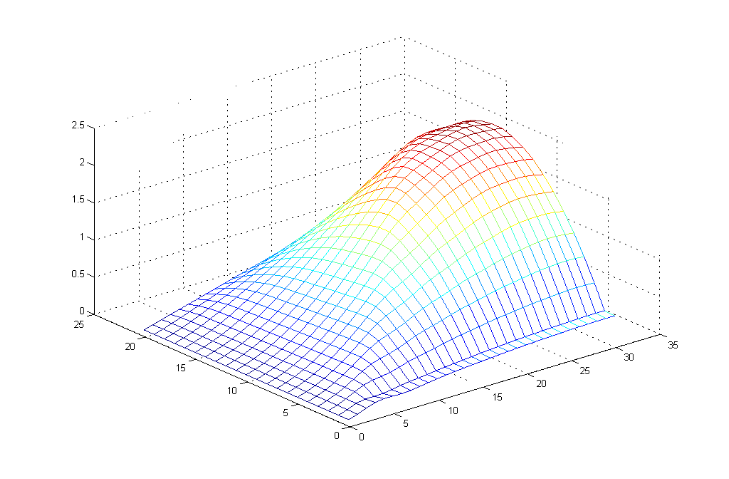
U [10x15]=

0 0.1430 0.3597 0.5587 0.6670 0.7004 0.7233 0.7682 0.8189 0.8498 0.8502

0 0.1490 0.3853 0.5224 0.5761 0.6361 0.7342 0.8255 0.8732 0.8888 0.8841

0 0.1462 0.3756 0.6908 0.9922 1.1891 1.3067 1.4270 1.5577 1.6248 1.5813

0 0.1422 0.3590 0.6569 1.0308 1.4268 1.7433 1.9199 1.9937 2.0273 2.0136

0 0.1377 0.3411 0.6180 0.9627 1.3599 1.7624 2.0810 2.2358 2.2310 2.1447

0 0.1331 0.3237 0.5734 0.8644 1.1743 1.4892 1.7954 2.0483 2.1728 2.1238

0 0.1288 0.2954 0.4854 0.6825 0.8831 1.0890 1.2991 1.5038 1.6725 1.7472

0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

Неявная схема

function neyav(M,N)

h=1/M; t=1/N;

u=zeros(M+1,N+1);

h2=h^2; t2=t^2;

g2=t2/h2;

for i=0:M

u(i+1,1)=0;

end;

A=zeros(M,1);C=zeros(M+1,1);B=A;A1=A;F=C;B1=C;

for i=1:M-1

A(i)=g2/2;

B(i+1)=g2/2;

C(i+1)=1+g2;

F(i+1)=t+5*t2/(1+h2*i^2);

end;

A(M)=0; B(1)=g2;

C(1)=1+h*g2+g2;

C(M+1)=1;

F(1)=t+5*t2;

F(M+1)=t;

A1(1)=B(1)/C(1);

B1(1)=F(1)/C(1);

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,2)=B1(M+1);

for i=M:-1:1

u(i,2)=A1(i)*u(i+1,2)+B1(i);

end;

for i=1:M-1

A(i)=g2;

B(i+1)=g2;

C(i+1)=1+2*g2;

end

A(M)=0;

B(1)=2*g2;

C(1)=1+2*h*g2+2*g2;

C(M+1)=1;

A1(1)=B(1)/C(1);

B1(1)=F(1)/C(1);

F(1)=t2*(t+5*t2);

for j=2:N

for i=1:M-1

F(i+1)=2*u(i+1,j)-u(i+1,j-1)+10*t2/(1+h2*i^2+t2*j^2);

end;

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

F(M+1)=j*t;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,j+1)=B1(M+1);

for i=M:-1:1

u(i,j+1)=A1(i)*u(i+1,j+1)+B1(i);

end;

end;

contour(u,20);pause;

for j=0:N,

i=1:1:M;

u1=u(i,j+1);

plot(i,u1);

end;

mesh(u);

end;

Результат

M=30, N=30

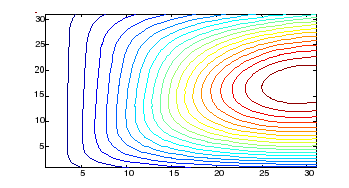
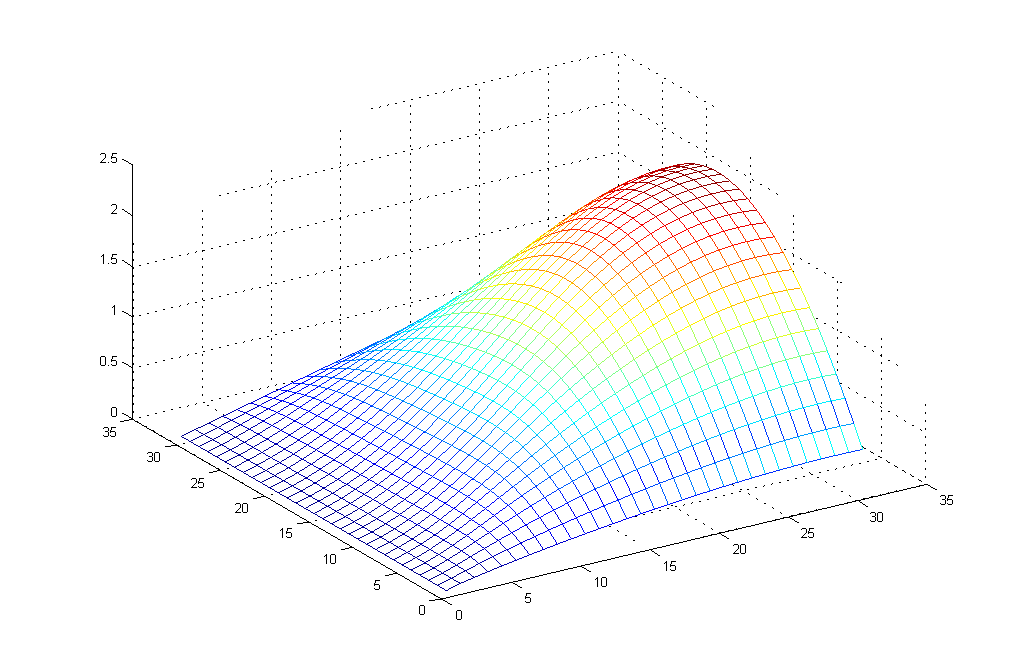
u[10x10] =

0 0.1414 0.2575 0.3850 0.5108 0.6285 0.7330 0.8200 0.8857 0.9269 0.9415

0 0.1469 0.3369 0.5410 0.7423 0.9305 1.0978 1.2370 1.3421 1.4080 1.4315

0 0.1471 0.3644 0.6200 0.8856 1.1401 1.3685 1.5594 1.7038 1.7950 1.8292

0 0.1454 0.3693 0.6489 0.9556 1.2611 1.5417 1.7789 1.9594 2.0748 2.1209

0 0.1429 0.3642 0.6489 0.9726 1.3064 1.6210 1.8918 2.1006 2.2367 2.2955

0 0.1399 0.3543 0.6320 0.9531 1.2906 1.6153 1.9002 2.1244 2.2750 2.3467

0 0.1366 0.3415 0.6038 0.9060 1.2248 1.5347 1.8113 2.0346 2.1912 2.2744

0 0.1331 0.3253 0.5641 0.8329 1.1135 1.3869 1.6350 1.8416 1.9944 2.0865

0 0.1288 0.3029 0.5076 0.7294 0.9564 1.1780 1.3829 1.5602 1.7005 1.7976

0 0.1210 0.2663 0.4240 0.5872 0.7518 0.9135 1.0672 1.2073 1.3287 1.4278

0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ :

1. В.Г. Долголаптев, В.Н. Земсков. Численные методы решения разностных уравнений математической физики. Методические указания к курсовой работе по высшей математике, МИЭТ 1987.

2. Сборник задач по математике. т.4 Методы оптимизации. Уравнения в частных производных. Интегральные уравнения. под ред. А.В. Ефимова, М. Наука 1990.

9