Классификация задач. Линейное уравнение второго порядка в частных производных в общем случае имеет вид:
(1)
где a,
b, c, d, e, g, f
- известные функции от x
и y.
Если a,
b, c, d, e, g
– константы, то (1) называется уравнением
с постоянными коэффициентами. Если f(x,
y)=0,
то уравнение является однородным.
Уравнение
(1) называется эллиптическим,
если D < 0;
гиперболическим,
если D > 0;
параболическим,
если D = 0.
D
- дискриминант квадратичной формы:
.
При помощи
невырожденного преобразования
уравнение
(1) можно привести к одному из следующих
канонических видов:
эллиптический
гиперболический
параболический
Постановка задачи. При математическом описании физического процесса надо, прежде всего, поставить задачу, т. е. сформулировать условия, достаточные для однозначного определения процесса. Дифференциальные уравнения имеют бесчисленное множество решений, поэтому для однозначного определения процесса необходимы также дополнительные условия краевые и начальные. Краевые и начальные условия зависят от типа уравнения.
Итак, в нашем случае
нам надо: получить приблизительное
решение краевой задачи уравнения в
частных производных математической
физики методом сеток:
(1)
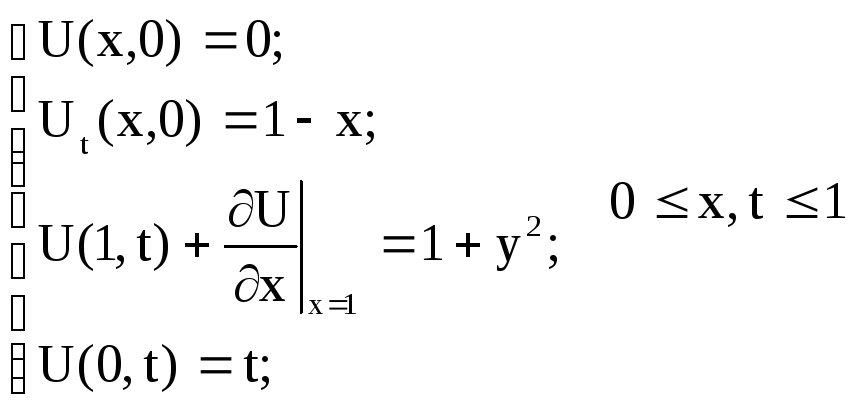(2).
Данное уравнение
является уравнением гиперболического
типа и физически отражает процесс
колебания струны. Искомое решение
U=U(x,t)
-
вертикальное
отклонение струны в точке х
в момент
времени
t.
Данная краевая задача состоит в нахождении
функции
U=U(x,t),
удовлетворяющей уравнению (1), а также
заданным начальным и граничным условиям
(2). Граничное условие первого рода
U=U(0,t)
определяет
закон движения левого конца струны. Для
правого конца в качестве граничного
условия задано так называемое условие
«упругого конца» (граничное условие
третьего рода):
U(1,t)=1+y
-Ux(1,t).
Начальные условия U(x,0)=0 и Ut(x,0)=1-x задают начальную форму струны и распределение скоростей в начальный момент времени. Функция f(x,t) имеет смысл плотности внешней силы, рассчитанной на единицу длины.
Решение задачи с помощью явной разностной схемы
В явной разностной схеме значение сеточной функции на последующем слое полностью определяется её значением на предыдущем слое по рекуррентным формулам. Для сведения задачи к явной разностной схеме используем шаблон "крест". (Выбор шаблона определяется стремлением получить наиболее эффективную для вычислений и устойчивую к ошибкам округления схему.) Получаем конечно-разностную систему:
,
с погрешностью
аппроксимации порядка
.
Обозначим
g=
/h
и выразим U(i,j+1)
через остальные значения сеточной
функции, входящие в уравнение:
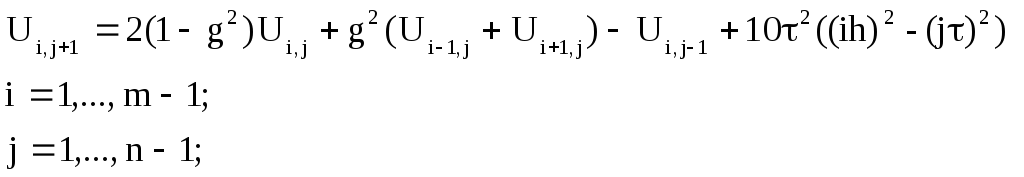(3)
Уравнение (3) должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями, получаемыми из аппроксимации краевых и начальных условий.
Аппроксимация 1-го начального условия даёт нам следующее:
(4)
Аппроксимация 1-го краевого условия (условие второго рода) используется только для нахождения решения на границе i=0 в явном виде:
(5)
Для
более точного аппроксимирования
2-го начального условия
(с погрешностью порядка
)
разложим функцию U(x,t)
в окрестности точки (x,0)
по формуле Тейлора:
.
Учитывая уравнение краевой задачи (1) и условие (2):
.
Перейдём к конечным разностям, записываемым в узле (i,1) (т.е. на первом временном слое):
(6).
Формула (6) используется на начальном этапе для вычисления значения функции U(x,t) на первом слое, по известным значениям функции на нулевом слое и на границе.
Принимая во внимание (4):
(7).
Для
более точного аппроксимирования
2-го граничного условия
(с погрешностью порядка
)
разложим
функцию
U(x,t)
в окрестности точки (1,t)
по формуле Тейлора:
Используя уравнение краевой задачи (1) и условие (2) получаем:
Перейдя к конечным разностям, записываемым в узле (m-1,j), получаем:
(8)
Выразим из (8)
:
(9)
Подставляя в (8) j=0 и учитывая (4), получаем:
(10)
Подставляя далее в (6) i=m и учитывая (4), получаем:
(11)
Из (3) при i=m, j=0, получим:
Учитывая (4) и подставляя сюда (11) и (10), находим:
(12)
Итак, объединяя полученные результаты, получаем аппроксимацию краевого условия третьего рода, т.е значение функции на границе i=m, в явном виде:
(9)
(12)
Устойчивость решения. Для уравнений гиперболического типа метод спектральных гармоник приводит к следующему
условию устойчивости:
(13),
т.е. если это условие
устойчивости не будет выполнено, то в
процессе рекуррентного решения возможно
накапливание ошибок от слоя к слою.
Отсюда, в частности, получаем для явной
схемы (
)
условие устойчивости Куранта-Леви:
.
Итак U(i,j) при j=0 и j=1 определены. Включается рекуррентная процедура описываемая уравнением (3) и вычисляется U(i,j) для всех i=1,2,...,m-1, для каждого фиксированного j=2,...,n-1. Далее приведена таблица значений функции для явной схемы (временная ось разбита на 25 отрезков, а ось стержня на 10), поверхность функции, являющейся решением нашего дифференциального уравнения и полученная с помощью явной разностной схемы (n=40; m=20), а также график 40 линий уровня (n=40; m=20).
-
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
0.0400
0.0361
0.0323
0.0287
0.0253
0.0220
0.0189
0.0159
0.0131
0.0105
0.0240
0.0800
0.0723
0.0653
0.0589
0.0531
0.0480
0.0435
0.0397
0.0365
0.0365
0.0909
0.1200
0.1087
0.0989
0.0905
0.0835
0.0780
0.0739
0.0713
0.0705
0.0840
0.1856
0.1600
0.1453
0.1331
0.1235
0.1165
0.1120
0.1101
0.1108
0.1168
0.1584
0.2901
0.2000
0.1820
0.1680
0.1580
0.1520
0.1500
0.1520
0.1586
0.1786
0.2598
0.3916
0.2400
0.2189
0.2035
0.1939
0.1901
0.1920
0.1998
0.2157
0.2599
0.3815
0.4870
0.2800
0.2559
0.2397
0.2313
0.2307
0.2380
0.2537
0.2843
0.3628
0.5128
0.5820
0.3200
0.2931
0.2765
0.2701
0.2739
0.2881
0.3145
0.3671
0.4862
0.6428
0.6855
0.3600
0.3305
0.3139
0.3103
0.3197
0.3425
0.3836
0.4668
0.6241
0.7659
0.8030
0.4000
0.3680
0.3520
0.3520
0.3681
0.4018
0.4632
0.5841
0.7678
0.8831
0.9330
0.4400
0.4057
0.3907
0.3951
0.4194
0.4669
0.5554
0.7167
0.9082
1.0003
1.0677
0.4800
0.4435
0.4301
0.4398
0.4738
0.5395
0.6620
0.8589
1.0398
1.1234
1.1978
0.5200
0.4815
0.4701
0.4861
0.5322
0.6215
0.7826
1.0027
1.1624
1.2543
1.3175
0.5600
0.5197
0.5108
0.5343
0.5957
0.7146
0.9140
1.1403
1.2801
1.3892
1.4270
0.6000
0.5580
0.5523
0.5850
0.6660
0.8196
1.0505
1.2669
1.3981
1.5207
1.5319
0.6400
0.5966
0.5949
0.6391
0.7447
0.9352
1.1847
1.3820
1.5192
1.6415
1.6379
0.6800
0.6354
0.6389
0.6980
0.8330
1.0577
1.3097
1.4887
1.6416
1.7486
1.7472
0.7200
0.6747
0.6850
0.7630
0.9308
1.1811
1.4214
1.5917
1.7595
1.8439
1.8565
0.7600
0.7147
0.7343
0.8355
1.0361
1.2987
1.5194
1.6938
1.8660
1.9324
1.9586
0.8000
0.7561
0.7880
0.9161
1.1446
1.4043
1.6065
1.7942
1.9566
2.0181
2.0469
0.8400
0.7995
0.8476
1.0040
1.2504
1.4944
1.6868
1.8882
2.0310
2.1014
2.1188
0.8800
0.8459
0.9138
1.0964
1.3471
1.5690
1.7630
1.9693
2.0928
2.1778
2.1766
0.9200
0.8965
0.9866
1.1888
1.4294
1.6308
1.8345
2.0326
2.1463
2.2410
2.2255
0.9600
0.9518
1.0645
1.2752
1.4944
1.6833
1.8974
2.0767
2.1934
2.2860
2.2697
1.0000
1.0119
1.1439
1.3497
1.5424
1.7292
1.9457
2.1039
2.2322
2.3118
2.3092