ЧМ (МП-3) / Курсовые / mpm_16b / berry_16

Московский Государственный Институт Электронной Техники

(Технический Университет)

Курсовая работа

по курсу

“Методы прикладной математики”

на тему

“Приближённое решение краевых задач математической физики методом сеток”.

Выполнила: Хлызова О.В.

гр. МП - 39 Проверил:Умняшкин .

Москва

2000 г.

Методические указания и постановка задачи.

1. Тема.

Приближенное решение краевых задач математической физики методом сеток.

2. Цель работы.

Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональной ЭВМ в среде MATLAB. Преимущество использования этой среды — богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.

3. Порядок работы.

1. Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу. Наиболее полно все основные понятия метода сеток изложены в [1,2]. Достаточной теоретической базой может служить методическое пособие [3].

2. Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.

3. Разобраться с методикой построения явных и неявных разностных схем конечно-разностных систем для данного типа уравнения.

4. Разобраться с устойчивыми методами решения явной и неявной схем.

5. Реализовать программу, осуществляющую решение в среде MATLAB.

6. Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.

7. Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части должны быть кратко освещены следующие вопросы:

• Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.

• Корректная постановка: граничные и начальные условия и их соответствие физическому смыслу.

• Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.

• Выбор шагов сетки и оценка погрешности метода.

Порядок выполнения работы.

1. Классификация краевой задачи и её физический смысл

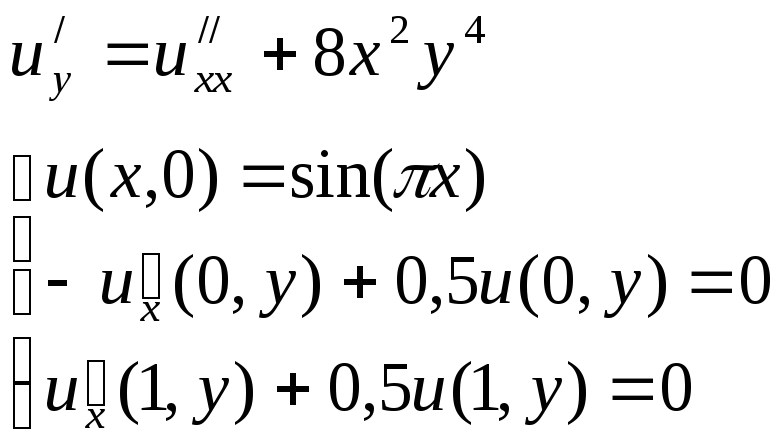
Линейное дифференциальное уравнение второго порядка такого вида относится к уравнениям параболического типа. Данное уравнение описывает распределение тепла в однородном стержне единичной длины в зависимости от времени.

В данной задаче начальные и граничные условия имеют следующий смысл. Начальное условие задает распределение температуры на всем стержне в момент времени t=0. Граничное условие 3-го рода говорит о том, что на левом конце стержня по закону Ньютона происходит теплообмен с окружающей средой. Граничное условие 3-го рода говорит о том, что на правом конце стержня по закону Ньютона происходит теплообмен с окружающей средой.

Решение сеточного уравнения.

Явная разностная схема.

В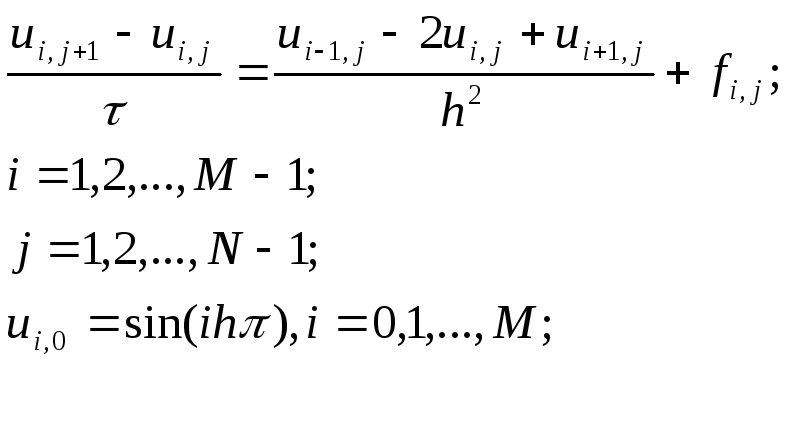 явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекурентным формулам. В данной задаче апроксимацию дифференциальных операторов проведём по следующему шаблону :

Тогда конечно-разностная схема для данной задачи имеет вид :

З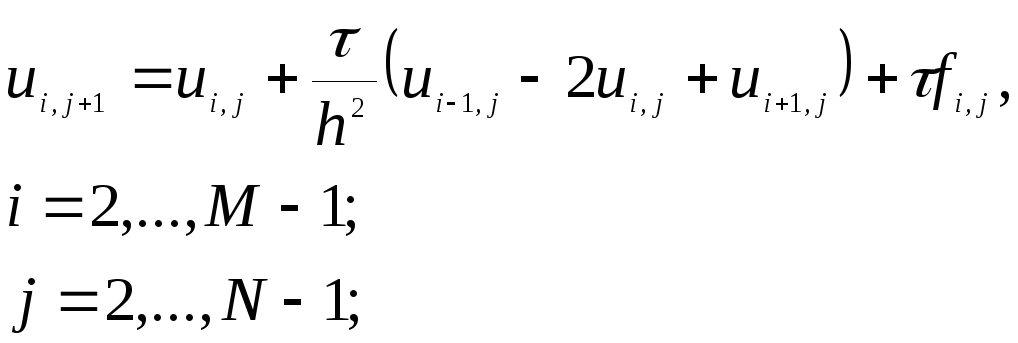 начение температуры на слое явно выражается через значение температуры на слое по формуле :

П орядок аппроксимации данной разностной схемы равен . Для получения , разложим в окрестности точки по формуле Тейлора :

И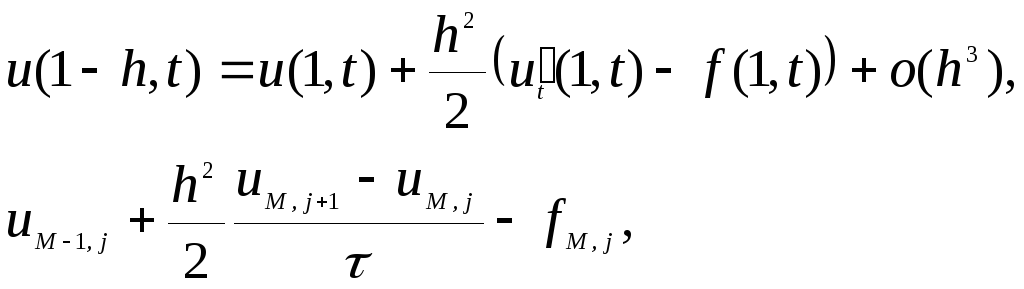 спользуя граничное условие третьего рода , получим

Практическая реализация данного метода возможна лишь при таких соотношениях между шагами сетки и , при которых выполняется условие устойчивости решения к ошибкам округления и неточностям в начальных данных. Это условие имеет вид . Текст функции, вычисляющий матрицу решения размерностью приведён ниже.

function result=yavn(M)

disp('-----------------=* Yavn *=-------------');

disp('-------------=* Hlyzova O.V.=*-------------')

pause;

N = 3*M^2

h=1/M;

t=1/N;

U=zeros(M+1,N+1);

for X=1:M+1,

U(X,1)=sin(pi*(X-1)*h);

end

for J=1:N,

y=(J-1)*t;

U(1,J+1)=2*t/h^2*(U(2,J)-U(1,J)*(1+h/2-h^2/(2*t)));

U(M,J+1)=2*t/h^2*(U(M+1,J)+U(M,J)*(1+h/2-h^2/(2*t)))+t*8*h^2*y^4;

for X=2:M,

x=(X-1)*h;

U(X,J+1)=U(X,J)+t/h^2*(U(X-1,J)-2*U(X,J)+U(X+1,J))+t*(8*x^2*y^4);

end

end

mesh(0:(1/N):1,0:(1/M):1,U),grid;

result=U;

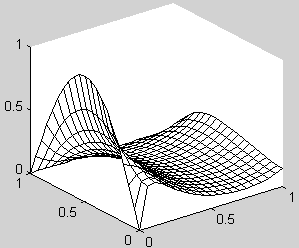
Результат явной разностной схемы показан на графике:

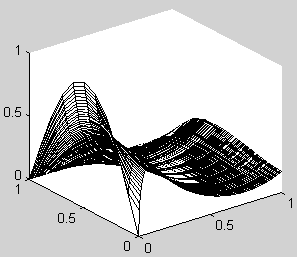
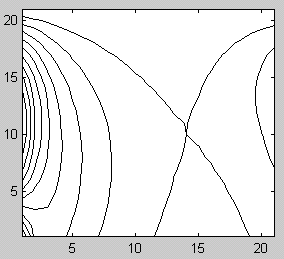
Линии уровня:

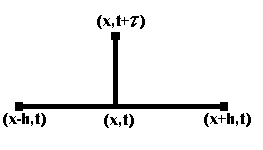
Выбор сеточного шаблона для неявной разностной схемы

x

t

Рисунок 1

Для простоты вычислений воспользуемся прямоугольной равномерной сеткой с (N+1) узлом на оси OX и (M+1) на оси OY. На данной сетке заменим частные производные разностными операторами и введём сеточную функцию у которая соответствует функции u из пространства непрерывных функций.

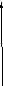
Для решения задачи с применением неявной разностной схемы воспользуемся Т-образным шаблоном, изображенным на рисунке 1.

1. Аппроксимируем начальное условие :

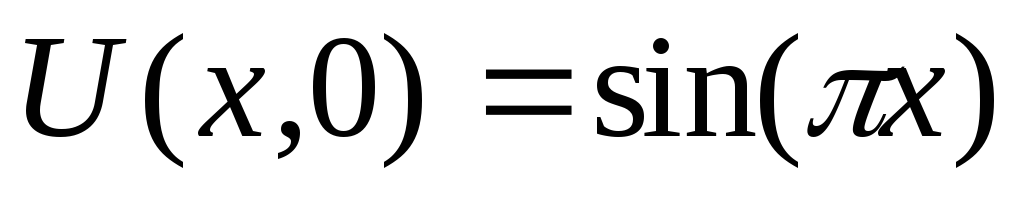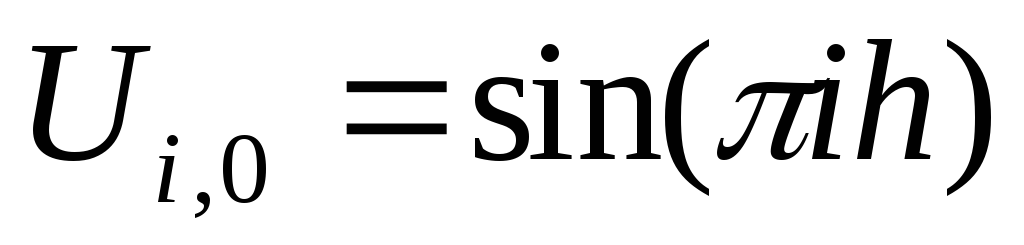
2. Аппроксимация граничного условия третьего рода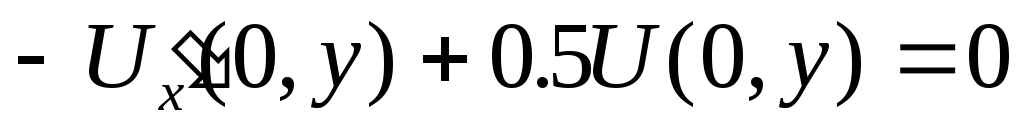: Производную заменяем левой разностной производной: 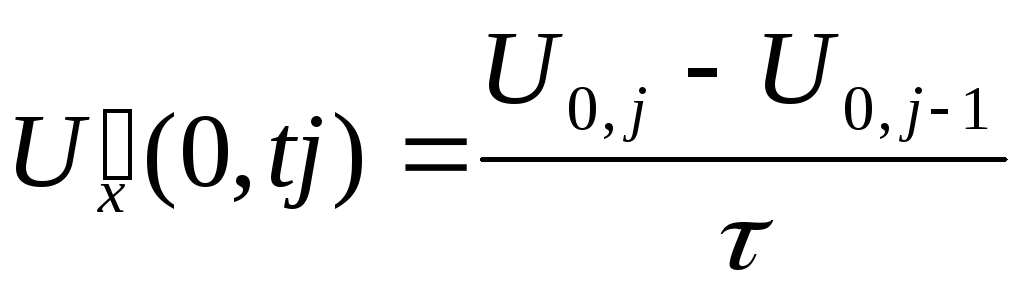. Записывая краевое условие третьего рода в узле (0, tj) и подставляя сюда производную получим в итоге:

3. Аппроксимация второго граничного условия третьего рода происходит аналогично, и из-за схожести граничных условий они отличаются только знаками при коэффициенте :

Перепишем все неравенства в систему, удобную для применения метода прогонки:

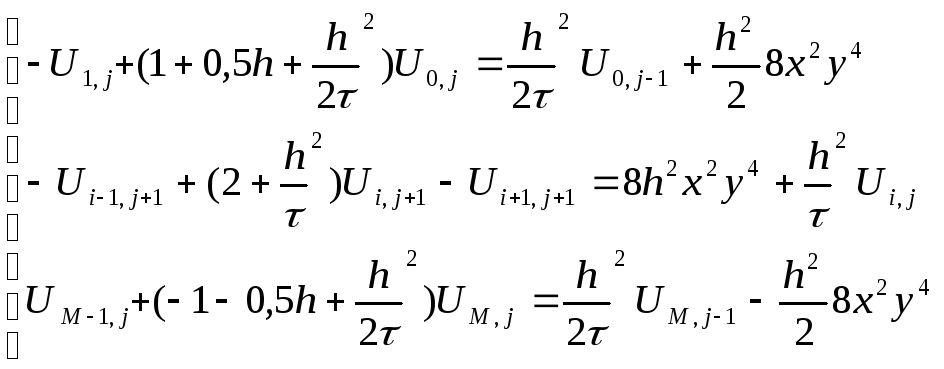
Прогоночные коэффициенты:

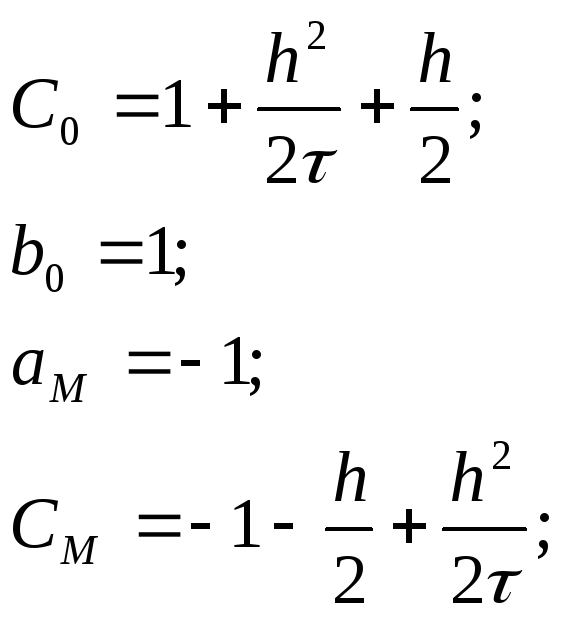
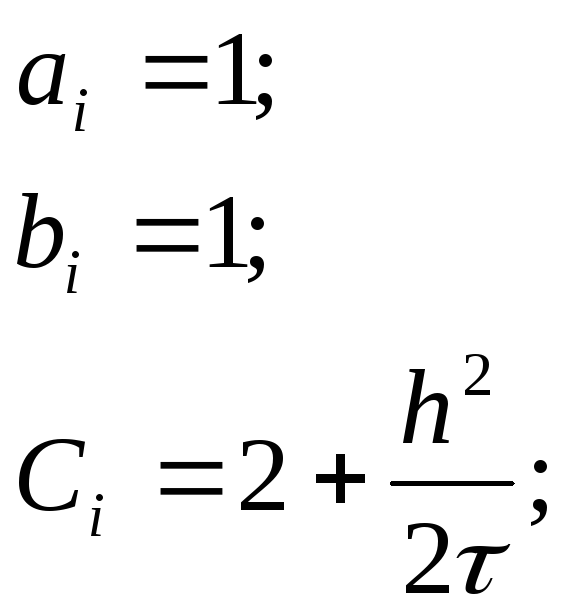
Текст программы для неявной схемы:

disp('_________________________________________________________________');

disp(' Neyavn')

disp(' Hlyzova O.V. v.16')

disp('_________________________________________________________________');

M = input('Enter M:');

N = input('Enter N:');

h=1/M;

t=1/N;

c(1)=1+h^2/(2*t)+0.5*h;

for i=2:M,

c(i)=2+h^2/t;

end

c(M)=1+h^2/(2*t)-0.5*h;

b(1)=1;

a(M)=-1;

for i=2:M,

b(i)=1; end

for i=2:M,

a(i)=1; end

alfa(1)=b(1)/c(1);

for i=2:M,

alfa(i)=b(i-1)/(c(i-1)-a(i-1)*alfa(i-1)); end

alfa(M+1)=c(M+1)/a(M+1);

U=zeros(M+1,N+1);

for X=1:M+1,

x = (X-1)*h;

U(X,1) = sin(pi*x);

end

for T=2:N+1,

y=(T-1)*t;

f(1)=0;

for i=2:M,

x=(i-1)*h;

f(i)=h^2*(8*x^2*y^4)+h^2/t*U(i-1,T-1);

end

f(M)=h^2/(2*t)*U(M,T-1)+h^2/2*(8*x^2*y^4);

betta(1)=f(1)/c(1);

for i=2:M,

betta(i)=(f(i-1)+a(i-1)*betta(i-1))/(c(i-1)-a(i-1)*alfa(i-1));

end

U(M,T)=betta(M+1);

for i=M:-1:1,

U(i,T)=U(i+1,T)*alfa(i)+betta(i);

end

end

mesh(0:1/(N):1,0:1/(M):1,U),grid;

result=U;

Устойчивость решения неявной схемы.

Как известно из теоремы, для того, чтобы решение системы неявным методом было устойчивым необходимо, чтобы выполнялись следующие условия для коэффициентов системы решения:

1. , , ,

2. 

3. ,

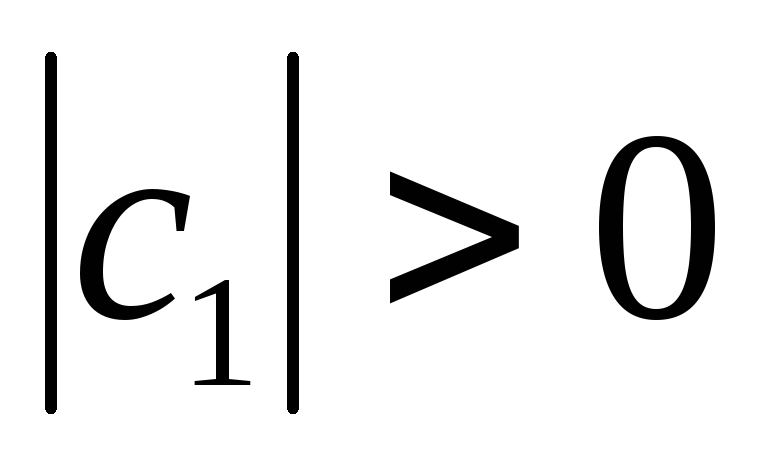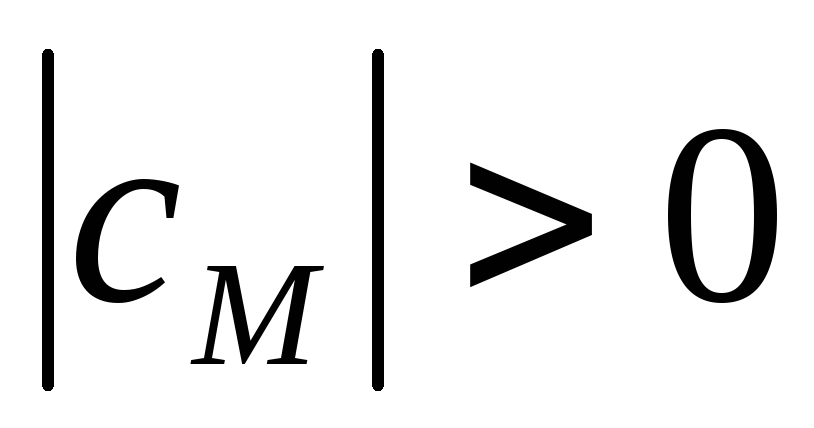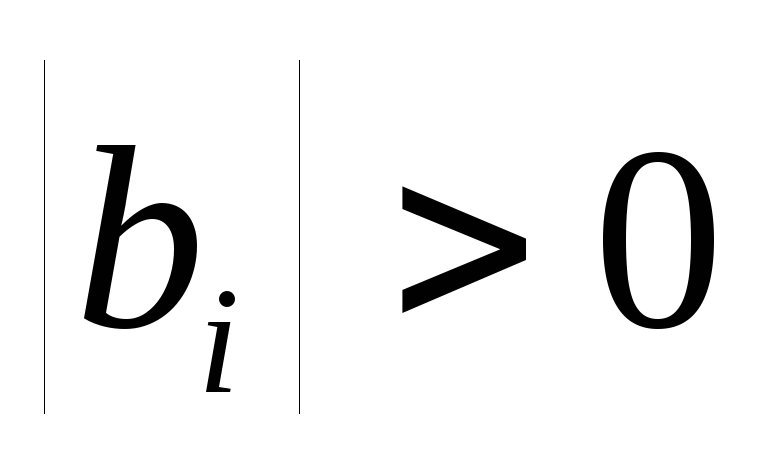
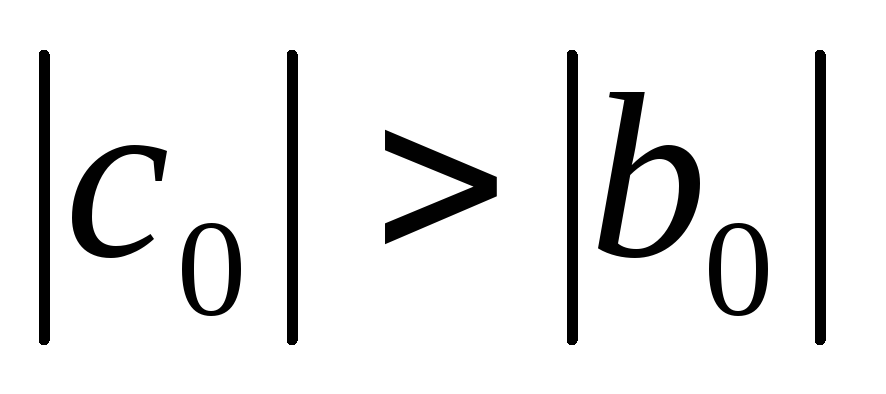Если же посмотреть на решение системы, то видно, что выполняются все вышеприведенные условия, что и доказывает, что решение системы устойчиво.

Результат неявной разностной схемы показан на графике:

Л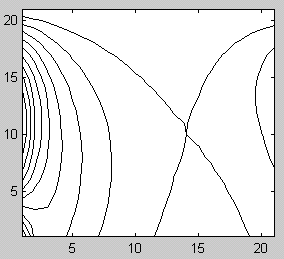 инии уровня:

Список литературы

1. Теория разностных схем., Самарский А. А., М., Наука, 1977г.

2. Численные методы., Калиткин Н. Н., М., Наука, 1978г.

3. Численные методы решения разностных уравнений мат физики. Долголаптев В. Г., Земсков В. Н., М., МИЭТ, 1987г.

4. Сборник задач по математике для втузов, т. 4 Методы оптимизации, М., Наука, 1990г.

5. Методическое пособие по выполнению домашних заданий с использованием ЭВМ “Решение уравнений математической физики методом сеток”, М., МИЭТ, 1976г.

6. Методы решения сеточных уравнений., Самарский А. А., Николаев Е. С., М., Наука, 1978г.

7. Прикладные итерационные методы. Хейгеман Л., Янг Л., М., Мир, 1986г.

8. Матрицы и вычисления., Воеводин В. В., Кузнецов Ю. А., М., Наука, 1984г.

0