От Шатохина_Статиститка. Орлов, Айвазян / Лекции с прошлого семестра / Лекция № 10

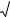
где а и S2 – параметры закона, интерпретируемые соответственно как среднее значение и дисперсия данной случайной величины (в виду особой роли нормального распределения мы будем использовать специальную символику для обозначения его функции плотности и функции распределения).

Соответствующая функция распределения нормальной случайной величины X(а, S2) обозначается Ф (х; а, S2)

и задается соотношением

Условимся называть нормальный закон с параметрами а = 0 и S2 = 1 стандартным, а его функции плотности и распределения обозначать соответственно φ(x) = φ(x; 0,1) и Ф(x) = Ф(x; 0,1).

Во многих случайных величинах, изучаемых в экономике, технике, медицине, биологии и в других областях, естественно видеть суммарный аддитивный эффект большого числа независимых причин. Но центральное место нормального закона не следует объяснять его универсальной приложимостью, как это было принято долгое время (по-видимому, под влиянием блестящих работ К. Гаусса и П. Лапласса).

В этом смысле нормальный закон – это один из многих типов распределения, имеющихся в природе, правда, с относительно большим удельным весом практической приложимости.

И потому нам понятна ирония, звучащая в известном высказывании Липмана (цитируемом А. Пуанкаре в своем труде «Исчисление вероятностей», Париж, 1912 г.):

«Каждый уверен в справедливости нормального закона: экспериментаторы – потому, что они думают, что это математическая теорема; математики – потому, что они думают, что это экспериментальный факт».

Однако не следует упускать из виду, что полнота теоретических исследований, относящихся к нормальному закону, а также сравнительно простые математические свойства делают его наиболее привлекательным и удобным в применении.

Даже в случае отклонения исследуемых экспериментальных данных от нормального закона существует по крайней мере два пути его целесообразной эксплуатации:

а) использовать его в качестве первого приближения; при этом нередко оказывается, что подобное допущение дает достаточно точные с точки зрения конкретных целей исследования результаты;

б) подобрать такое преобразование исследуемой случайной величины X, которое видоизменяет исходный «не нормальный» закон распределения,

X(i) при фиксированном значении другой компоненты (X(j) = x(j)) снова описывается нормальным законом, параметр среднего значения которого, как и следовало ожидать, зависит от фиксированного значения x(j):

E(X(i) | X(j) = x(j)) = m1(i ) + r σσ ii (x(j) – m1( j ) ),

jj

и дисперсия которого не зависит от x(j) и равна

D(X(i) | X(j) = x(j)) = Sii(1 – r 2 ).

Многомерный нормальный закон описывает совместное распределение p-мерной случайной величины X = (X(1), X(2),... , X(p)) с непрерывными компонентами X(j), механизм формирования значений каждой из которых тот же, что и в одномерном случае, причем множества случайных факторов, под воздействием которых формируются значения X(1), X(2),... , X(p), вообще говоря, пересекаются (отсюда их возможная взаимозависимость).

Задавшись p-мерным вектор-столбцом М1 средних значений компонент и (р´p)-матрицей ковариации Σ, можно выписать p-мерную совместную плотность многомерного нормального закона:

переменных, а Σ = det( Σ ) – определитель ковариационной матрицы.

Вырожденность матрицы Σ (т. е. равенство нулю определителя Σ )

делает соответствующее многомерное распределение вырожденным (или несобственным); это означает, в частности, что разброс значений исследуемого многомерного признака сосредоточен в подпространстве меньшей, чем p, размерности. За исключением некоторых специальных случаев мы всегда будем полагать, что нами уже осуществлен переход в это подпространство меньшей размерности, так что в наших рассуждениях

предполагается Σ > 0.

3. Логарифмически-нормальное распределение.

Случайная величина η называется логарифмически-нормально распределенной, если ее логарифм (ln η) подчинен нормальному закону

распределения.

Это означает, в частности, что значения логарифмически-нормальной случайной величины формируются под воздействием очень большого числа взаимно независимых факторов, причем воздействие каждого отдельного фактора «равномерно незначительно» и равновероятно по знаку. При этом в отличие от схемы формирования механизма нормального закона последовательный характер воздействия случайных факторов таков, что случайный прирост, вызываемый действием каждого следующего фактора, пропорционален уже достигнутому к этому моменту значению исследуемой величины (в этом случае говорят о мультипликативном характере воздействия фактора).

Математически сказанное может быть формализовано следующим образом. Если η0 = а – неслучайная компонента исследуемого признака η (т. е. как бы «истинное» значение η в идеализированной схеме, когда устранено влияние всех случайных факторов), a X1, X2,... , XN – численное выражение эффектов воздействия упомянутых выше случайных факторов, то последовательно трансформированные действием этих факторов значения исследуемого признака будут:

η1 = η0 + X1·η0;

η2 = η1 + X2·η1;

………………..

ηN = ηN-1 + XN·ηN-1.

Отсюда получаем, что

множества случайных факторов, что при сделанных выше предположениях должно приводить к нормальному распределению этой суммы. В то же время, учитывая достаточную многочисленность числа случайных слагаемых (т. е. полагая N Ø ¶) и относительную незначительность воздействия каждого из них (т. е. полагая óηi Ø 0), можно от суммы в левой части (7) перейти к интегралу

Это и означает в конечном счете, что логарифм интересующей нас величины (уменьшенный на постоянную величину ln а) подчиняется нормальному закону с нулевым средним значением, т. е.

откуда дифференцированием по x левой и правой частей этого соотношения получаем

(правомерность использованного при вычислении fη(x) тождества

P{η < x} = P{ln η < ln x}

вытекает из строгой монотонности преобразования ln η).

Указанная схема формирования значений логарифмически-нормальной случайной величины оказывается характерной для многих конкретных физических и социально-экономических ситуаций:

∙размеры и вес частиц, образующихся при дроблении;

∙заработная плата работника;

∙доход семьи;

∙размеры космических образований;

∙долговечность изделия, работающего в режиме износа и старения и

др.

Пример 1. В качестве случайной величины η рассматривается душевой месячный доход (в долларах) семьи некоторой совокупности семей. Обследовано п = 750 семей.

Втабл. 1 и 2 приведены результаты группировки выборочных данных ( xi )

иих логарифмов (ln x i ) соответственно (ширина интервала группирования равна 25 долларам).

На рис. 1, а, б изображены гистограммы и плотности соответственно логарифмически-нормального и нормального законов распределения.

Таблица 1.

Таблица 2.

Рис. 1, а, б. Гистограмма и теоретическая (модельная) плотность,

характеризующие распределение семей по среднедушевому месячному доходу ( а) и по логарифму среднедушевого месячного дохода ( б)