
От Шатохина_Статиститка. Орлов, Айвазян / Лекции с прошлого семестра / Лекция № 11
.pdf
Лекция № 11. Равномерное экспоненциальное распределение.
Содержание
1.Равномерное (прямоугольное) распределение.
2.Распределение Вейбулла и экспоненциальное (показательное).
1. Равномерное (прямоугольное) распределение.
Случайная величина X называется равномерно распределенной на отрезке [а, b], если ее плотность вероятности fX(x) постоянна на этом отрезке и равна нулю вне его, т. е.
|
1 |
при a ≤ x ≤ b; |
|
|
|
|
||
fξ (x) = b − a |
(1) |
|
< >0 при x a и x b.
Так как график функции fX(x) изображается в виде прямоугольника (см. рис. 1), то такое распределение также называют
прямоугольным.
Рис. 1. Функция плотности равномерной случайной величины (fX(x)) и суммы двух (fX(x)) и трех (fX(x)) независимых равномерно распределённых на [0, 1] случайных величин
Соответственно функция распределения FX(x) равномерного закона задается соотношениями:
|
|
|
|
|
0 при x ≤ a; |
|
|
||
|
|
|
|
|
x − a |
|
|
|
|
Fξ (x) = |
|
при a |
< x ≤ b; |
(2) |
|
||||
b − a |
|
|
||
1 при x > b. |
|
|
||
|
|
|
|
|
Примерами реальных ситуаций, связанных с необходимостью
рассмотрения равномерно распределенных случайных величин, могут служить:
∙анализ ошибок округления при проведении числовых расчетов
(такая ошибка, как правило, оказывается равномерно распределенной на интервале от –5 до +5 единиц округляемого десятичного знака);
∙время ожидания «обслуживания» при точно периодическом, через каждые Т единиц времени, включении (прибытии) «обслуживающего устройства» и при случайном поступлении (прибытии) заявки на обслуживание в этом интервале.
Примером такого распределения является время ожидания пассажиром прибытия поезда метро при условии точных двухминутных интервалов движения метро и случайного момента появления пассажира на платформе будет распределено приблизительно равномерно на интервале [0 мин, 2 мин].
Отметим еще две важные ситуации, в которых используется равномерный закон.
Во-первых, в теории и практике статистического анализа данных широко используется вспомогательный переход от исследуемой случайной величины X с функцией распределения F(x ) к случайной величине η = F(X), которая оказывается равномерно распределенной на отрезке [0, 1].
Этот прием является полезным при статистическом моделировании наблюдений, подчиненных заданному закону распределения вероятностей, при построении доверительных границ для исследуемой функции распределения и в ряде других задач математической статистики.
Во-вторых, равномерное распределение иногда используется в качестве «нулевого приближения» в описании априорного распределения анализируемых параметров в так называемом байесовском подходе в условиях полного отсутствия априорной информации об этом распределении.
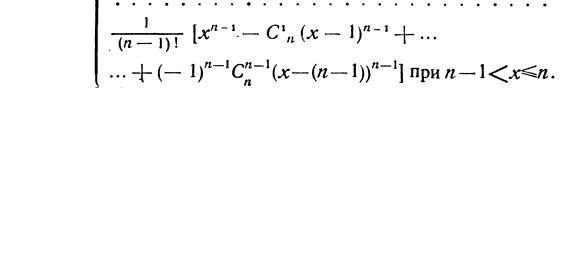
Числовые характеристики равномерного закона:
среднее, медиана ЕX = хтed = |
a + b |
; |
||
|
||||
|
|
2 |
|
|
дисперсия DX = |
(b − a)2 |
; |
|
|
|
|
|
||
12 |
|
|
|
|
асимметрия β1 = 0;
эксцесс β2 = –1, 2.
Отметим в заключение одно важное свойство суммы п независимых равномерно распределенных случайных величин: распределение этой суммы очень быстро (по мере роста числа слагаемых) приближается к нормальному закону.
В частности, если Xi – равномерно распределенные на отрезке [0, 1] и независимые случайные величины, то можно показать, что
плотность fηn (x) случайной величины ηn = X1 + X2 +...+ Xn имеет вид
(область возможных значений случайной величины ηn, очевидно, задается отрезком [0, п]).
Геометрическое изображение последовательного изменения вида плотности fηn (x) по мере роста числа слагаемых п (для п = 1, 2, 3)
дано на рис. 1.
Это свойство используется, в частности, при статистическом моделировании нормально распределенных наблюдений.
2. Распределение Вейбулла и экспоненциальное (показательное).
Рассмотрим один общий механизм формирования распределений, относящийся, в частности, к случайным величинам, характеризующим длительность жизни элемента, сложной системы или индивидуума (задачи теории надежности, анализ коэффициентов смертности в демографии и т. п.).
Пусть X – время жизни анализируемого объекта (системы, индивидуума) и F(t) =P{X < t} – его функция распределения, которую мы полагаем непрерывной и дифференцируемой.
В задачах данного профиля важной характеристикой является интенсивность отказа (коэффициент смертности) L(t)
исследуемых элементов возраста t, определяемая соотношением
λ(t) = - |
|
fξ (t) |
» |
n(t) - n(t + Dt) |
|
|
|
|
|
, |
(3) |
||
|
- Fξ (t) |
|
||||
1 |
|
Dt × n(t) |
|
|||
где п(t ) – число объектов, «доживших» до возраста t, а ót – достаточно малый отрезок времени. Это означает, что статистически (экспериментально) интенсивность отказа (коэффициент смертности) определяется как отношение удельного числа (т. е. приходящегося на единицу времени) «выбывших» в возрасте t элементов к общему числу доживших до этого возраста элементов
п(t ).
Справедливость приближенного равенства (3) вытекает из соотношения
|
|
[n - n(t + Dt)] -[n - n(t)] |
|
^ |
|
|||||
n(t) - n(t + Dt) |
|
|
|
|
|
|
|
|
fξ( n) (t) |
|
= |
|
|
Dt × n |
= |
, |
|||||
Dt × n(t) |
|
|
n - (n - n(t)) |
^ |
||||||
|
|
|
|
|
||||||
|
|
|
|
1 - F ( n) (t) |
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
|
ξ |
|
||
|
|
|
|
|
|
|
|
|||
где п – общее число «прослеживаемых» во времени (начиная с t = 0) элементов одинакового возраста, а (п – п(t)) – число тех из них, которые не дожили до возраста t (соответственно отношение
(п – п(t))/n определяет относительную частоту события {X < t}).
Разрешая уравнение (3) относительно функции распределения FX (t), получаем
t |
λ(t )dt |
−∫ |
|
Fξ (t) =1 − e 0 |
(4) |
Таким образом, конкретизация вида функции распределения
FX (t) полностью определяется видом функции интенсивности отказов (временной зависимостью коэффициентов смертности) L(t).
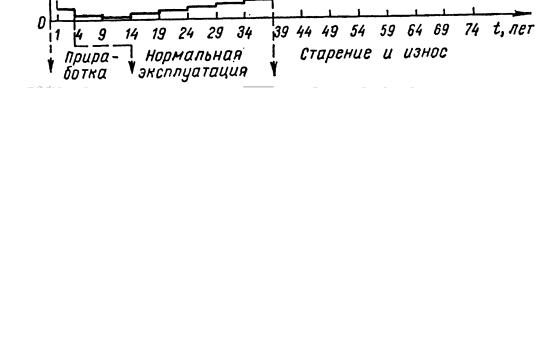
Многочисленные экспериментальные данные (и в области демографии, и в области анализа надежности технических элементов и систем) показывают, что в широком классе случаев функция L(t) имеет характерный вид кривой, изображенной на рис. 2. Из этого графика видно, что весь интервал времени можно разбить на три периода.
Рис. 2. Типичное поведение кривой смертности (интенсивности
отказов) и реальная (ступенчатая) кривая, описывающая изменение коэффициента смертности мужского населения Франции по данным 1955 г.
На первом из них функция L(t) имеет высокие значения и явную тенденцию к убыванию.
На техническом языке это можно объяснить наличием в исследуемой совокупности элементов с явными и скрытыми дефектами (сборки, некондиционности отдельных свойств и т. п.), которые приводят к относительно быстрому выходу из строя этих элементов.
Этот период принято называть периодом «приработки» (или
«обкатки»).
Затем наступает период нормальной эксплуатации, характеризующийся приблизительно постоянным и сравнительно низким уровнем «смертности» элементов.
Природа смертей (или «отказов») в этот период носит внезапный характер (аварии, несчастные случаи и т. п.) и не зависит от возраста объекта.
И наконец, последний период жизни (или эксплуатации)
элемента – период старения и износа.
Природа «отказов» в этот период – в необратимых физиологических или физико-химических явлениях, приводящих к ухудшению качества элемента, к его «старению».
Ниже абстрактной кривой на рисунке построена реальная ступенчатая кривая, описывающая изменение коэффициента смертности мужского населения Франции по данным 1955 г.
По оси ординат отложено количество умерших, приходящееся на 1000 человек данного возраста. В соответствии с этой кривой смертности периоду «приработки» соответствует возраст от 0 до 4
лет, периоду «нормальной эксплуатации» – от 4 до 39 лет, а
периоду «старения» – возраст после 39 лет.
Каждому периоду соответствует свой вид функции L(t), а следовательно, и свой закон распределения времени жизни X.
Рассмотрим класс степенных зависимостей, описывающих поведение L(t), а именно
λ(t) = λ ×α ×tα−1 |
, |
(5) |
0 |
|
|
где L0 > 0 и A > 0 – некоторые числовые параметры. Очевидно, значения A < 1, A = 1 и A > 1 отвечают поведению функции интенсивности отказов соответственно в период приработки,
нормальной эксплуатации и старения.
Подставляя (5) в (4), получаем вид функции распределения FX (t) времени жизни X элемента:
F (t) = 1- e−λ0tα |
, t ³ 0. |
(6) |
ξ |
|
|
Соответственно плотность вероятности
f |
ξ |
(t) = λ ×α ×tα−1 |
×e−λ0tα |
, t ³ 0. |
(7) |
|
0 |
|
|
|
Это и есть распределение Вейбулла. К тому же самому типу распределения можно прийти, отправляясь от широкого класса различных вероятностных законов и интересуясь распределением крайних членов их вариационных рядов.
Основные числовые характеристики распределения Вейбулла:
среднее ЕX = λ0 |
− |
1 |
× Г(1+ |
1 |
) ; |
||||||||
α |
|||||||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
α |
||
|
|
0, если α £ 1; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
мода |
xmcd |
= λ− |
1 |
(1 - |
1 |
) |
1 |
, если α ³ 1; |
|||||
α |
α |
||||||||||||
|
|
|
|||||||||||
|
|
0 |
|
|
|
α |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
− |
2 |
|
|
2 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
дисперсия DX = λ0 α |
× |
Г(1+ |
|
) - Г |
|
(1+ |
|
|
) |
; |
|
|
|
|||
α |
|
α |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
момент к-го порядка mk = ЕXk = λ0 |
− |
k |
|
|
|
|
|
k |
||||||||
α × |
Г 1 |
+ |
|
|
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
(здесь Г(z) – так называемая гамма-функция Эйлера, т.е.
∞
Г(z) = ∫xz−1e−xdx
0
Экспоненциальное (показательное) распределение хотя и является частным случаем распределения Вейбулла (когда L0 = 1), но, безусловно, представляет большой самостоятельный интерес.
Из вышесказанного следует, что оно адекватно описывает распределение длительности жизни элемента, работающего в режиме нормальной эксплуатации.
Экспоненциальный закон (и только он) обладает, в частности, тем важным свойством, что вероятность безотказной работы элемента на данном временном интервале (t, t +ó) не зависит от времени предшествующей работы t, а зависит только от длины интервала ó.
Экспоненциально распределенную случайную величину можно интерпретировать также как промежуток времени между двумя последовательными наступлениями «пуассоновского» события.
Прикладная популярность экспоненциального закона объясняется не только разнообразными возможностями его естественной физической интерпретации, но и исключительной простотой и удобством его модельных свойств. Ниже приводятся его функция распределения и плотность вероятности, а также его
основные числовые характеристики:

Fξ (x) =1 - e-λ0 x , x ³ 0; fξ (x) = λ0e-λ0 x , x ³ 0;
1 cреднее ЕX = λ0 ;
mода хтоd = 0;
1
медиана хтed = λ0 ln 2; ;
1
дисперсия DX = λ20 ; ;
асимметрия β1 = 2;
эксцесс β2 = 6.
Двустороннее экспоненциальное распределение (распределение Лапласа).
Симметричная унимодальная функция плотности этого закона с «острым» максимумом в точке х = 0 часто используется для описания распределения остаточных случайных компонент («ошибок») в линейных моделях.
График этой функции плотности представляет собой как бы результат «склеивания» графика показательного распределения со своим зеркальным – относительно вертикальной оси – отражением (с учетом необходимой нормировки), так что уравнение функции плотности имеет вид
f (x) = 1 λ × e-λ× x , (-¥ < x < ¥). 2
Нетрудно подсчитать основные числовые характеристики этого закона распределения:
cреднее ЕX = 0;
mода хтоd = 0;
медиана хтed = 0;

2
дисперсия DX = λ2 ; ;
асимметрия β1 = 0;
эксцесс β2 = 3.
