
От Шатохина_Статиститка. Орлов, Айвазян / Лекции с прошлого семестра / Лекция № 9
.pdfМодели законов распределения вероятностей, наиболее распространённые в практике статистических исследований.
Лекция № 9. Биномиальные распределения и распределение Пуассона.
Содержание.
1.Распределения, возникающие при анализе последовательности испытаний Бернулли: биномиальное и отрицательное биномиальное.
2.Гипергеометрическое распределение.
3.Распределение Пуссона.
Говоря о том, насколько распространена та или иная модель распределения в практике статистических исследований, следует иметь в виду две возможные роли, которые эта модель может играть.
Первая из них заключается в адекватном описании механизма исследуемого реального процесса, индуцирующего подлежащую статистическому анализу генеральную совокупность.
В этом случае выбранная по тем или иным соображениям (или выведенная теоретически) модель описывает закон распределения
вероятностей непосредственно анализируемой и имеющей четкую физическую интерпретацию случайной величины:
заработной платы работника,
дохода семьи,
числа сбоев автоматической линии в единицу времени,
числа дефектных изделий, обнаруженных в проконтролированной партии заданного объема,
ит. д..
Подходы к построению таких моделей, методы их анализа и обоснования относятся к области «реалистического» (или содержательного)
моделирования.
Другая роль широко распространенных в статистических исследованиях моделей – использование их как вспомогательное техническое средство
при реализации методов статистической обработки данных.
С помощью моделей этого типа описываются распределения вероятностей некоторых вспомогательных функций от исследуемых
случайных величин, используемых для построения разного рода статистических оценок и статистических критериев.
К распределениям этого типа относятся в первую очередь распределения «хи-квадрат», Стьюдента (t-распределение) и F-распределение.
1. Распределения, возникающие при анализе последовательности
испытаний Бернулли: биномиальное и отрицательное биномиальное.
Широкий класс случайных величин, которые приходится изучать в практике статистических исследований, индуцируется последовательностью независимых случайных экспериментов следующего типа:
∙в результате реализации каждого случайного эксперимента (наблюдения) некоторое интересующее нас событие А может произойти (с некоторой вероятностью р) или не произойти (соответственно с вероятностью q = 1 - р);
∙при многократном (m-кратном) повторении этого эксперимента ве-
роятность р осуществления события А остается одной и той же, а наблюдения, составляющие эту последовательность экспериментов, являются взаимно независимыми.
Серию экспериментов подобного типа принято называть после-
довательностью испытаний Бернулли.
Можно описать эту последовательность в терминах случайных величин, сопоставляя с i-м по счету экспериментом данной последовательности случайную величину
ξi |
= 1, |
если событие А произошло; |
(1) |
|
0, |
если событие А не произошло. |
|
Тогда «бернуллиевость» последовательности X1, X2, …, |
Xm означает, что |
||
P{X1 = l}= P{X2 = l} =...= P{Xm = l} = p, причем случайные величины X1, X2, …, Xm статистически независимы.
При определенных (как правило, приблизительно соблюдающихся на практике) условиях в схему испытаний Бернулли хорошо укладываются такие случайные эксперименты, как
бросание монеты или игральной кости,
проверка (по альтернативному признаку) изделий массовой продукции,
обращение к «обслуживающему устройству» (с исходами «свободен
–занят»),
попытка выполнения некоторого задания (с исходами «выполнено— не выполнено»),
стрельба по цели (с исходами «попадание – промах») и т. п.
«Единичное» испытание Бернулли можно интерпретировать и как извлечение объекта из бесконечной генеральной совокупности, в которой доля р объектов обладает некоторым интересующим нас свойством.
Тогда интересующее нас событие А заключается в том, что при этом извлечении мы «вытащим» один из объектов, обладающих упомянутым свойством.
Биномиальный закон описывает распределение случайной величины Np(m) = X1 + X2 +…+ Xm, т.е. числа появления интересующего нас события в последовательности из т независимых испытаний, когда вероятность появления этого события в одном испытании равна р.
Из определения биномиальной случайной величины следует, что ее возможными значениями являются все целые неотрицательные числа от нуля до m.
Для вывода вероятностей P{vp (m)= x } (x = 0, 1, 2, т) рассмотрим внимательнее пространство элементарных событий, порожденное последовательностью испытаний Бернулли.
Очевидно, каждому элементарному событию ω соответствует последовательность из нулей и единиц длины т
D1(ω), D2(ω),…, Dm(ω) |
(2) |
Разобьем эти последовательности на классы, включая в один (x-ый) класс все последовательности типа (2), содержащие одинаковое число х единиц:
х = 0: (0, 0,…, 0, 0) = ω(0)

|
(1, 0,..., 0, 0) =ω1 (1) |
||
|
|
|
|
|
(0, 1,..., 0, 0) =ω2 (1) |
||
х = 1: |
............................. |
||
|
|
|
|
|
(0, 0,..., 0, 1) =ω |
m |
(1) |
|
|
|
|
………………………………….. |
|
|
|
|
(1, 1, 1,..., 1, 0,..., 0, 0) = ω1 (k ) |
||
|
|
|
|
|
(0, 1, 1,..., 1, 1,..., 0, 0) = ω2 (k ) |
||
х = k: |
............................. |
|
|
|
|
|
|
|
|
|
|
|
(0, 0, 0,..., 0, 0,..., 1, 1) = ωN ( x) (k ) |
||
………………………………….. |
|
|
|
k = m: (1, 1,…,1,…,1, 1) = |
|
ω(m) |
|
Имея в виду, что число N(x) элементарных событий в классе с номером х равно Сmx (поскольку х единиц можно разместить на т местах Сmx различными способами), а также тот факт, что вероятность осуществления любого элементарного исхода, входящего в класс с номером х, равна, как
нетрудно подсчитать, величине рх(1 – |
р)т- х, получаем |
||
|
|
|
Cmx |
P{vp (m)= x } = P{ω1(x) + ω2(x) +…+ |
ω |
x ( х) } = ∑ p x (1 − p)m −x = |
|
|
Сm |
1 |
|
|
|
|
|
= Сmx рх(1 – р)т- х |
|
|
(3) |
Это и есть формула (аналитическая запись, модель) биномиального закона распределения. Подсчет его основных числовых характеристик (который в данном случае легче реализовать, не используя прямые формулы, а опираясь на соотношение X1 + X2 +…+ Xm, взаимную независимость Xi и простоту вычисления их моментов) дает:
среднее Evp(т) = тр;
мода xmod p(m + 1) – 1 § xmod § p(m +1);
дисперсия Dvp(т) = mp(1 – p);
1 − 2 p
асимметрия B1 = 
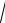 mp(1 − p) ;
mp(1 − p) ;
1 − 6 p(1 − p)
эксцесс B2 |
= |
|
|
. |
|
mp(1 |
− p) |
||||
|
|
|
Биномиальное распределение широко, используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях практической деятельности.
Отрицательный биномиальный закон описывает распределение
случайной величины v_ (k) , |
определяемой испытаниями Бернулли X1, X2, … |
||
p |
|
|
|
|
ν_ ( k )−1 |
|
ν _ ( k ) |
|
p |
|
p |
(1) следующим образом: |
∑ξi |
= k −1 , |
∑ξi = k . |
|
i=1 |
|
i =1 |
Другими словами, v_ (k) |
– это число испытаний в схеме Бернулли (с |
||
p |
|
|
|
вероятностью р появления интересующего нас события в результате проведения одного испытания) до k-го появления интересующего нас события (включая последнее испытание).
Нетрудно вывести аналитический вид распределения случайной
величины v_ (k) .
p
Зафиксируем любое ее возможное значение х. Из того, что при числе
испытаний v_ (k) = x впервые осуществилось заданное число k появлений
p
интересующего нас события, следует, что на предыдущем шаге, т. е. при числе испытаний, равном x – 1, мы имели k – 1 появлений того же события.
Следовательно, опираясь на теорему умножения вероятностей, мы можем записать:
P { v_ |
(k) = x }= [ C k −1 pk −1 |
(1 - p)( x−1)−(k −1) |
] × p |
= |
C k −1 pk (1 − p)x−k , x = k , k + 1 , . . . ( 4 ) |
p |
x−1 |
|
|
|
x−1 |
|
|
|
|
|
Название данного закона объясняется тем, что правые части (4)
являются |
последовательными |
членами |
разложения |
бинома |
с |
||
отрицательным показателем: p k (1 |
– (1 – p )) - k . |
|
|
|
|||
Основные числовые характеристики закона: |
|
|
|
||||
среднее |
E v_ (k) = |
k |
; |
|
|
|
|
|
|
|
|
|
|||
|
p |
p |
|
|
|
|
|
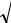
дисперсия D v_ (k) = |
|
k (1 − p) |
; |
|
|||||
|
p2 |
||||||||
|
|
|
p |
|
|
|
|
||
асимметрия B1 = |
|
2 − p |
|
; |
|
||||
|
|
|
|
||||||
|
|
|
|
||||||
k (1− p) |
|||||||||
|
|
1 + 4(1 − p) + (1 − p)2 |
|||||||
эксцесс B2 |
= |
|
|
|
|
|
|
. |
|
|
|
k(1 − p) |
|
||||||
|
|
|
|
|
|
|
|||
Модель отрицательного биномиального распределения применяется:
∙в статистике несчастных случаев и заболеваний,
∙в задачах, связанных с анализом количеств индивидуумов данного вида в выборках из биологических совокупностей,
∙в задачах оптимального резервирования элементов,
∙в теории стрельбы.
2. Гипергеометрическое распределение.
В одном из вариантов интерпретации биномиальной случайной величины vp(т) рассматривается бесконечная генеральная совокупность, доля р объектов которой обладает некоторым интересующим нас свойством. В этом случае vp(т) означает число объектов, обладающих этим свойством среди т объектов, случайно извлеченных из данной генеральной совокупности.
Гипергеометрическую случайную величину vMN(т) можно считать модификацией биномиальной случайной величины vp(т), приспособленной к случаю конечной генеральной совокупности, состоящей из N объектов, среди которых имеются М объектов с интересующим нас свойством.
Иначе говоря, vMN(т) – это число объектов, обладающих заданным свойством среди т объектов, случайно извлеченных (без возвращения) из совокупности N объектов, М из которых обладают этим свойством.
Очевидно, возможными значениями случайной величины vMN(т) будут все целые неотрицательные числа от mах{0, т – ( N – М)} до min{m, M}.
Для вывода аналитического вида ее закона распределения подсчитаем
вероятность события {vMN(т)= х} как отношение числа всевозможных выборок объема m, приводящих к осуществлению этого события (числа

«благоприятных» исходов), к общему числу способов, которыми можно выбрать т объектов из N (к числу всех возможных исходов).
Очевидно, каждому набору из х объектов с заданным свойством соответствует СNm−−Mx способов, которыми можно отобрать остальные т – x объектов из числа объектов, не обладающих этим свойством.
Поскольку такие наборы из х объектов с заданным свойством можно сформировать Сmx различными способами, то общее число
«благоприятных» (для события {vMN(т)= х}) исходов будет Сmx · СNm−−Mx .
Учитывая, что число всех возможных исходов, т. е. всех возможных способов, которыми можно извлечь т объектов из N предложенных, равно
СNm получаем
P{vMN(т)= х} = |
(5) |
x |
m− x |
Cm ×CN − M
CNm
Этот закон широко используется в практике статистического приемочного контроля качества промышленной продукции, а также в различных задачах, связанных с организацией выборочных обследований.
Его основные числовые характеристики:
среднее EvMN(т) = m |
M |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дисперсия DvMN(т)= |
|
|
|
|
M |
|
− |
M |
− |
m |
|
||||||||||||||||||
|
m |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
; |
||||||||||||||
N |
−1 |
|
|
|
|
N |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|||||||||||||||||
|
|
|
1- 2 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
× (N - 2m) N -1 |
||||||||||||||||||||
|
|
|
N |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
асимметрия B1 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N - 2) |
|
|
|
; |
|||||
|
|
M |
|
|
|
|
M |
|
|
|
N - m |
||||||||||||||||||
|
|
m |
|
|
|
|
1- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
N |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
c1(N ) - c2 (N ) × 6 |
M |
- |
M |
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
N |
+ c (N ) + c (N ) |
|
||||
эксцесс B2 = |
|
M |
|
M |
|
|
, где |
|||||||||||
|
|
|
3 |
4 |
||||||||||||||
|
|
|
|
|
|
|
1 - |
|
|
|
|
|
|
|||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
N |
|
N |
|
|
|
|
|
|
||||
c1 |
(N ) = |
|
(N −1)N (N +1) |
; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(N |
- 2)(N |
- 3)(N - m) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c2 (N ) = |
(N -1)N 2 |
; |
|
|
|||
(N - 2)(N - 3)(N - m) |
|||
|
|
|
|
|
|
(N -1)N 2 |
|
|
|
|
|
|
|
|
||||||
|
c3 |
(N ) = 3 |
|
|
|
|
|
-1 ; |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
(N - 2)(N |
- 3)(N - m) |
|
|
|
|
|
|
|
|
||||||
c4 |
(N ) = |
18(N −1) |
|
- |
|
6(N −1) |
|
|
|
|
- |
3(N −1)Nm |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
M |
|
M |
(N - 2)(N - 3)(N - m) . |
||||||||
|
|
|
(N - 2)(N - 3) |
|
(N - 2)(N - |
|
- |
|
||||||||||
|
|
|
|
|
|
|
|
3)m |
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
N |
|
N |
|
|
|
||
При N ض правая часть (5) стремится, к выражению для биномиального закона распределения (3), и соответственно среднее значение, дисперсия, асимметрия и эксцесс гипергеометрического распределения сходятся к аналогичным числовым характеристикам биномиально распределенной случайной величины (что легко устанавливается с помощью соответствующего предельного перехода).
3. Распределение Пуассона.
Если нас интересует число наступлений определенного случайного события за единицу времени, когда факт наступления этого события в данном эксперименте не зависит от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, и не влияет на будущее, а испытания производятся в стационарных условиях, то для описания распределения такой случайной величины обычно используют закон Пуассона (данное распределение впервые предложено и опубликовано этим ученым в 1837 г.).
Этот закон можно также описывать как предельный случай биномиального распределения, когда вероятность р осуществления интересующего нас события в единичном эксперименте очень мала, но число экспериментов m, производимых в единицу времени, достаточно велико, а именно такое, что в процессе р Ø 0 и m Ø ¶ произведение тр стремится к некоторой положительной постоянной величине L (т. е. трØL).
Поэтому закон Пуассона часто называют также законом редких событий.
Обозначим пуассоновскую случайную величину v0(¶) или просто v0 (имея в виду предельный переход от биномиальной случайной величины vp(т) по р Ø 0 и m Ø ¶) и выведем ее закон распределения:
|
|
|
|
|
|
|
|
|
|
lim |
|
P{v |
|
|
(m) = x} = lim C x p x (1 − p)m−x |
|
||||||||||||||||||||||||||||
P { v0 = x } = p→0, m→∞ |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
= |
|
||||||||||||||
|
|
|
|
|
|
|
( pm→λ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
m(m -1)...(m - x +1) |
× |
|
λx |
|
× |
|
- |
λ m−x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x! |
|
|
|
|
|
|
|
m |
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
λx |
|
|
|
λ m |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
x -1 |
|
|
|
λ |
−x |
|
|||||||||||||||||
= |
lim |
x! |
1 |
- |
|
|
|
× |
1 |
- |
|
|
|
× 1 - |
|
|
|
... 1 |
- |
|
|
|
1 |
- |
|
|
|
|
= |
|
||||||||||||||
|
|
|
m |
|
|
|
|
m |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
m |
|
|
|
m |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
x |
|
|
|
λ |
m |
|
|
1 |
|
|
|
|
2 |
|
|
|
x -1 |
|
|
λ |
−x |
|
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= λ × e−λ (x = 0, 1, 2, |
|||||||||||||||||||||||||
= |
|
lim 1 - |
|
|
|
|
|
× lim 1 |
- |
|
|
|
|
1 |
- |
|
|
|
|
... 1 |
- |
|
|
1 |
- |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
x! m→∞ |
|
|
m |
|
m→∞ |
|
m |
|
|
|
|
m |
|
|
|
m |
|
|
m |
|
x! |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
…). (6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда видно, что закон распределения Пуассона зависит от единственного параметра L, содержательно интерпретируемого как среднее число осуществления интересующего нас события в единицу времени.
С помощью «прямого счета» можно подсчитать основные числовые характеристики пуасcоновской случайной величины:
среднее Ev0 = L;
дисперсия Dv0= L;
1
асимметрия B1 = 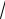 λ ;
λ ;

1
эксцесс B2 = λ .
Пуассоновская случайная величина используется для:
∙описания числа сбоев автоматической линии или числа отказов сложной системы (работающих в «нормальном» режиме) в единицу времени;
∙числа «требований на обслуживание», поступивших в единицу времени в систему массового обслуживания;
∙статистических закономерностей несчастных случаев и редких заболеваний.
Привлекательные прикладные свойства этого закона не исчерпываются вычислительными удобствами и лаконичностью формулы (6) (модель зависит всего от одного числового параметра L!).
Оказывается, эта модель остается работоспособной и в ситуациях, отклоняющихся от вышеописанной схемы ее формирования.
Например, можно допустить, что разные бернуллиевские испытания имеют разные вероятности осуществления интересующего нас события
р1, р2, ..., рп.
В этом случае биномиальный закон применительно к такой серии испытаний уже не может быть применен, в то время как выражение (6) остается приблизительно справедливым и дает достаточно точное описание распределения интересующей нас случайной величины, если только в него
__ __
вместо L = п·р подставить величину L = п· p , где p = (р1 +… + рп)/n.
Сказанное означает, что можно предположить, что анализируемая совокупность состоит из смеси множества разнородных подсовокупностей, таких, что при переходе из одной подсовокупности в другую меняется доля р содержащихся в них объектов с заданным свойством, а следовательно, меняется и среднее число L осуществления интересующего нас события в единицу времени.
Можно далее показать, что если вместо использования среднего значения этих р (или L) (при котором мы остаемся в рамках модели (6)) ввести в рассмотрение закон распределения меняющегося параметра L, интерпретируемого как случайная величина, то мы придем к другому, но в определенном смысле близкому к пуассоновскому закону распределения.
