lab_em1112b / (№2-09)

Лабораторная работа № 2-09

ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ЗАРЯЖЕННЫХ

МЕТАЛЛИЧЕСКИХ СФЕР

Ю.А.Рахштадт

Цель работы

Измерить электрический потенциал и напряженность электростатического поля заряженной металлической сферы.

Теоретическое введение

Закон Кулона. В природе существуют объекты, обладающие электрическим

зарядом. Пространство вокруг электрического заряда q изменяет свои свойства таким образом, что если поместить в него другой электрический заряд qпр (называемый

пробным), то на qпр будет действовать сила F . Говорят, что вокруг неподвижного электрического заряда q существует силовое электрическое поле.

Когда рассматривают электрические силы F на расстояниях r от заряженных тел

размерами L<< r, то в таких ситуациях заряженные тела называют точечными зарядами.

Для величины силы взаимодействия F между двумя точечными зарядами,

находящимися в однородной среде, французским физиком Шарлем Кулоном была

найдена эмпирическая формула:

соединяющей эти заряды, причем одноимённые заряды отталкиваются, а разноименные -

притягиваются друг к другу; r – расстояние между зарядами; ε - относительная диэлектрическая проницаемость однородной среды, зависящая от свойств среды (в

вакууме ε =1); k – коэффициент, зависящий от выбора системы единиц измерения физических величин (например, в системе СГСЭ k = 1, а в СИ k = 1/(4 πε0 ), где ε0 = 8,85· 10-12 Ф/м - электрическая постоянная). В СИ электрические заряды измеряют в кулонах

(Кл).

Формулу (9.1) называют законом Кулона. Действие электрических сил F на точечные заряды показано на рис.9.1.

2

r

Рис.9.1. Действие электрических сил F на точечные электрические заряды q и qпр.

Электрическое поле, возникающее вокруг неподвижных зарядов, называют

электростатическим полем. Электрические силы F в электростатическом поле явно не зависят от времени, но зависят от положения точки в пространстве. Положение точки в

пространстве можно определить, например, радиус-вектором r или декартовыми координатами (x,y,z).

Напряженность E и напряжение U электростатического поля. Электрическое поле вокруг заряда q в точке, определяемой радиус-вектором r , характеризуют величиной

E , называемой напряженностью электрического поля. Чтобы получить значение напряженности E в точке r , в эту точку помещают точечный положительный пробный заряд qпр и измеряют силу F , которая действует на qпр. Напряженность E определяется

формулой:

Напряженность электрического поля является вектором. В СИ величину напряженности Е измеряют в В/м.

Пусть заряд q, создающий электрическое поле, является точечным. Совместим начало радиус-вектора r с положением в пространстве заряда q. Тогда, определив по формуле (9.1) величину силы F, действующую на пробный заряд qпр, с помощью формулы

3

(9.2) получим выражение для величины напряженности Е(r) электростатического поля на расстоянии r от точечного заряда q:

электрического поля, созданного этими зарядами в некоторой точке пространства,

вычисляется по формуле:

Сложение в формуле (9.4) выполняется по правилу сложения векторов. Соотношение (9.4)

часто называют принципом суперпозиции для электрических полей.

Поскольку на заряд q в электрическом поле действует сила F , то, если заряд не

закреплен, он будет перемещаться. При перемещении заряда q из точки 1 в точку 2

электрическое поле совершит работу A12:

Интеграл в правой части равенства (9.5) вычисляется по траектории движения

заряда Под знаком интеграла стоит скалярное произведение векторов и R причем q . F dr ,

конец радиус вектора скользит по траектории движения а вектор R являясь

- , dr , r

бесконечно малым перемещением заряда q вдоль траектории, направлен в каждой точке r

по касательной к траектории. В качестве пределов интегрирования необходимо подставлять координаты начальной точки 1 и конечной точки 2 положения заряда q.

Электростатическое поле обладает следующей особенностью: работа электрических сил A12 по перемещению заряда q в электростатическом поле зависит только от положения начальной точки 1 и конечной точки 2 и не зависит от формы возможных траекторий, соединяющих точки 1 и 2. Такое поле называют потенциальным.

Поэтому, если каждый раз использовать один и тот же точечный заряд q = qпр, величина работы A12по перемещению пробного заряда qпр может служить характеристикой данного электрического поля.

Отношение работы A12 к величине точечного положительного заряда qпр

называют разностью потенциалов ϕ1 − ϕ2 точек 1 и 2 в данном электростатическом поле.

Разность потенциалов электростатического поля называют ещё электрическим напряжением U12 между точками 1 и 2. Таким образом:

4

Разность потенциалов или электрическое напряжение (также как и работа A12)

является скалярной величиной. В СИ разность потенциалов ϕ1 − ϕ2 и электрическое напряжение U12 измеряется в вольтах (В).

Найдем связь между напряжением U и напряженностью E электростатического

поля. На основании формул (9.2), (9.5) и (9.6) можно записать:

A12 = qпр(ϕ1 − ϕ2 ) = qпрU12.

Приравнивая правые части последних равенств друг к другу и сокращая на qпр ,

получаем искомую связь:

Потенциал ϕ электростатического поля. Если в качестве точки 2 брать одну и ту

же точку (как начало координат), а под точкой 1 понимать любую точку электрического поля, то для краткости можно говорить об электрическом потенциале ϕ точки 1, хотя при этом подразумевается разность потенциалов между произвольной точкой электрического поля и некоторой фиксированной точкой 2. Часто (но не всегда) в качестве фиксированной точки 2 берут точку на бесконечности, т.е. очень далеко от системы зарядов, которые создают электрическое поле.

Итак, потенциалом ϕ электростатического поля в некоторой точке называют

ϕ2 = 0 . В частности, если точка 2 выбрана на бесконечности, то ϕ2 = ϕ∞ = 0 .

Выбирая в (9.7) в качестве нижнего предела интегрирования координату

5

Из формул (9.8) и (9.3) следует, что потенциал ϕ(r ) электростатического поля на расстоянии r от точечного заряда q равен:

потенциала ϕ . Градиент ϕ направлен в сторону наибыстрейшего возрастания потенциала

ϕ в пространстве.

i =1

где ϕi - потенциал электрического поля, созданного зарядом qi в данной точке. Сложение величин ϕi в формуле (9.11) выполняется с учетом знаков потенциалов поля отдельных зарядов. Соотношение (9.11) называют принципом суперпозиции для потенциалов электрического поля.

Теорема Гаусса. Когда заряженное тело не может считаться точечным зарядом, то процедура вычисления E в общем случае усложняется. Упрощения возможны в так называемых симметричных случаях. Для симметричных равномерно заряженных тел конечных или бесконечных размеров процесс определения напряженности электростатического поля можно упростить с помощью теоремы Гаусса: поток ФЕ вектора напряженности электрического поля через произвольную замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постояннуюε0 (в СИ) и диэлектрическую проницаемость среды ε :

данной точке.

6

Отметим, что наличие или отсутствие электрических зарядов, находящихся вне выбранной поверхности S, никак не влияет на справедливость равенства (9.12).

Поверхность S часто называют гауссовой поверхностью.

Напряженность E и потенциал ϕ электростатического поля внутри и вне

равномерно заряженной сферической поверхности. Пусть на равномерно заряженной сферической поверхности радиуса R находится суммарный электрический заряд q, среда внутри и вне сферы имеет относительную диэлектрическую проницаемость ε. Требуется найти напряженность электростатического поля во всем пространстве.

Поскольку задача обладает сферической симметрией, применим теорему Гаусса.

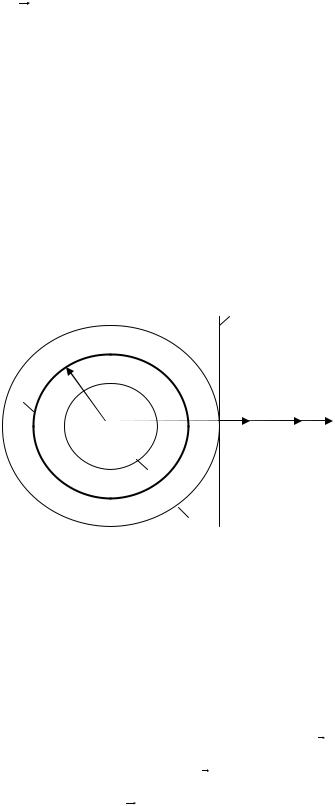
Начало координат 0 возьмем в центре сферы, а координатную ось r проведём вдоль одного из радиусов сферы в произвольном направлении (рис.9.2). Из соображений

S1

Рис.9.2. Применение теоремы Гаусса к расчету напряженности E(r)

электростатического поля внутри и вне равномерно заряженной сферы.

а) Поле вне сферы: r = r1 ³ R .

Через точку r1 на координатной оси r проведём воображаемую поверхность Гаусса

S1 в виде сферы радиусом r1 с центром в точке 0 (см. рис.9.2). В точке r1 к сфере S1

проведём касательную плоскость Р и построим единичный вектор n , перпендикулярный

Р. Из геометрии известно, что вектор нормали n в этой точке направлен по оси r.

Очевидно, что вектор напряженности E(r) электрического поля также будет направлен вдоль оси r. Записываем теорему Гаусса:

Проводя через точку r2 воображаемую поверхность Гаусса S2 в виде сферы радиуса r2 с центром в точке 0 (см. рис.9.2), рассуждая аналогичным образом (как и выше в п. а)) и

замечая, что внутри поверхности S2 суммарный электрический заряд равен нулю, можно

прийти к равенству:

Формулы (9.13) и (9.14) можно объединить в одну:

Используя формулу (9.15) для вычисления интеграла в правой части равенства (9.8)

с учетом геометрии, изображенной на рис. 9.2, получим формулу для расчета потенциала

8

На рис.9.3 представлены графики распределения модуля вектора напряженности и потенциала электрического поля внутри и вне заряженной сферы, отвечающие зависимостям этих величин от расстояния до центра сферы согласно формулам (9.15) и

(9.16).

а) 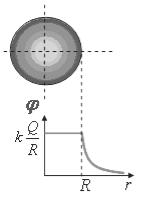б)

Рис.9.3. Зависимость модуля вектора напряженности (а) и потенциала (б) электрического поля металлической сферы от расстояния до центра сферы.

В воздухе (ε = 1) вне равномерно заряженной сферы радиуса R с общим зарядом q

на расстоянии a от ее поверхности потенциал ϕ и напряженность Е электрического поля,

как это следует из формул (9.15), (9.16), описываются соотношениями

где коэффициент пропорциональности С называют электрической емкостью проводника.

Это позволяет выразить заряд q на сфере через электрическую емкость сферы

C = 4πε0 R и потенциал на поверхности сферы ϕ(R):

10

работу измерительной системы. Горелка должна быть отрегулирована таким образом,

чтобы пламя располагалось примерно на 5 мм выше заостренного конца зонда 4.

Сфера 1, зонд 4 и горелка 8 установлены на штативах, которые могут перемещаться вдоль линейки 10. Положения сферы 1 и зонда 4 определяются на линейке по левым

краям оснований штативов (см. рис.9.4) – для сферы х0 , для зонда хi .

Технические данные приборов внесите в таблицу 9.1.

Таблица 9.1. Технические характеристики приборов.

Порядок выполнения работы

При выполнении работы необходимо строго соблюдать требования по технике безопасности и охране труда, установленные на рабочем месте студента в лаборатории.

Внимание! Все оборудование должно быть заземлено!

На металлической сфере 1 может быть высокое напряжение до 10 кВ. До сферы не дотрагиваться! Человеческое тело сильно влияет на электростатическое поле в воздухе.

Поэтому во время измерений нужно находиться подальше от сферы 1 и зонда 4, а

вольтметр 7 должен лежать у правого края лабораторного стола.

1.Попросите лаборанта перед началом работы снять электрический заряд со сферы.

2.Проверьте, чтобы левый край основания штатива, на котором закреплена сфера 1,

совпадал с нулевой отметкой на линейке 10 (x0 = 0). Поставьте левый край основания штатива, на котором закреплен зонд 4 с горелкой 5, на отметку

х1 = 460мм на линейке. Убедитесь, что зонд находится на одной высоте с центром сферы. Не касаясь рукой сферы, измерьте наименьшее расстояние a1 между поверхностью сферы и заостренным концом зонда (a1≈50 мм). Значение a1

запишите в таблицу 9.2.

3.Попросите лаборанта подать напряжение на ИЭП и включить на нем режим

100кВ/м. На вольтметре 7 включить диапазон (0-10)В и с помощью ручки на ИЭП