Тема 5 Предельные теоремы теории вероятностей

Теорема «закона больших чисел», Центральная предельная теорема. Интегральная теорема Лапласа как частный вид центральной предельной теоремы.

Практическое занятие включает рассмотрение примеров на использование теорем Чебышева и Бернулли, а также интегральной теоремы Лапласа.

Вопросы

1. В чем состоит свойство устойчивости массовых случайных явлений?

2. Дайте общую характеристику закона больших чисел и центральной предельной теоремы как фундаментальных составляющих совокупности предельных теорем теории вероятностей.

3. Изложите содержание теоремы Чебышева и теоремы Бернулли.

4. Дайте формулировку центральной предельной теоремы (теоремы Ляпунова).

5. Почему интегральную теорему Лапласа можно считать частным видом центральной предельной теоремы?

6. Изложите содержание интегральной теоремы Лапласа.

Примеры

Пример 1. При каком числе называемых испытаний вероятность выполнения неравенства превысит, если вероятность появления события в отдельном испытании?

Решение. По условию задачи ,, поэтому; требуется определитьс помощью неравенства теоремы Бернулли

.

Условие равносильно неравенству, откудапри подстановке значений,ив последнее неравенство находим.

Следовательно, требуемое неравенство выполняется при числе независимых испытаний, начиная с 132.

Пример 2. Известно, что дисперсия каждой из последовательности независимых случайных величин не превышает 4. Определить число таких величин, при котором вероятность отклонения средней арифметической случайной величины от средней арифметической их математических ожиданий не более чем на превысит.

Решение. Неравенство теоремы Чебышева

где - независимые случайные величины, имеющие конечные математические ожиданияи дисперсии, ограниченные одним и тем же числом;- любое положительное число, приипринимает вид

.

Из условия следует, что , откуда, или.

Итак, .

Пример 3. Дана последовательность независимых случайных величин каждаяиз которых может принимать значения:,0,соответственно с вероятностями,,. Можно ли к этим величинам применить теорему Чебышева?

Решение. Чтобы дать ответ на поставленный вопрос, необходимо проверить ограниченность дисперсий данных случайных величин одной и той же постоянной С (остальные условия теоремы Чебышева выполняются: независимость случайных величин и достаточно большое их число).

Для этого сначала найдем их математические ожидания:

.

Математические ожидания их квадратов:

.

Так как , то дисперсии всех случайных величинодинаковы, они ограничены одним числом. Следовательно, к данным случайным величинам можно применить теорему Чебышева.

Пример 4. Вероятность появления положительного результата в каждом из опытов равна. Сколько опытов нужно провести, чтобы с вероятностьюможно было ожидать, что не менее 150 опытов дадут положительный результат?

Решение. Воспользуемся формулой интегральной теоремы Лапласа

.

В соответствии с условием задачи ,,,(значениенужно определить) данная формула принимает вид, или

Очевидно, что , поэтому. Поскольку функция Лапласа – возрастающая и, то можно положить.

Следовательно, ,.

По таблице значений приведенной функции Лапласа находим . Тогда, учитывая нечетность функции Лапласа, получаем.

Решая это уравнение, как квадратное относительно , находим,.

Задачи

1. Вероятность положительного исхода отдельного испытания . Оценить вероятность того, что при 1000 независимых испытаний отклонение частоты положительных исходов от вероятности при отдельном испытании по модулю будет меньше 0,05.

2. Сколько следует провести независимых испытаний, чтобы вероятность выполнения неравенства превысила 0,78, если вероятность появления данного события в отдельном испытании?

3. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно провести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие А появится не менее 75 раз?

4. Производство дает 1% брака . Найти вероятность того, что из взятых на исследование 1100 изделий бракованных будет не более 17.

Тема 6

Распределение функции случайного аргумента.

Закон распределения монотонной функции одного случайного аргумента

Практическое занятие включает:

- определение закона распределения функции случайного аргумента;

- определение плотности распределения монотонной функции одного случайного аргумента.

Вопросы

1. Понятие функции одного случайного аргумента.

2. Запишите формулу плотности распределения монотонной функции одного случайного аргумента.

Примеры

Пример 1. Дискретная случайная величина задана законом распределения :

	1	3	5
	0,4	0,1	0,5

Найти закон распределения случайной величины .

Решение. Найдем возможные значения величины . Имеем:;;. Для того, чтобыдостаточно, чтобы величинаприняла значения. Но вероятность событияпо условию равна 0,4; следовательно и вероятность событиятакже равна 0,4.

Аналогично получим вероятности остальных возможных значений :

;

.

Тогда искомый закон распределения :

	3	9	15
	0,4	0,1	0,5

Пример 2. Дискретная случайная величина задана законом распределения

	-2	-1	0	1	2
	0,1	0,2	0,15	0,25	0,3

Найти закон распределения и МО случайной величины .

Решение. - новая СВ, которая с теми же вероятностями, что и СВ, принимает значения, равные квадратам ее значений.

Квадраты СВ равны: 4, 1, 0, 1, 4, т.е. величинапринимает значения,,.

Закон распределения СВ можно записать в виде:

	0	1	4
	0,15	0,45	0,4

Вероятность 0,45 для значения получена по теореме сложения вероятностей, с которыми СВпринимает значения,. Аналогично получена вероятность 0,4 для значения.

Согласно формуле находим МО функции:

.

Пример 3. Дискретные независимые случайные величины заданы законами распределения:

	5	6			7	8
	0,4	0,6			0,8	0,2

Составить закон распределения случайной величины .

Решение. Возможные значения величины есть суммы каждого возможного значениясо всеми возможными значениями:

, ,,.

Найдем вероятности этих возможных значений. Для того чтобы , достаточно, чтобы величинаприняла значениеи величина- значение. Вероятности этих возможных значений соответственно равны 0,4 и 0,8. Величиныинезависимы; следовательно, вероятность их совместного появления (т.е. вероятность события) по теореме умножения равна.

Аналогично находим:

,

,

.

Величина принимает три разных значения 12, 13, 14. Поскольку события () и () несовместны, то

.

Таким образом величина имеет закон распределения

	12	13	14
	0,32	0,56	0,12

Отметим, что 0,32+0,56+0,12=1, как и должно быть.

Пример 4. Дискретная случайная величина имеет закон распределения.

	0	1	2	3
	0,1	0,3	0,4	0,2

Найти закон распределения СВ .

Решение. Найдем значение функции .

При получаем соответственно числа. Следовательно, возможными значениями случайной величиныявляются числа,,.

Вероятности этих значений:

; ;

.

Таким образом, закон распределения СВ имеет вид:

	0	1	2
	0,2	0,5	0,3

Пример 5. Случайная величина задана плотностью распределения

Найти плотность распределения функции .

Решение. На отрезке возможных значений случайной величины функция- монотонно возрастающая. Обратная ей функциятакже монотонно возрастает на отрезке [1; 4] – области возможных значений случайной величины. Находим производную обратной функции

.

Применяя формулу , находим

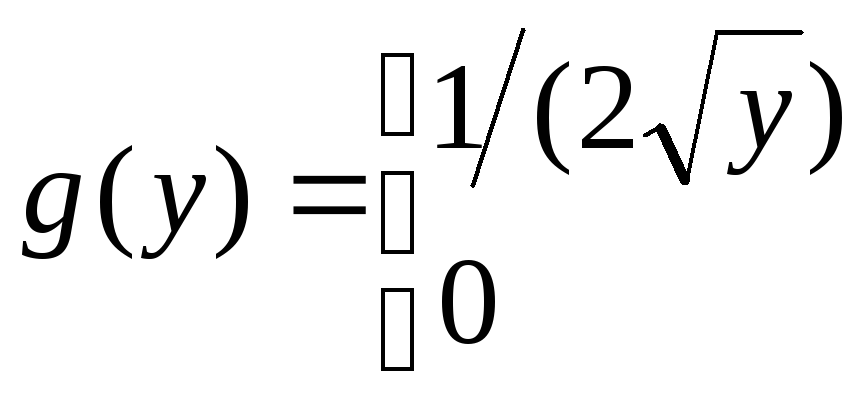
Пример 6. Случайная величина задана плотностью распределения

Найти плотность распределения .

Решение. Поскольку функция является дифференцируемой и строго монотонной, то можно применить формулу для, использованную в предыдущем примере.

Найдем функцию , обратную функции:.

Тогда (1)

Производная обратной функции из :

(2)

Подставляя выражения (1) и (2) в формулу для определения , получим искомую плотность распределения функции:

.

Пример 7. Непрерывная случайная величина задана плотностью распределенияв интервале (0;), вне этого интервала. Найти математическое ожидание функции.

Решение. Воспользуемся формулой

.

Тогда

Задачи

1. Дискретная случайная величина задана законом распределения.

	-1	-2	1	2
	0,3	0,1	0,2	0,4

Найти , если.

2. Дискретная СВ задана законом распределения

	1	2	3	4	5
	0,1	0,2	0,4	0,2	0,1

Записать закон распределения СВ .

3. Дискретные независимые случайные величины изаданы законами распределения

	-1	-2			5	7
	0,3	0,7			0,6	0,4

Составить закон распределения случайной величины .

4. Дискретная СВ задана законом распределения

	0,2	0,7	0,1

Найти закон распределения СВ

5. Случайная величина распределена равномерно в интервале (0;). Найти плотность распределенияслучайной величины.

6. Непрерывная случайная величина задана плотностью распределенияв интервале (0; 2); вне этого интервала. Найти МО функции.