Примеры

Пример 1. На шести одинаковых карточках написаны буквы слова «талант». Карточки вынимают наудачу одну за другой. Какова вероятность снова получить слово «талант»?

Решение. Мысленно пронумеруем карточки с буквами. Слово «талант» не изменится, если буквы «Т» переставить местами (получаем две комбинации). Если в каждой из этих двух комбинаций то же проделать с буквой «а», то в результате получим 4 различные комбинации. Таким образом, появлению слова «талант» благоприятствует 4 элементарных исхода.

Общее число равновозможных элементарных исходов равно числу перестановок из 6-ти элементов: . Тогда по формуле классического определения вероятности события А (в данном случае состоящего в получении слова «талант»)

, где - число исходов, благоприятствующих этому событию,- число всех равновозможных несовместных элементарных исходов, образующих полную группу,

.

Замечание 1. Искомую вероятность можно найти с помощью формулы числа перестановок с повторениями:

где - элементы первого вида,- элемент второго вида, …,- элементы-го вида, т.е. .

Тогда =>.

Замечание 2. Ту же вероятность можно найти по теореме умножения вероятностей

.

Пример 2. (Задача де Мере).

Сколько раз нужно подбросить два игральных кубика, чтобы вероятность выпадения хотя бы один раз двух шестерок была бы больше 1/2?

Решение. Пусть событие - выпадение двух шестерок при i - м подбрасывании. Вероятность этого события

,

откуда вероятность противоположного события

.

Подбрасывания игральных кубиков – независимые испытания, поэтому вероятность выпадения хотя бы один раз 2-х шестерок определяется по формуле

,

которая в данном случае принимает вид

или .

Логарифмируя, получаем

,

откуда

.

Таким образом, чтобы вероятность выпадения двух шестерок была больше , необходимо подбросить кубик не менее 25 раз.

Пример 3. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов .

Определяем число исходов, благоприятствующих событию - «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взятьспособами, при этом остальные 6-4=2 детали должны быть нестандартными; взять же две нестандартные детали из 10-7=3 нестандартных деталей можноспособами. Следовательно, число благоприятных исходов равно.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

.

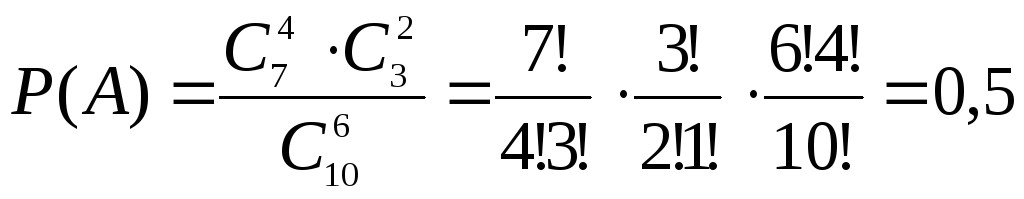Пример 4. На 30 одинаковых жетонах написаны 30 целых чисел от 1 до 30. Жетоны помещены в пакет и тщательно перемешаны. Какова вероятность вынуть жетон с номером, кратным 2 и 3?

Решение. Обозначим события: - «извлечен жетон с четным номером»,- «извлечен жетон с номером, кратным 3»,- «извлечен жетон с четным номером, кратным 3». Найдем вероятность события. Посколькуи- совместные события, то

.

(Событию благоприятствует 15 элементарных исходов, событию- 10 исходов, событию- 5 исходов).

Пример 5. Электрическая цепь между точками иимеет схему, изображенную на рис.

Элемент	1	2	3	4
Вероятность	0,6	0,8	0,7	0,9

Различные элементы цепи работают независимо друг от друга. Вероятности безотказной работы элементов за время приведены в таблице.

Определить вероятность безотказной работы системы за время .

Решение. Участок электрической цепи пропускает ток (событие) в случае совмещения следующих трех событий:- работает элемент 1,- работает элемент 4 и- работает хотя бы один из двух элементов 2 и 3, т.е..

Так как события ,инезависимы, то

.

Для нахождения вычислим вероятность события- заключающегося в том, что элементы 2 и 3 вышли из строя. Посколькуи событияинезависимы, то

.

Отсюда .

Таким образом, .

Пример 6. На складе находятся детали, изготовленные на двух заводах. Известно, что объем продукции первого завода в 4 раза превышает объем продукции второго завода. Вероятность брака на первом заводе , на втором заводе -. Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена первым заводом?

Решение. Обозначим через событие, состоящее в том, что взятая деталь изготовлена на первом заводе,- на втором заводе, тогда

, .

Пусть - событие, состоящее в том, что на удачу взятая деталь оказалась бракованной.

По условию ,.

В соответствии с формулой Байеса

,

где- формула полной вероятности;,,…,- попарно несовместные события (гипотезы),

.

Задачи

1. Из букв слова «ротор», составленного с помощью разрезной азбуки, наудачу последовательно извлекаются три буквы и складываются в ряд. Найти вероятность того, что получится слово «тор».

2. Из букв разрезной азбуки составлено слово «институт». Затем карточки с буквами перемешивают и вновь собирают в произвольном порядке. Найти вероятность того, что снова получится слово «институт».

3. Из колоды карт (36) наудачу вынимаются три карты. Найти вероятность того, что среди них окажется: а) один туз; в) хотя бы один туз.

4. Из колоды карт последовательно вынуты две карты.

Найти: а) безусловную вероятность того, что вторая карта окажется тузом; в) условную вероятность того, что 2-я карта будет тузом, если 1-я также была тузом.

5. В технической системе дублированы наименее надежные узлы.

Надежность (вероятность безотказной работы) каждого из узлов дана на схеме.

Определить

надежность

системы.

6. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго – 0,8. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один спортсмен.

7. На предприятии изготавливаются изделия на трех поточных линиях. На первой линии производится 30% изделии, на второй – 25%, на третьей – остальная часть продукции. Каждая из линий характеризуется соответственно следующими процентами годности: 97%, 98%, 96%. Наугад взятое изделие оказалось бракованным. Определить вероятность того, что это изделие изготовлено на первой линии.