
- •Федеральное агентство по образованию
- •Введение
- •Тема 1 Основные понятия теории вероятностей. Элементы комбинаторики. Теоремы сложения и умножения вероятностей и их следствия
- •Вопросы
- •Примеры
- •Тема 2 Случайные величины и законы их распределения. Закон распределения вероятностей и числовые характеристики дискретной случайной величины. Повторение испытаний
- •Вопросы
- •Примеры
- •Тема 3 Функция распределения вероятностей как универсальная характеристика случайной величины (св). Плотность распределения вероятностей непрерывной св
- •Вопросы
- •Примеры
- •Тема 4 Важнейшие законы распределения непрерывной св
- •Вопросы
- •Примеры
- •Тема 5 Предельные теоремы теории вероятностей
- •Вопросы
- •Примеры
- •Тема 7 Исследование системы двух случайных величин
- •Вопросы
- •Примеры
- •Примеры
- •2. Критерий Романовского
- •Примеры
- •Тема 10 Элементы теории случайных процессов. Характеристики случайных функций (сф)
- •Вопросы
- •Примеры
- •Тема 11 Стационарные случайные функции (ссф)
- •Вопросы
- •Примеры
- •Основные правила дифференцирования
- •Барсуков Владимир Иванович
Тема 10 Элементы теории случайных процессов. Характеристики случайных функций (сф)
Свойства МО, дисперсии, корреляционной функции (КФ). Характеристики суммы случайных функций, производной СФ, интеграла от СФ.
Практическое занятие включает:
- решение задач на определение МО, КФ и дисперсии случайной функции;
- определение характеристик СФ на выходе типовых динамических звеньев.
Вопросы
Понятие случайной функции.
Объясните, что называется реализацией и сечением случайной функции.
Является ли реализация случайной функцией?
Понятие математического ожидания случайной функции.
Перечислите свойства математического ожидания случайной функции.
Перечислите свойства дисперсии случайной функции.
Что называется центрированной случайной функцией?
Дайте определение корреляционной функции случайной функции
 .
.Изложите свойства корреляционной функции.
Понятие нормированной корреляционной функции.
Понятие корреляционной матрицы.
Понятие взаимной корреляционной функции.
Перечислите свойства взаимной корреляционной функции.
Дайте формулировку теоремы о математическом ожидании суммы конечного числа случайных функций.
Дайте формулировку теоремы о корреляционной функции суммы двух корреляционных функций.
Чему равна корреляционная функция суммы некоррелированных случайных функций?
Чему равна корреляционная функция случайной функции и некоррелированной с ней случайной величины?
Объясните понятие сходимости в среднем квадратическом.
Как определяется математическое ожидание производной от случайной функции
 ?
?Чему равна корреляционная функция производной от случайной функции
 ?
?Приведите формулы дл определения взаимной корреляционной функции случайной функции
 и ее производной.
и ее производной.Понятие интеграла от случайной функции.
Чему равно математическое ожидание интеграла от случайной функции?
Как определяется корреляционная функция интеграла от случайной функции?
Примеры
Пример
1. Задана
случайная функция
![]() ,где U
– случайная
величина (М (U)=5,
D
(U)=6).
,где U
– случайная
величина (М (U)=5,
D
(U)=6).
Найти МО, КФ и дисперсию случайной функции Х(t).
Решение.
С учётом свойства математического
ожидания, состоящего в том, что неслучайный
множитель
![]() можно выносить
за знак МО, имеем
можно выносить
за знак МО, имеем
![]() .
.
![]() .
.
По формуле для корреляционной функции (КФ) случайной функции Х(t) получаем

Учитывая, что
![]() ,
,
![]() .
.
Для
определения дисперсии нужно положить
![]() :
:
![]() .
.
Пример
2. Найти
взаимную КФ случайных функций
![]() и
и![]() ,
гдеU
– случайная величина
,
гдеU
– случайная величина
![]() .
.
Решение. Математические ожидания
![]() ,
,
![]() .
.
Центрирование функции
![]() ,
,
![]() .
.
Тогда по формуле для взаимной КФ получаем
![]() .
.
Пример
3. На вход
дифференцирующего звена поступает
случайная функция Х(t)
с математическим ожиданием
![]() и корреляционной функцией
и корреляционной функцией![]() ,
гдеDх
– постоянная дисперсия. Определить
математическое ожидание и дисперсию
на выходе системы.
,
гдеDх
– постоянная дисперсия. Определить
математическое ожидание и дисперсию
на выходе системы.
Решение.
Случайная функция
![]() на выходе системы (реакция) связана с
воздействием
на выходе системы (реакция) связана с
воздействием![]() оператором дифференцирования:
оператором дифференцирования:
![]() .
.
Применяя формулы математического ожидания и корреляционной функции производной от случайной функции Х(t), получаем
![]() ,
,
![]() ,
,

Полагая
![]() ,
имеем
,
имеем
![]() или
или
![]() ,
,
т.е.
дисперсия на выходе дифференцирующего
устройства зависит не только от дисперсии
на входе, но и от коэффициента
![]() ,
характеризующего быстроту затухания
корреляционной связи между сечениями
случайной функции Х(t)
при возрастании промежутка между ними.
,
характеризующего быстроту затухания
корреляционной связи между сечениями
случайной функции Х(t)
при возрастании промежутка между ними.
Если
коэффициент
![]() мал, корреляционная связь затухает
медленно, случайная функция изменяется
во времени сравнительно плавно, и поэтому
дифференцирование такой функции приводит
к сравнительно малым ошибкам.
мал, корреляционная связь затухает
медленно, случайная функция изменяется
во времени сравнительно плавно, и поэтому
дифференцирование такой функции приводит
к сравнительно малым ошибкам.
Если
коэффициент
![]() велик, корреляционная функция убывает
быстро, а, следовательно, в составе
случайной функции преобладают
высокочастотные колебания; дифференцирование
такой функции приводит к большим
случайным ошибкам.
велик, корреляционная функция убывает
быстро, а, следовательно, в составе
случайной функции преобладают
высокочастотные колебания; дифференцирование
такой функции приводит к большим
случайным ошибкам.
Пример
4. Задана
случайная функция
![]() ,
гдеU
– случайная величина (М(U)
= 1, D(U)
=1). Найти: МО, КФ и дисперсию случайной
функции
,
гдеU
– случайная величина (М(U)
= 1, D(U)
=1). Найти: МО, КФ и дисперсию случайной
функции
![]()
Решение.
По формулам для МО и КФ интеграла от
случайной функции
![]()
![]() ,
,

получаем
![]() ;
;
![]()

![]() ,
,
откуда
![]() .
.
Задачи
Найти МО, КФ и дисперсию случайной функции
 ,
гдеU
– случайная величина, причём М(U)=10,
D(U)=0,2.
,
гдеU
– случайная величина, причём М(U)=10,
D(U)=0,2.Найти МО, КФ и дисперсию случайной функции
 ,
гдеU
и V
– некоррелированные случайные величины,
причём М(U)=1,
М(V)=8,
D(U)=D(V)=4.
,
гдеU
и V
– некоррелированные случайные величины,
причём М(U)=1,
М(V)=8,
D(U)=D(V)=4.Задана корреляционная функция
 случайной функцииХ(t).
Найти КФ её производной.
случайной функцииХ(t).
Найти КФ её производной.На вход дифференцирующего звена поступает случайная функция Х(t) с математическим ожиданием
 и корреляционной функцией
и корреляционной функцией .
Найти МО и КФ выходной функции
.
Найти МО и КФ выходной функции .
.Задана случайная функция
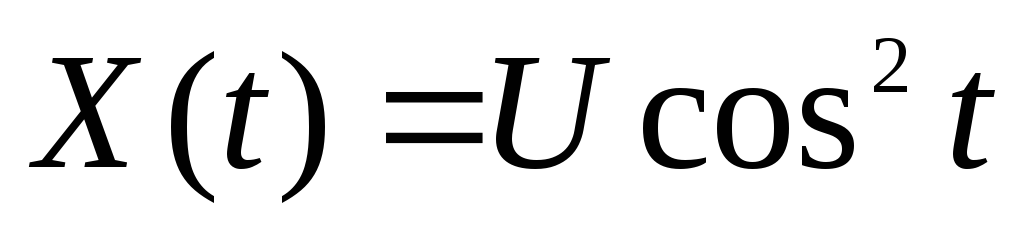 ,
гдеU
- случайная величина, причём М(U)=2.
Найти математическое ожидание случайной
функции
,
гдеU
- случайная величина, причём М(U)=2.
Найти математическое ожидание случайной
функции
 .
.На вход интегрирующего устройства поступает случайная функция Х(t), корреляционная функция которой
 .
Найти дисперсию на выходе интегратора.
.
Найти дисперсию на выходе интегратора.
