
Аналитико-прогнозюю. забезп_управл / Практические / АПЗУ_практ_звіти / АПОУ Практ. Журавлева, Коновалова / Коновалова А. семинар 2
.docКоновалова А. ДИД/м-10
Семінарське заняття № 2
ПРОГНОЗУВАННЯ ОБСЯГУ ВИРОБНИЦТВА ЗА МОДЕЛЛЮ ТЕЙЛА-ВЕЙДЖА
Г. Тейл и С. Вейдж аналогично тому, как это сделал Д. Мат при изучении экспоненциальной средней, в целях дальнейшего изучения свойств адаптивных моделей предложили применить двухпараметрический предиктор Хольта для прогнозирования некоторого вероятностного процесса, характеризующегося стохастическим трендом. Они вывели выражения для определения оптимальных параметров адаптации, минимизирующих средний квадрат ошибки прогнозирования.
Процесс Тейла-Вейджа аналитически записывается как:

где eh, t - значение уровня исследуемого временного ряда xt в момент t;
f - прирост уровня от момента t - 1 к моменту t\
Et, 'vt - временные последовательности с нулевым математическим ожиданием, постоянными дисперсиями и отсутствием ковариации, т. е.

M(ptet') = Q для любой пары (t, t').
Временной ряд xt не является стационарным и не имеет строго определенной автоковариационной функции.,
Однако М. Нерлов и С. Вейдж показали, что из уравнений (1.12) следует стационарность вторых разностей процесса xt) которые мы обозначим через yt:
yt = (Xt-xt^~(xt^~-xt.2)=Vixt^zallt+VHtr=vt+V2et,
где V-разностный оператор, Vxt = xt- xt-i, V2xt.= V(Vxt).
Вторые разности имеют вполне определенную автоковариационную функцию.

Эти свойства могут быть использованы для решения вопроса о возможности адекватного представления наблюденного временного ряда процессом Тейла-Вейджа. При этом не следует упускать из виду то обстоятельство, что оценки автоковариационной функции являются довольно грубыми и коррелированными и точные равенства на практике будут выполняться лишь приближенно.
Схема составления прогноза в соответствии с выглядит следующим образом:
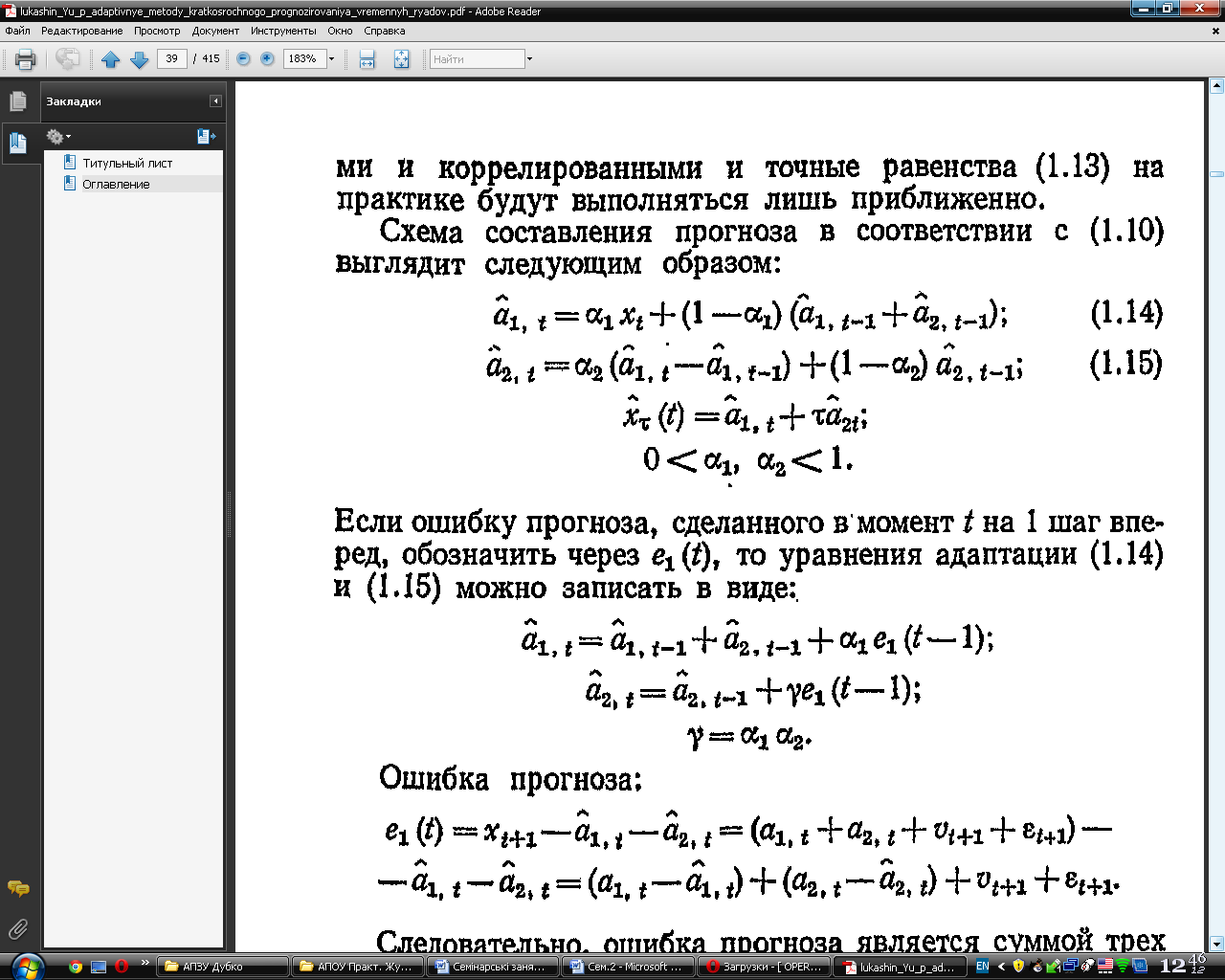
Если ошибку прогноза, сделанного в момент t на 1 шаг вперед, обозначить через e1(t), то уравнения адаптации и можно записать в виде:


Следовательно, ошибка прогноза является суммой трех компонент: ошибки оценки уровня процесса в момент t, ошибки оценки прироста уровня в момент t и комбинации
случайных компонент v и е в момент t + 1.
Очевидно, что определение оптимальных ах и у эквивалентно определению оптимальных ах и а2. Оптимум обычно отыскивается путем минимизации среднего квадрата ошибки прогноза. Но когда рассматриваются нестационарные временные ряды, то в общем случае не очевидно, что средний квадрат ошибок прогнозирования адаптивным методом является величиной устойчивой, которая может быть минимизирована. Используя соотношение
![]()
Нерлов и Вейдж показали, что проблема прогнозирования xi + 1 эквивалентна задаче прогнозирования второй разности yt + 1 и что при ограничениях, наложенных на параметры адаптации с и а2, ошибка прогноза является линейной комбинацией текущего и прошлых значений стационарного ряда уt.
![]()
где {c} - сходящийся ряд весов.
Это означает, что ошибки прогноза стационарны и их средний квадрат вполне определенен. В результате минимизации дисперсии ошибки прогноза на 1 шаг вперед De (1) Тейл и Вейдж получили следующие результаты:

Грубая оценка соотношения дисперсий ga может быть получена из соотношений (1.13) по подсчитанным автоковариациям процесса yt. Уточнение g* производится экспериментально методом проб на имеющемся отрезке ряда. Давая значения в окрестностях грубой оценки, находят ga, минимизирующее дисперсию ошибки De (1).
Нерлов и Вейдж провели теоретический анализ чувствительности дисперсии ошибки прогноза De(l) к ошибкt в определении g2. Оказалось, что процентное изменение дисперсии De (1) пропорционально квадрату относительной ошибки оценки g2 с коэффициентом пропорциональности
![]()
Для наиболее реальных, малых значений g2 даже 50 % -ная ошибка в оценке g2 дает увеличение в De (1) менее чем на 1,5%.
