2.4 Устойчивость систем автоматического регулирования и управления

2.4.1. Понятие об устойчивости системы

Система автоматического регулирования или управления, как любая динамическая система, характеризуется переходным процессом, возникающим в ней при нарушении ее равновесия каким-либо воздействием; это могут быть сигналы управления, настройки, помехи и т. п.

Переходный процесс x(τ) зависит как от свойств системы, так и от вида возмущения. В переходном процессе всегда следует различать две составляющие. Первая составляющая— это свободные движения системы x_c(τ), определяемые начальными условиями и свойствами самой системы; вторая составляющая — вынужденные движения x_B(τ), определяемые возмущающим воздействием и свойствами системы. Таким образом можно написать:

x(τ)=x_с(τ)+x_B(τ). (2.21)

Одной из основных динамических характеристик системы регулирования является ее устойчивость (или неустойчивость). Для выполнения практических задач регулирования система прежде всего должна быть устойчива. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, нарушившего указанное равновесие. Неустойчивая системa не возвращается к состоянию равновесия, из которого она по тем или иным причинам вышла, а непрерывно удаляется от него или совершает около него недопустимо большие колебания. Очевидно, что неустойчивые системы регулирования применяться для работы не могут. Поэтому, для того чтобы система могла правильно реагировать на сигнал управления, настройки или изменения нагрузки, в переходном процессе свободная составляющая с течением времени должна стремиться к нулю, т. е

(2.22)

следовательно, характер свободного движения системы определяет ее устойчивость или неустойчивость.

Аналитическая формулировка условия устойчивости определяется выражением (2.22); при невыполнении условия (2.22) система считается неустойчивой.

В вопросах суждения об устойчивости систем автоматики имеют большое практическое значение общие теоремы устойчивости, сформулированные А.М.Ляпуновым и приводимые ниже без аналитического доказательства. Эти теоремы позволяют установить значение и сферу применения линеаризации нелинейных уравнений, т. е. правомерность отнесения к линейным системам большинства реальных систем. Теоремы формулируются следующим образом:

1. Нелинейная система устойчива в «малом» (т. е. при малых начальных отклонениях), если отрицательны все вещественные корни характеристического уравнения системы, составленного для ее линейного приближения.

2. Нелинейная система неустойчива в «малом», если хотя бы один корень характеристического уравнения линейного приближения имеет положительную вещественную часть.

При наличии чисто мнимых корней указанного уравнения вопрос об устойчивости системы требует в каждом случае дополнительного исследования.

Для нелинейных систем устойчивость «в малом» еще не решает вопроса об устойчивости системы в любых обстоятельствах: нелинейные системы могут быть устойчивы «в малом», т. е. при небольших начальных отклонениях от устойчивого состояния, и в то же время неустойчивы «в большом», когда начальное отклонение велико. Следовательно, устойчивость нелинейных систем зависит и от величины возмущения.

В линейных и линеаризированных системах в отличие от нелинейных устойчивость не зависит от величины возмущения.

Возможные виды кривых переходного процесса свободной составляющей x_c(τ) для устойчивой линейной системы приведены на рис 6.1,а, а для неустойчивой системы— на рис. 6.1,б.

При аналитическом исследовании динамических свойств системы регулирования необходимо найти ее дифференциальное уравнение и затем его проинтегрировать. Это означает, что тем самым будет найден закон изменения во времени интересующей нас величины.

Однако решение дифференциальных уравнений высоких порядков, даже для линейных систем, сопряжено с значительными трудностями.

Поэтому приобретают существенное значение признаки, по которым оказывается возможным судить об устойчивости систем регулирования без непосредственного интегрирования дифференциального уравнения, определяющего анализируемую систему.

Эти признаки получили название критериев устойчивости. Критерии устойчивости позволяют, не

прибегая к решению дифференциального уравнения системы, установить, является ли система устойчивой. Кроме того, такие критерии позволяют выяснить характер влияния того или иного параметра и структуры системы на ее устойчивость.

Для того чтобы лучше уяснить, от чего зависит устойчивость или неустойчивость системы регулирования, рассмотрим общее дифференциальное уравнение линейной системы автоматического регулирования.

В соответствии с определением устойчивости системы последняя характеризуется свободными движениями системы. Так как свободное движение линейной системы описывается однородным дифференциальным уравнением, т. е. уравнением без правой части, то, следовательно, для определения устойчивости линейной системы и надлежит исследовать такое однородное уравнение.

Уравнение свободного движения линейной системы автоматического регулирования, разрешенное относительно исследуемой величины, обычно относительно отклонения регулируемого параметра от заданного значения, может быть записано так:

,(2.23)

где С₀, С₁,…, С_n—постоянные коэффициенты, определяемые параметрами системы регулирования. В операторной форме это же уравнение запишется:

.

Отсюда характеристическое уравнение будет иметь вид:

.(2.24)

Решение дифференциального уравнения (2.23) при всех вещественных корнях, как известно, имеет следующий вид:

, (2.25)

где А_i — постоянные интегрирования, определяемые параметрами системы и начальными условиями;

р_i—корни характеристического уравнения (2.24);

τ — время.

При наличии пары комплексных корней уравнения (2.24) в правую часть формулы (2.25) будет входить слагаемое

, (6.6)2.26

где А_i — начальная амплитуда;

φ_i — начальная фаза.

Из (2.25) и (2.26) следует, что динамические свойства системы регулирования определяются значениями р_i, и A_i,.

Если все корни характеристического уравнения (2.24) будут отрицательные вещественные или комплексные с отрицательной вещественной частью, то каждое слагаемое правой части выражения (2.25) будет с течением времени уменьшаться и при , будет стремиться к нулю. Но если каждое слагаемое правой части этого выражения стремится к нулю приτ, стремящемся к бесконечности, то и сумма их будет также стремиться к нулю и условие (2.22) будет удовлетворяться.

Г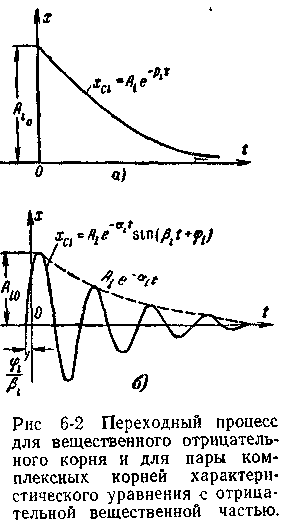рафическое представление изменения каждого слагаемого, соответствующего вещественному отрицательному корню, приведено на рис. 6.2,а, а для каждой пары комплексных корней с отрицательной вещественной частью — на рис. 6.2,б.

Система с такими корнями будет устойчивой, ибо отклонение параметра регулирования от заданного значения с течением времени уменьшается до нуля.

Если среди корней характеристического уравнения (6.4) будет хотя бы один вещественный положительный корень или если это уравнение будет иметь хотя бы одну пару сопряженных комплексных корней с положительной вещественной частью, то одно из слагаемых правой части формулы (6.5) или слагаемое, определяемое выражением (6.6), соответствующее этому корню (или паре корней), с течением времени будет неограниченно расти и при τ, стремящемся к бесконечности, будет само стремиться к бесконечности.

Переходный процесс для одного слагаемого правой части выражения (2.25), показатель степени в котором является вещественным положительным корнем, приведен на рис. 6.3,а, а переходный процесс для слагаемого, соответствующего паре комплексных сопряженных корней с положительной вещественной частью,— на рис. 6.3,б.

Это означает, что при наличии хотя бы одного такого слагаемого правая часть выражения (2.25) с течением времени будет неограниченно расти. Такая система, очевидно, уже не будет устойчивой, ибо отклонение параметра регулирования от заданного значения с течением времени неограниченно возрастает.

Если среди корней характеристического уравнения (2.24) будет хотя бы одна пара комплексных корней с вещественной частью, равной нулю, то появится составляющая вида (2.26), у которой показатель степени αi, будет равен нулю, и переходный процесс для нее будет иметь вид незатухающих колебаний. Пример такого переходного процесса приведен на рис. 6.4.

В этом случае система будет находиться на границе устойчивости и неустойчивости, но так как в переходном процессе такой системы раз возникшие колебания не будут затухать, то систему следует считать неустойчивой.

Таким образом, необходимым и достаточным условием устойчивости системы регулирования является соблюдение того, чтобы все корни характеристического уравнения системы имели отрицательную вещественную часть.

Если представить корни характеристического уравнения на комплексной плоскости, то для устойчивой системы требуется, чтобы все корни лежали в левой полуплоскости, как это показано на рис.6.5.

Очевидно, что при изменении параметров системы будут изменяться и коэффициенты С_i характеристического уравнения (2.24), а изменение коэффициентов уравнения будет вызывать перемещение корней на комплексной плоскости. При определенных значениях коэффициентов уравнения часть корней может оказаться расположенной на мнимой оси.

Совокупности значений коэффициентов характеристического уравнения, при которых по крайней мере одна пара комплексных корней находится на мнимой оси, а все остальные корни расположены левее ее, определяют точки границы устойчивости. Такому случаю, например, и соответствует переходный процесс, изображенный на рис. 6.4.

Граница устойчивости делит все совокупности значений коэффициентов характеристического уравнения на две области — одна из них соответствует устойчивости системы, а другая — ее неустойчивости.