Теория резонанса
Ψмолекулы = С1Ψ1 + С2Ψ2 + ... + СnΨn
В отличие от полного метода ВС, в теории резонанса учитывают не все базисные функции (резонансные формы), а только их небольшое число.
|
+1 |
–2 |
+1 |
|
|
||
Н О Н |
Н О Н |
Н О Н |
|
«ковалентный» |
Реальная |
«ионный» |
(атомный) тип" |
молекула |
тип РФ |
РФ |
|
|
Н• •О• •Н |
+ |
|
|
|
|
|
– |
|
|
+ |
+1 |
–2 |
+1 |
|||
Н |
|
|
|
|
|
О |
|
|
|
|
|
Н |
Н |
:О: |
Н |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
Ψк |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ |
|
|
Ψмолекулы = СкΨк + СиΨи |
|
и |
|
||||||||||||
|
|
|
|
|||||||||||||
Реальная молекула — это «резонансный гибрид» или «мезомерная (т.е. промежуточная) структура», в которой:
а) на атомах водорода будет наблюдаться избыточный положительный заряд (пропорциональный квадрату коэффициента Си);
б) на атоме кислорода будет наблюдаться избыточный отрицательный заряд (пропорциональный удвоенному квадрату коэффициента Си);
в) порядки ковалентных связей О • • • Н будут иметь величину между 1 и 0 (пропорционально квадрату коэффициента Ск).
О С О |
– |
+ |
– |
–1 |
+2 |
–1 |
О |
С |
О |
О |
С |
О |
|
Ковалентная РФ |
Молекула |
Ионная РФ |
||||
С О |
– |
+ |
–1 |
+1 |
С |
О |
С |
О |
|
Ковалентная РФ |
Молекула |
Ионная РФ |
||
Ковалентная |
Молекула |
Ковалентная |
|
РФ № 1 |
РФ № 2 |
||
|
Максимальное |
Максимальное |
отклонение |
отклонение |
влево |
вправо |
Равновесное
положение
АТОМЫ 
МОЛЕКУЛА 
ИОНЫ
II. Метод МО (молекулярных орбиталей)
АO MO
+10
Атом Ne |
Молекула Н–О–Н |
Молекула — деформированный атом
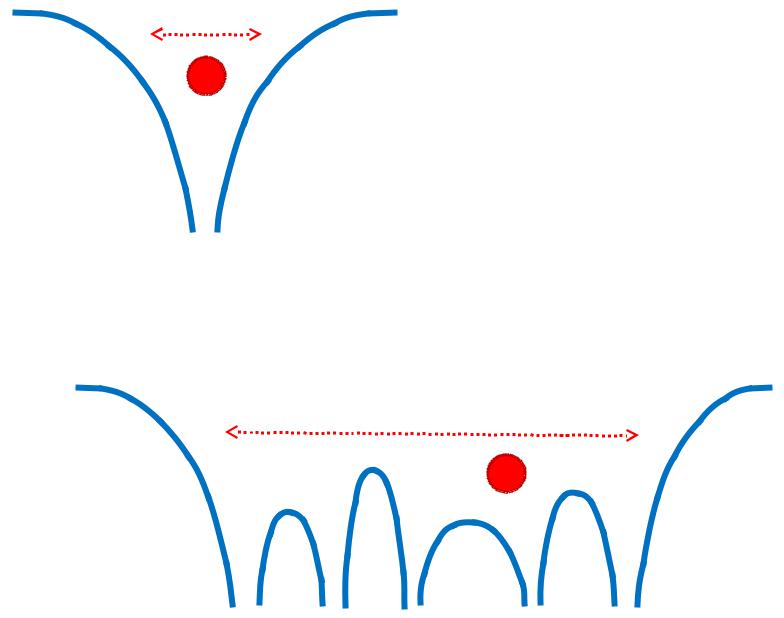
Одноядерная потенциальная яма (атом)
Многоядерная потенциальная яма (молекула)
Электронная оболочка молекулы в методе МО
Глобальное описание Φ(x1, y1, z1, η1,
x2, y2, z2, η2,
... ,
xn, yn, zn, ηn)
E
L
S
J
Локальное описание φ1(x1, y1, z1, η1) φ2(x2, y2, z2, η2)
... ,
φn(xn, yn, zn, ηn)
1, 2, ... , n1, 2, ... , n s1, s2, ... , sn j1, j2, ... , jn
Одноэлектронное приближение
Каждому электрону приписывается:
• индивидуальная функция — «молекулярная орбиталь» (МО)
φi (xi, yi, zi, ηi)
•набор одноэлектронных наблюдаемых
i ji i si
Спин-орбиталь (МСО) Орбиталь (МО)
φi (xi, yi, zi, ηi) = ψi (xi, yi, zi) χi (ηi)
Пространственный Спиновой множитель множитель
Глобальная волновая функция молекулы
1
Ф = —— n!
φ1(1) φ2(1) φn(1) φ1(2) φ2(2) φn(2)
. . . . . . . . .
φ1(n) φ2(n) φn(n)
Определитель
Слэтера
Каков явный вид МО?
|
1 |
= С11 1 |
+ С12 2 |
+ … + С1n n |
Вариант |
2 |
= С21 1 |
+ С22 2 |
+ … + С2n n |
МО ЛКАО |
…………………………………………. |
|||
|
n = Сn1 1 |
+ Сn2 2 |
+ … + Сnn n |
|
То же самое можно записать в матрично-векторной форме:
1 |
|
С11 |
С12 |
… С1n |
|
1 |
2 |
= |
С21 |
С22 |
… С2n |
• |
2 |
… |
|
………………. |
|
… |
||
n |
|
Сn1 Сn2 … Сnn |
|
n |
||
МО |
|
|
|
|
|
АО |
или в операторной форме: |
= С • |
|
||||
где С — «атомно-молекулярный оператор» (матрица)
Один атом может поставлять несколько АО в базисный набор
= ?
1 |
|
2 |
3 |
|
|
5 |
|
|
|||||
|
|
|||||
|
|
4 |
||||
= С1 1 + С12 2 + … + С5 5