
Лабораторная работа №1
Преломление света на сферической поверхности и определение фокусных расстояний тонких линз
Цель работы: изучение законов преломления лучей на сферической границе раздела двух сред, получение изображений и определение фокусных расстояний тонких линз.
Приборы и принадлежности: оптическая скамья с осветителем и светофильтром, объект-сетка, положительная и отрицательная линзы, экран.
Введение
Теория большинства оптических приборов базируется на представление о световых лучах, распространяющихся прямолинейно в однородном веществе и подчиняющимся законам отражения и преломления света на границе раздела двух сред. Раздел оптики, рассматривающий теорию таких приборов, называемых лучевой или геометрической оптикой.
Каждая светящаяся точка источника света в геометрической оптике рассматривается как вершина расходящегося пучка лучей, называемого гомоцентрическим, т.е. имеющим общий центр. Если после отражения и преломления этот пучок превращается в пучок, сходящийся в одной точке, то и последний является гомоцентрическим пучком, а его центр называется изображением светящейся точки. При сохранении гомоцентричности каждая точка источника дает одну точку изображения. Такие изображения называются точечными или стигматическими.
В силу обратимости световых лучей изображение можно рассматривать как источник, а источник как изображение. При стигматическом изображении. Центры малых пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся.
Соответственные лучи и пучки также называются сопряженными. Поверхность, нормальная к лучам, называется волновой поверхностью. Волновая поверхность гомоцентрического пучка в однородной изотропной среде есть, очевидно, сферическая поверхность.
Если в результате отражения и преломления в оптической системе пучок перестает быть гомоцентрическим, то волновая поверхность перестает быть сферической. Стигматичность изображения точки перестает быть точечным.
Задача практической оптики заключается в получении изображений, точно передающих форму источника (предмета), поэтому важнейшим вопросом лучевой оптики является создание и сохранение условий гомоцентричности пучков.
Краткая теория
преломления и отражения света на сферической поверхности
Подробное рассмотрение этого вопроса важно потому, что в качестве преломляющих и отражающих поверхностей в большинстве оптических приборов применяются плоские или сферические поверхности, т.к. изготовление и качественная обработка поверхности другой формы значительно сложнее.
Пусть две однородные среды с показателем преломления и разделены сферической поверхностью с радиусом кривизны и центром кривизны , рис.1.
Прямая , проходящая через центр кривизны и точечный источник (или произвольно выбранную точку произвольного источника), называется главной оптической осью сферической поверхности.
Изображением т. , лежащей на главной оптической оси, будет т. , лежащая, согласно закону преломления, так же на главной оптической оси.
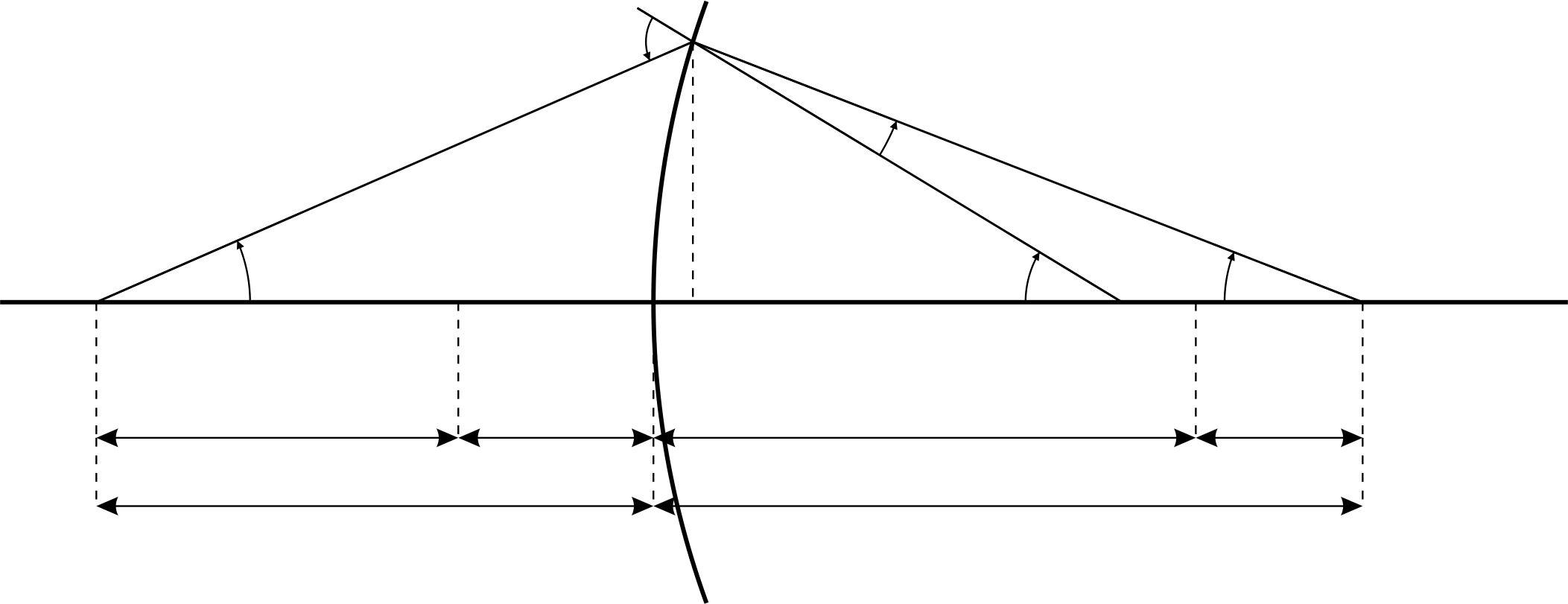
Рис.1.
Используя законы преломления и отражения света при построении изображений в оптических системах, здесь и в дальнейшем, условимся пользоваться следующими правилами знаков для углов и расстояний:
а) все расстояния отсчитываются от вершины сферической поверхности (точка пересечения главной оптической оси со сферической поверхностью) и считаются положительными, если они направлены в сторону распространения света от источника и сферической поверхности;
б) углы отсчитываются от направления главной оптической оси (или нормали к сферической поверхности) и считаются положительными, если они отсчитываются по часовой стрелке.
На чертеже будем отмечать только положительные значения длин и углов. Если какая-нибудь величина по принятому условию отрицательна, то для получения положительной величины перед ней будем ставить знак минус.
Рассмотрим узкий гомоцентрический пучок лучей, падающий из т. на поверхности раздела двух сред. Положим пучок настолько узким, что практически можно считать отрезок равным , а равным и т. д. такие лучи, составляющие с главной оптической осью малые углы, называются параксиальными (приосевыми).
По закону преломления:
(1)
Для параксиальных лучей .
Заменяя в формуле (1) синусы углов через углы, получим:
(2)
Из треугольника и (рис. 1) имеем:
, (3)
Подставляя (3) и (2) и учитывая, что , , , получим:
(4)
При преломлении величина , как видно из (4), сохраняет свое значение. Она носит название нулевого варианта Аббе.
Удобнее, представить формулу (4) в следующем виде:
(5)
Величина называется оптической силой преломляющей поверхности.
Из формулы (5) следует, что при соблюдении параксиальности лучей заданной величине вне зависимости от соответствует определенное значение . Это значит, что все лучи параксиального пучка исходящего из точки соберутся в сопряженной точке , т.е. преломленный пучок так же будет гомоцентрическим.
Если (предмет находится на бесконечно большом расстоянии), то:
(6)
Точка , где соберутся параксиальные лучи, идущие из бесконечности (или лучи, идущие параллельно главной оптической оси), называется вторым главным фокусом преломляющей поверхности.
Расстояние называется вторым главным фокусным расстоянием. Первым главным фокусом назовем точку, удовлетворяющую следующему условию: при помещении в эту точку точечного источника после преломления должен возникнуть пучок параллельных лучей (т.е. ). Расстояние равно:
(7)
Разделив правые и левые части (6) и(7), друг на друга, получим:
(8)
Разделив правую и левую часть равенства (5) на величину получим:
(9)
Формуле (9) можно придать несколько иной вид. Для этого введем в рассмотрение отрезки, определяющие положение точек и относительно фокусов и . Соблюдая правило знаков (расстояние и отсчитываются от соответствующих фокусов), из рис. 1 имеем:
, (10)
Подставляя эти значения в формулу (9), получим после преобразований:
(11)
Формула (11) называется формулой Ньютона.
Сравнивая (5), (6) и (7) легко убедиться, что:
(12)
Результаты, полученные для преломляющих сферических поверхностей могут быть применены и для отражающих сферических поверхностей (сферических зеркал), если использовать введенное ранее правило знаков для углов, (рис. 2).

Рис. 2.
По закону отражения:
(13)
Соотношение (13) формально может быть получено из закона преломления (1), если положить .
(14)
На основании этого можно сделать вывод, что любую формулу, выведенную для преломляющей поверхности, можно использовать для описания явлений в сферических зеркалах, если учесть соотношение (14).
Так, формула (5) для сферического зеркала примет вид:
(15)
Случай вогнутого и выпуклого зеркала отличается лишь знаком величины . Легко видеть, что фокус вогнутого зеркала – действительный (в нем пересекаются отраженные лучи), а фокус выпуклого зеркала – мнимый (в нем пересекаются продолжения отраженных лучей). В отличие от преломляющей сферической поверхности, сферическое зеркало имеет только один фокус. Правило знаков при определении величин , , , – те же, что и в случае преломляющих сферических поверхностей.
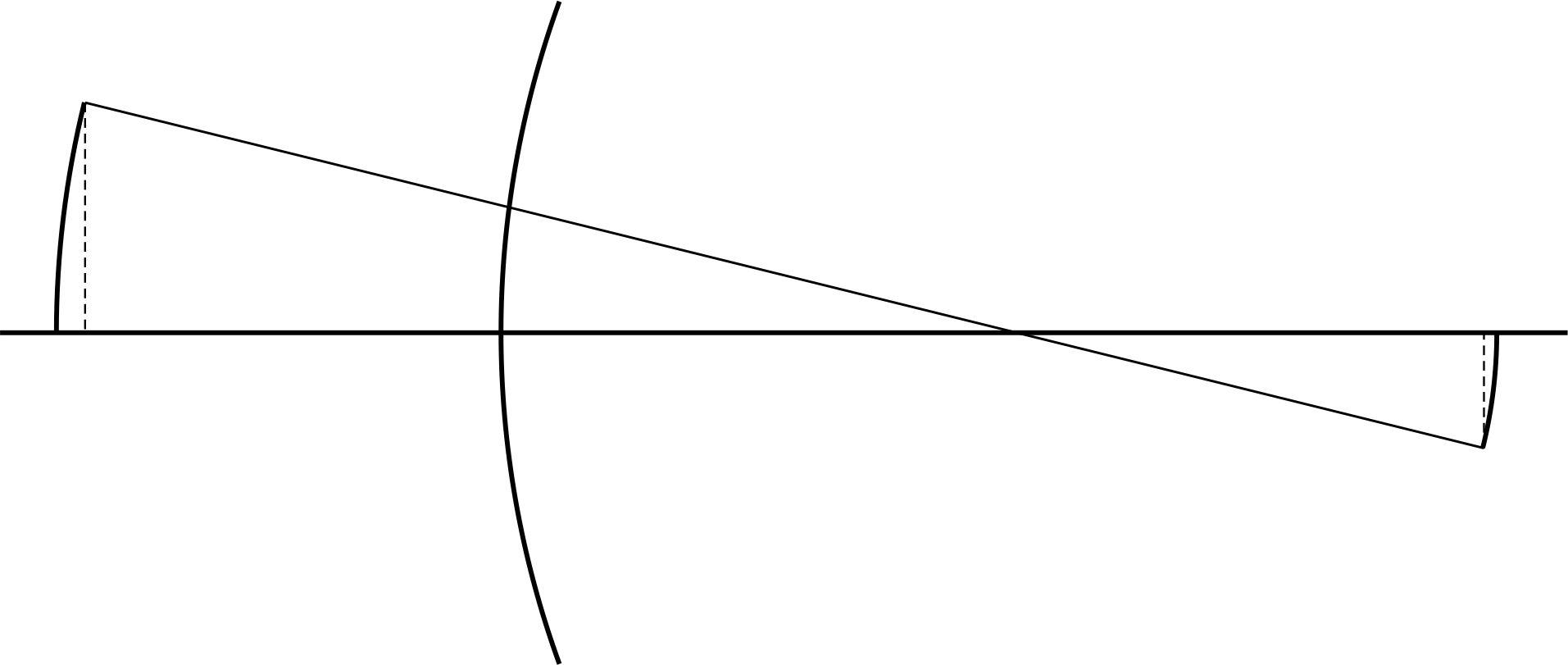
– точечный объект, – его изображение
Рис. 3.
Посмотрим, как при преломлении на сферической поверхности изображается отрезок прямой, перпендикулярной оптической оси.
Посмотрим, как при преломлении на сферической поверхности изображается отрезок прямой, перпендикулярной оптической оси. Повернем ось вокруг центра кривизны на малый угол . При этом точка опишет дугу , а точка – дугу . Все точки дуги отразится соответствующими точками дуги . В силу малости этих дуг, заменим их прямолинейными отрезками и , перпендикулярными к оси (по построению оптическая ось перпендикулярна дугам и ).
Таким образом, изображением малого отрезка перпендикулярного оптической оси, является отрезок , также перпендикулярной к оси. Отсюда вытекает и другой, достаточно очевидный вывод: изображение плоской поверхности , нормальной к оптической оси, есть поверхность , также нормальная к оптической оси.
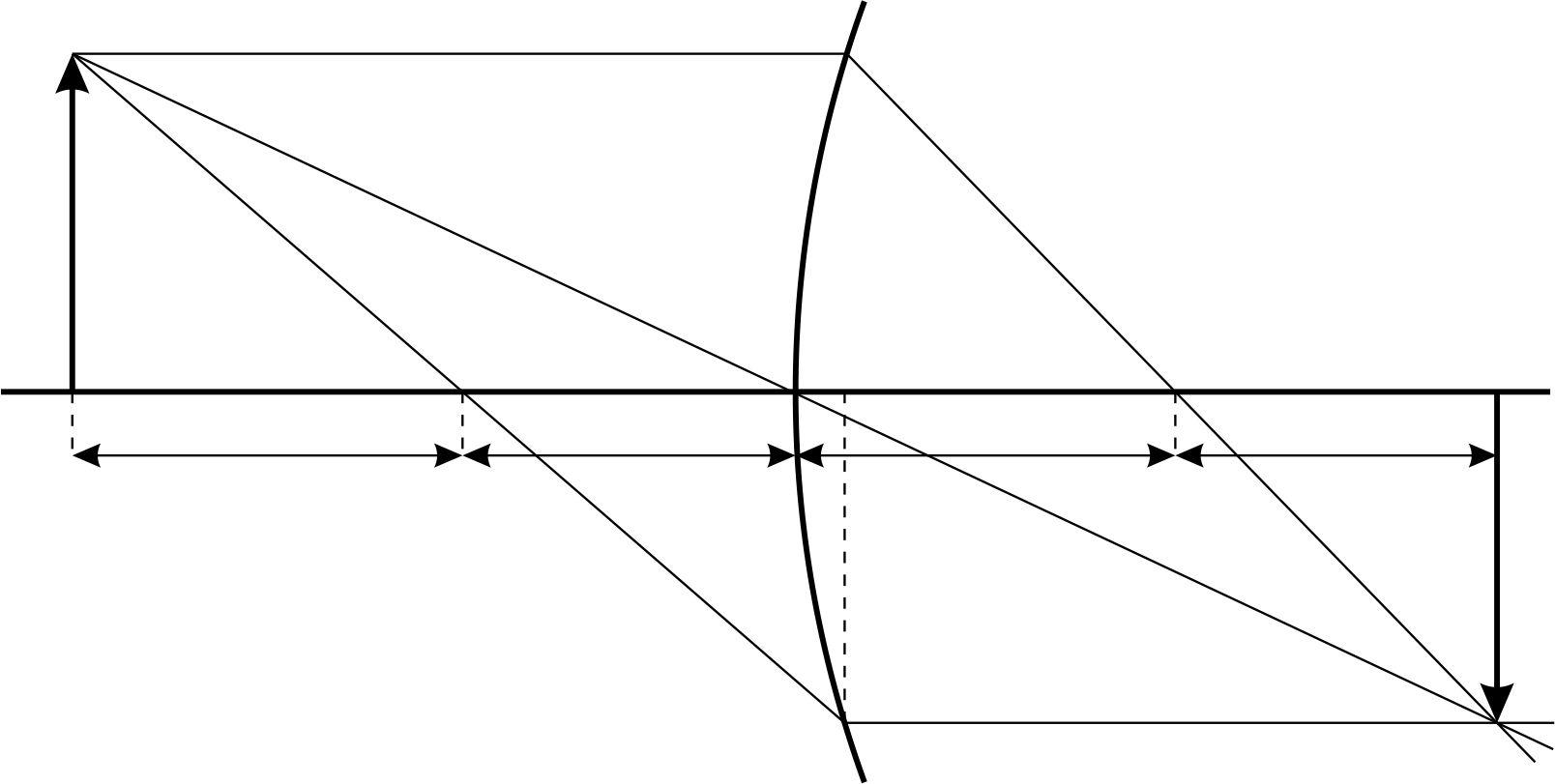
Рис. 4
Каждая точка изображения является местом пересечения всех лучей, исходящих из соответствующей точки предмета, прошедших через линзу. Для построения изображения точки, достаточно найти пересечение любых двух лучей, ход которых заранее известен. Такими лучами являются:
-
Луч, проходящий через оптический центр линзы – не преломляется и не изменяет своего направления;
-
Луч, параллельный главной оптической оси линзы – после преломления в линзе идет через фокус ;
-
Луч, проходящий через фокус – после преломления в линзе идет параллельно главной оптической оси линзы.
Для сравнительной характеристики объекта и его изображения введем понятие линейного и углового увеличения.
Назовем линейным увеличением отношение линейных размеров изображения к линейным размерам объекта:
(16)
Условимся считать отрезки, перпендикулярные к оптической оси положительными, если они направлены вверх, и отрицательными, если они направлены вниз.
Из треугольника и находим:
(17)
В основании (16) и(17) линейное увеличение:
(18)
Из теоремы Ньютона (11) имеем:
(19)
Преобразуем формулу линейного увеличения к другому виду. Для этого дополнительно проведем лучи так, как показано на рис.5
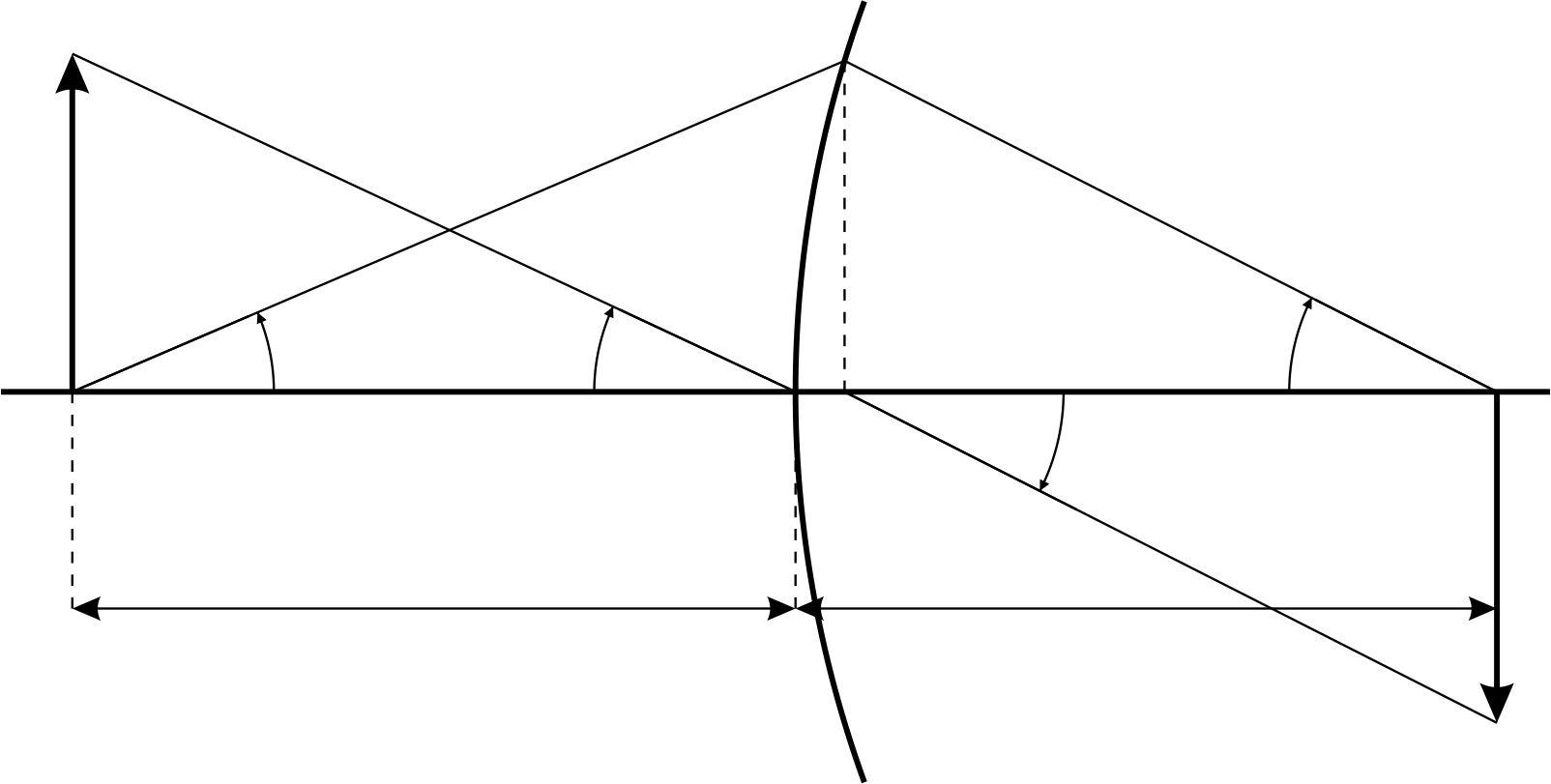
Рис. 5
Для параксиальных лучей (малых углов , , , ) из треугольников и вытекают следующие соотношения:
, (20)
Закон преломления для малых углов имеет вид:
(21)
Воспользовавшись последним уравнением системы (20) и соотношением (21), получим:
(22)
Из треугольников и для параксиальных лучей следует:
, (23)
Подставляя значение из (23) в (22), получим выражение для линейного увеличения:
, (24)
которое может быть переписано в следующем виде:
(25)
Произведение носит название инварианта Лагранжа-Гельмгольца.
Угловым увеличением называется величина, равная отношению тангенсов углов, под которыми виден предмет с расстояний и :
(26)
Связь между линейным и угловым увеличением устанавливается на основании формул (24) и (25):
(27)
Таким образом, линейное увеличение обратно пропорционально угловому.
