Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора по терверу(все кроме 27) / Шпора по терверу
.doc|
1.Предмет
теории вероятностей.События.Алгебра
событий.Теория
вероятностей–раздел
математики, изучающий закономерности
случайных явлений.Разница между
закономерными и случайными
событиями.Закономерное
событие–это
событие, которое всегда осуществляется,
как только создаются определённые
условия.Закономерное
явление –
это система закономерных событий.Случайные
события–это
события, которые при одних и тех же
условиях иногда происходят, а иногда
нет.Однако случайные события подчиняются
некоторым закономерностям, которые
называются вероятностными
закономерностями, при этом надо
условится, что мы будем иметь дело не
со всякими случайными событиями, а с
массовыми,
то есть будем предполагать, что в
принципе можно создать много раз одни
и те же условия, при каждом из которых
могут произойти или нет некоторые
случайные события.Пусть при осуществлении
некоторых условий (N
раз), случайное событие A,
будет осуществляться N(А)
раз.Число N(А)
– называется частотой событий A,
а отношение
Относительная частота колеблется около определенного числа, которое характеризует данное случайное событие.Р(А) – вероятность события А. Примеры:1)Пусть случайное событие A – выпадение герба при одном подбрасывании симметричной однородной монеты,Р(А) = 1/2 – вероятность выпадения герба.2)Статистика рождений показывает, что мальчиков рождается несколько больше, чем девочек. Доля рождения мальчиков 0,51-0,52.Р(А) = 0,51; 0,51 – вероятность рождения мальчиков. События. Достоверное событие – событие, которое всегда происходит (Ω).Невозможное событие – событие, которое не происходит никогда ().Событие Ā – событие противоположное событию A. Ā происходит тогда и только тогда, когда не происходит событие A.Суммой событий A и B называется событие A+B, которое происходит тогда и только тогда, когда происходит или A, или B, или оба вместе. Произведением событий A и B называется событие AB, которое происходит тогда и только тогда, когда происходят A и B вместе.Разностью событий A и B называется событие A-B, которое происходит тогда и только тогда, когда происходит A и не происходит B.События A и B несовместны, если AB=.Событие A влечет за собой событие B, если из наступления события A следует наступление события B (A B).События A и B называются равносильными A=B, если выполняются одновременно два включения A=B A B и B A.Пример: Бросается игральная кость. A = {выпадает четное число очков} и B = {выпало число очков, не большее трех}Решение: Выпало число очков отличное от 5 (A+B).Выпало 2 (AB).Выпало число очков равное 4 или 6 (A-B).Выпадает нечетное число очков (Ā). 3.Конечное
вероятностное пространство. Классическое
определение вероятности. Рассмотрим
случай конечного вероятностного
пространства. В этом случае
состоит из конечного числа элементарных
событий .
= {}
A
– алгебра всех подмножеств
(ввиду конечности вероятностного
пространства алгебра автоматически
является -алгеброй),
тогда вероятность P(A)
для любого подмножества A
задаем следующим образом. Пусть заданы
неотрицательные числа P,
которые удовлетворяют следующему
требованию
Замечание:Модель вероятностного пространства, приводящая к классическому определению вероятностей, когда элементарные события обладают свойствами «симметрии». Пример:Бросается кубик на стол. 1 = {выпадает 1} 2 = {выпадает 2} – свойства симметрии
9.Формула полной вероятности Система событий A1,…,An называется конечным разбиением(разбиением) пространства , если они: 1)попарно несовместны, т.е. AiAj=, если i j. 2) A1+A2 +… An =. Теорема (Формула полной вероятности) Если
A1,…,An
–
разбиение
и все P(Ai)>0,
то для всех событий B
Доказательство:B=B=B(A1+…+An)=BA1+…+BAn
Пример. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность события B={второй вынутый шар белый}. A = {первый шар белый}. Ā={ первый шар черный} Решение A Ā = , A + Ā =
Пример показывает, что при правильно организованной жеребьевке шансы будут равны. 8.Условные вероятности; теорема умножения N – число испытаний; A, B, AB – события; N(A), N(B), N(AB) – частоты событий;
Если
все относительные частоты событий
устойчивы, тогда условная относительная
частота тоже устойчива. Пусть
P(B)>0.Условной
вероятностью
P(A|B)
события A
при условии, что событие B
произошло, называется отношение
P(A|B) = PB(A) (встречается в литературе). Теорема умножения
Если P(A)>0,
P(B)>0,
а P(A|B),
то вероятность произведения
Доказательство: Доказательство следует из определения. Пример: 1 способ. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность того, что оба шара будут белыми. A = {1 вынутый шар белый} B = {2 вынутый шар белый} AB = {оба шара белых}
2 способ.
Следствие.
Пусть события
A1,…,An
таковы,
что
P(A1…An-1
)>0 тогда Доказательство: Доказательство проводится методом математической индукции.
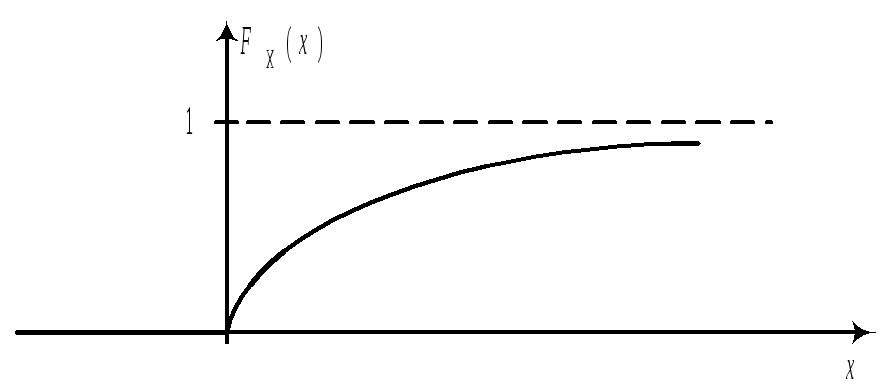
13.Функция распределения случайной величины. Её свойства. Функция распределения СВДТ. Ряд распределения может быть построен только для СВДТ, для недискретных случайных величин из-за несчетности множества возможных значений такое представление невозможно. Наиболее общей формой закона распределения пригодной для всех типов случайных величин является функция распределения. Функция F(x)=Fx(x)=P{X<x}, xR называется функцией распределения СВ Х. С помощью функции распределения можно выразить вероятности попадания CB Х в различные интервалы вида x1X< x2 , x1X x2 , x1<X x2 , x1<X< x2 . Пусть x1 < x2 , тогда {X< x2} разложим в сумму двух несовместных событий {X<x2}={X< x1}+{ x1 X<x2}, тогда P{X<x2}=P({X< x1} +{ x1 X<x2})=P{X< x1}+
P{
x1
X<x2};
FX(x2)=FX(x1)+
P{
x1Xx2};P{
x1Xx2}=
FX(x2)-FX(x1)
(**) Событие {X>x}
можно представить, как счетную сумму
несовместных событий
P{X>x}=1- FX(x+0); P{Xx}=1- P{X>x}=FX(x+0); P{x1Xx2}=FX(x2+0)- FX(x1); P{ x1Xx2}=FX(x2+0)- FX(x1+0);P{ x1Xx2}=FX(x2)- FX(x1+0); P{ X=x}=FX(x+0)- FX(x); Теорема. Функция FX(x) обладает следующими свойствами: 1. FX(x) – не убывает; 2. FX(x) – непрерывна слева; 3. FX(+)=1; 4. FX(-)=0;. Доказательство 3 и 4: 1.Следует из (**), т.к. P{x1Xx2 }0. 2.Следует из аксиомы непрерывности 4, т.к. события
FX(x)= FX(x-0) . Свойства 3, 4 вытекают из аксиомы счетной аддитивности (3*), т.к. =ΣAn (-<n<), где An={ n-1X()<n}, тогда
Пусть (0
FX(N)
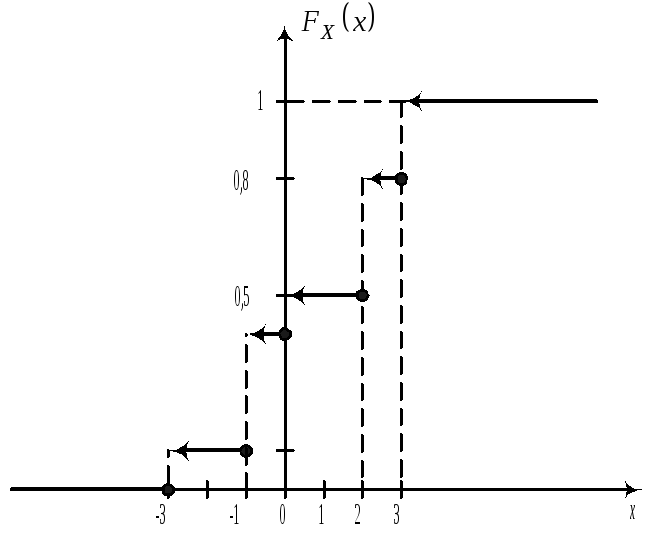
1 ) Из равенства P{X=x}=FX(x+0)-FX(x) следует, что в точках разрыва функции FX(x) имеет место положительная вероятность. P{X=x}>0 Так как при каждом натуральном n может быть не более n-точек x с вероятностями P{X=x}1/n, то у функции FX(x) имеется не более счетного числа точек разрыва.Обозначим через x1,x2,.. все точки разрыва функции FX(x), если вероятности P{X=x}=Pk таковы, что Σpk=1, то это равносильно тому, что СВ X имеет дискретное распределение, то есть является СВДТ.Замечание. Для СВДТ FX(x) имеет ступенчатый вид. Пример. X -3 -1 0 2 3 P 0,1 0,3 0,1 0,3 0,2 Получить функцию распределения и построить ее график. Решение. FX(x)=P{X<x}, т.е. FX(x)=0(x-3); FX(x)=0,1(-3<x-1); FX(x)=0,4(-1<x0); FX(x)=0,5(0<x2); FX(x)=0,8(2<x3); FX(x)=1(x>3);
P{X=2}= FX(2+0)- FX(2)=0,8-0,5=0,3; P{-1<X2}=FX(2+0)-FX(-1+0)=0,8-0,4=0,4 Введем новое важное понятие индикатора события. Опр:Индикатором
события A
A
называется
СВ : Ряд распределения случайной величины IA имеет следующий вид
где р-вероятность события А.
16.Моменты n-го порядка. Дисперсия. Среднее квадратическое отклонение. МО в теории вероятностей относится к типу характеристик положения (см. далее мода, медиана), кроме них используется еще ряд числовых характеристик различного назначения, среди них особое значение имеют моменты (начальные, центральные).Положим g(x)=xS. Опр.Начальным моментом S-го порядка СВ Х называется S=M[XS]. Замечание: Иногда используются абсолютные начальные моменты S-го порядка M[XS].
Для СВДТ:
Для СВНТ:
Замечание.
Обозначим
Определение.
Центральным моментом S-го
порядка называется
Замечание. Иногда используются абсолютные центральные моменты S-го порядка.
Для СВДТ:
Для СВНТ:
Определение.
Центральный момент II-го
порядка ( Для СВДТ:
Для СВНТ:
Опр. Свойства дисперсии:
1.
Доказательство:
2.
Доказательство:
По свойству 4 МО и с учетом неравенства (*) получаем доказательство свойства 2 для дисперсии.
3.
Доказательство:
Пусть на прямой в точках x1 <x2 <…<xk расположены точечные массы p1,p2., pk Σpi=1:
M[X]=Σxipi (1<i<k) – центр тяжести D[X]= Σ(xi-mi)pi (1<i<k) – момент инерции масс pi относительно центра тяжести. Таким образом, МО характеризует место, вокруг которого группируются массы pi, а дисперсия – степень разбросанности этих масс относительно МО.
21. Простейший Пуассоновский поток На практике часто встречаются ситуации, где имеет место распределение Пуассона. Задача. Пусть на оси времени 0t случайным образом возникают точки моменты появления каких-то однородных событий. (Например, вызовы на телефонной станции, приход посетителей в магазин и т.д.)). Последовательность таких моментов назовем потоком событий.Предположим, что поток обладает следующими свойствами. Свойства. 1)Стационарность.Это свойство означает, что вероятность попадания, того или иного числа событий, на участок времени длиной не зависит от того, где на оси 0t расположен этот участок, а зависит только от его длины .Из этого следует, что среднее число событий, появляющееся в единицу () времени , постоянно. – интенсивность потока. 2)Ординарность.Это свойство заключается в том, что вероятность попадания на малый участок t двух или более событий пренебрежимо мала с вероятностью попадания на него одного события. Т.е. при t0 вероятность двух или более событий является бесконечно малой более высокого порядка малости, чем вероятность попадания на него одного события. 3)Отсутствие последствия.Это свойство означает, что вероятность попадания некоторого числа событий на заданный участок оси 0t не зависит от того сколько событий попало на любой другой не пересекающийся с ним участок (в частности “будущее” потока не зависит от его “прошлого”). Опр.Поток событий, обладающий этими 3-мя свойствами называется простейшим (или стационарным) Пуассоновским потоком. Покажем, как простейший Пуассоновский поток связан с распределением Пуассона.
СВ Х – количество событий, попадающих на участок 0t, длиной . Покажем, что Х имеет распределение Пуассона. Доказательство: Разделим участок длины на n равных частей t =/n. МО числа событий, попадающих на элементарный участок t, равно t*. Согласно свойству 2 (ординарности) можно пренебречь вероятностью попадания на элементарный участок t, двух или более событий. Назовем элементарный участок t – занятым, если на нем появилось событие из потока. Назовем элементарный участок t – свободным, если на нем не появилось событие из потока.A = {участок t занят} IA= 1(участок t занят) IA= 0 (участок t свободен). M[IA]=pt– вероятность того, что участок t занят. Среднее число, то есть МО числа событий, попадающих на участок длины t, будет равно M[IA]= t*. pt= t*. pt=*/n
Рассмотрим
теперь n-участков
на временной оси, как n-независимых
испытаний (опытов), в каждом из которых
(независимость этих испытаний
из свойства 3) может появиться событие
А
и вероятность этого события
СВ Х имеет биномиальное распределение
Будем
теперь неограниченно увеличивать
число элементарных участков и найдем
при
Согласно
теореме Пуассона, при
28.Оценка отклонения теоретического распределения от нормального; асимметрия и эксцесс.
При
изучении распределений, отличных от
нормального, возникает необходимость
количественно оценить это различие.
С этой целью вводят специальные
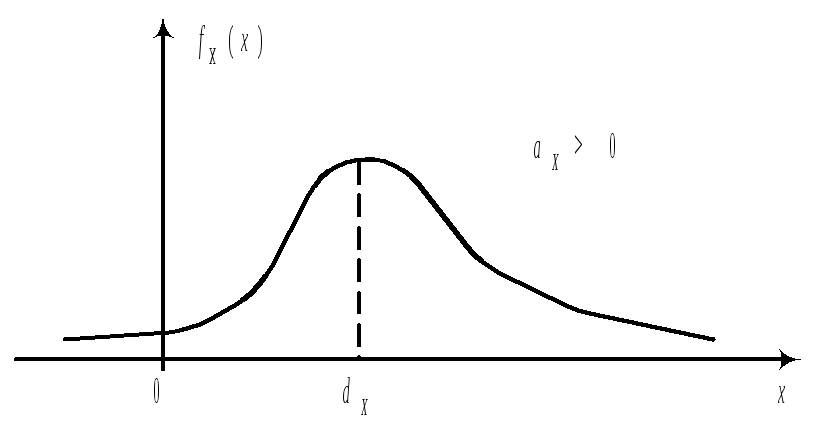
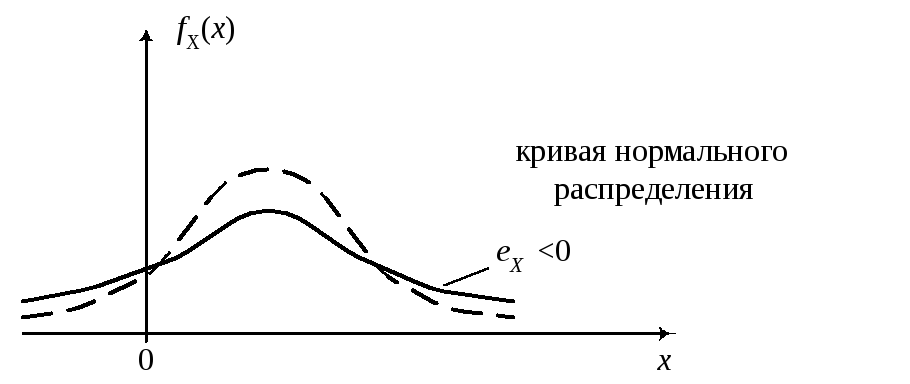
характеристики (асимметрию и эксцесс). Для нормального распределения эти характеристики равны 0, поэтому, если для изучаемого теоретического распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот большие значения aX и eX, указывают значительные отклонения от нормального.
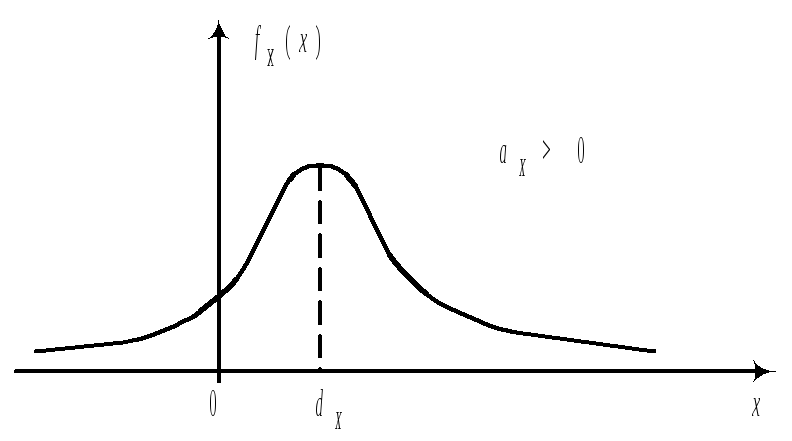
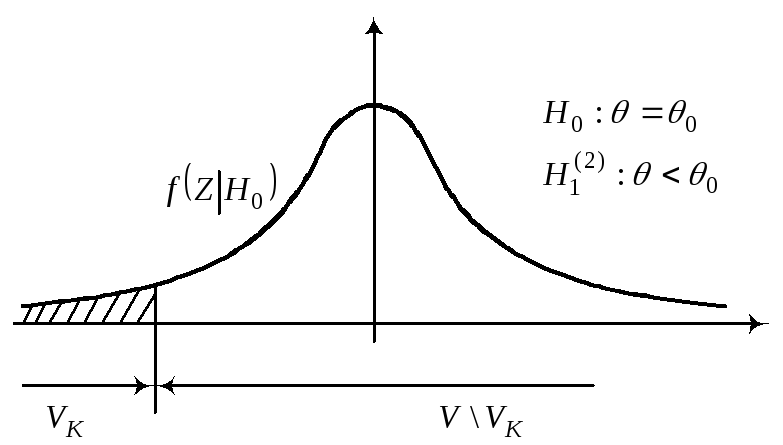
Пологая часть правее моды, значит aX>0.
Пологая часть левее моды, значит aX<0.
Замечание.При исследовании эксцесса надо считать, что нормальное исследуемое распределение, имеют одинаковое МО и дисперсию.
30.Дискретные двумерные случайные величины Опр. Двумерная СВ (X, Y) называется дискретной, если каждая из СВ и Х и Y является дискретной.
Пусть
СВ Х
может принимать значения
Двумерный
случайные вектор может принимать
только пары значений
По этой таблице нетрудно определить функцию распределения.
33.Условные законы распределения для системы СВ. Если СВ образующие систему зависимы, то для нахождения закона распределения системы не достаточно знать законы распределения отдельных величин, входящих в систему, требуется знать так называемый условный закон распределения одной из них. ОпрУсловным законом распределения одной из величин системы (X, Y) называется ее закон распределения вычисленный при условии, что другая СВ приняла определенное значение. Начнем с наиболее простого случая, а именно со случая, когда СВ Y является дискретной.
Опр.Условной
функцией распределения
Замечание 1.Условная функция распределения обладает всеми свойствами, которые присущи обычной (т.е. безусловной) функции распределения.
Замечание
2Если
СВ X
также дискретная, причем
В
общем случае условную функцию
распределения
Получим.
Назовем
условной функцией распределения
Оказывается
такой предел всегда существует.Если
СВ Y
– непрерывна, то условную функцию
распределения можно определить
следующим выражением
В
наиболее важных для приложений случаях
вектор (X,
Y)
представляет собой двумерную
непрерывную СВ с совместной плотностью
Так
как функция
36. Коэффициент корреляции. Связь между…
Теорема Если же СВ X и Y связывает жесткая функциональная линейная зависимость Y=aX+b, то XY=1 при a>0, XY= –1 при a<0.
Доказательство:
Теорема: XY1 Доказательство:
Рассмотрим СВ
Опр. СВ X и Y называется не коррелированными, если XY =0 (или KXY=0). Замечание.Из независимости СВ следует их не коррелированность. Обратное не верно. Из коррелированности не вытекает их независимость Теорема. D[X+Y] = DX+DY+2 KXY Доказательство: D[X+Y]=M[((X+Y)–(mX – mY))2]= M[((X– mX)+(Y – mY))2]= M[(X– mX)2+ 2(X– mX)( Y – mY)+ (Y – mY)2]= DX+DY+2 M[(X– mX)(Y – mY)]= DX+DY+2 KXY
Следствие: (доказательство проводится методом математической индукции).
40.Функции от многомерных СВ. Формула композиции.Функция от многомерной СВ определяется точно также, как и функция от одномерной СВ. Мы рассмотрим это понятие на примере двумерной СВ. Пусть на вероятностном пространстве (, A, P), задана двумерная СВ (X, Y). Предположим, что у нас имеется измеренная числовая функция g(X,Y) числовых аргументов X и Y. СВ Z=g(X,Y) = g(X(),Y()) , назовем функцией от двумерной СВ (X, Y). а) Функция g(X,Y)от двумерной дискретной СВ (X, Y) снова является дискретной СВ, принимающей значения g(xi , yj) с вероятностями Pij=P{X=xi ,Y=yj } Чтобы построить ряд распределения СВ Z=g(X,Y) надо:1) Исключить все те значения g(xi , yj) , вероятность которых равна нулю; 2) Объединить в один столбец все одинаковые значения g(xi , yj), приписав этому столбцу суммарную вероятность. б) В случае когда СВ (X, Y) непрерывного типа с плотностью f(x,y), функция распределения Z=g(X,Y) будет определяться формулой
Область интегрирования здесь состоит из всех точек (x, y) для которых g(X,Y)<Z. особо важным для практики представляется случай, когда X и Y – независимые СВ, а функция Z=X + Y, тогда g(x,y)=x+y. Получается так называемая формула композиции: fX(x) - ф-я плотности композиции от х fY(y) - ф-я плотности композиции от у f(x,y)= fX (x) fY (y)
Интеграл (*) вычисляется, как повторный, поэтому
Дифференцируя по z получаем
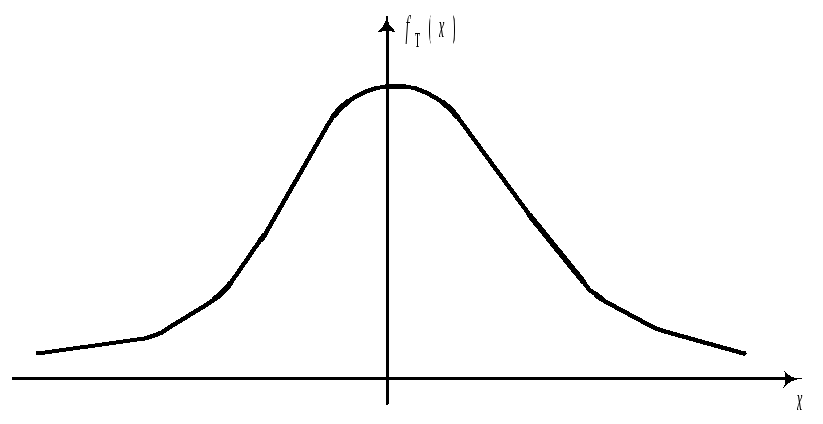
– формулы композиции (свертки). С помощью этих формул легко выражаются формулы плотности и функции распределения суммы независимых СВ. 42.Распределение Стьюдента.Пусть Z~N(0;1). V– независимая от Z СВ, которая распределена по закону 2 с k степенями свободы.
Рассмотрим
СВ
СВ
Т
имеет распределение, которое называется
t–распределением
или распределением Стьюдента с k
степенями свободы.
t–распределение определяется одним параметром – числом степеней свободы. С возрастанием числа степеней свободы t–распределение асимптотически (довольно быстро) приближается к стандартному нормальному распределению с параметрами (0; 1).
Для
СВ, имеющих распределение Стьюдента,
имеется таблица квантилей, причем в
силу четности
46.Выборка и способы ее представления Задачи математической статистики: Установления закономерностей, которым подчинены массовые случайные явления основано на изучении методами теории вероятностей статистических данных (результатов наблюдений)1. Задача математической статистики : Указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально составленных экспериментов.2. Задача математической статистики: 1) Разработать методы анализа статистических данных в зависимости от целей исследования: а) оценка неизвестной вероятности событий; б) оценка неизвестной функции распределения; в) оценка параметров распределения, вид которого известен; г) оценка зависимости СВ от одной или нескольких других СВ. 2) Проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения вид, которого известен. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности. Выборка и способы ее представления: Математическая статистика позволяет получить обоснованные выводы о параметрах, видах распределений и других свойствах СВ о конечной совокупности наблюдений над этими величинами. Выборка понимается следующим образом. Пусть СВ Х наблюдается на каком либо эксперименте, повторим этот эксперимент n раз при одинаковых условиях. Получаем Х1,.., Хn где каждая Хj – СВ соответствующая j-му эксперименту. Очевидно, что Хj – независимые в совокупности СВ, причем каждая из этих СВ имеет один и тот же закон распределения, что и СВ Х. Опр. Закон распределения СВ Х называется распределением генеральной совокупности. СВ вектор Х1,.., Хn называется выборочным вектором, а конкретные числа x1,.., xn, получаемые на практике при n кратном повторении эксперимента в неизменных условиях представляет собой реализацию выборочного вектора и называются выборкой объема n. Что такое вариационный ряд, размах выборки, статистический ряд, группированный статистический ряд, частоты, относительные частоты, накопленные частоты, относительные накопленные частоты, всевозможные полигоны и гистограммы, а также, что такое эмпирическая функция распределения изучили самостоятельно.
47.Числовые
характеристики выборки Пусть
x1,..,
xn
выборка объема n
из генеральной совокупности с функцией
распределения FX(x).
Рассмотрим выборочное
распределение,
т.е. распределение дискретной СВ,
принимающей эти значения с вероятностями,
равными 1/n.
Соответственно числовые характеристики
этого выборочного распределения
называют выборочными (эмпирическими)
числовыми характеристиками. Замечание.
Выборочные
числовые характеристики являются
характеристиками данной выборки, но
не являются характеристиками
распределения генеральной совокупности.
“~” – при обозначении этих числовых
характеристик.
51. Выборочная
дисперсия
Докажем, что
выборочная дисперсия является
смещенной оценкой для дисперсии
генеральной совокупности.
Выполним следующие преобразования
Найдем МО для дисперсии:
МО не совпадает с 2, а отличается на –2/n – смещение. Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину 2/n, правда это смещение сходит на нет при n . Чтобы устранить это смещение надо «исправить» дисперсию.
Можно доказать, что статистика S2 является и состоятельной оценкой для дисперсии генеральной совокупности.Замечание. К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.
54. Доверительный интервал для оценки МО при НЕизвестной дисперсии
2)Доверительный
интервал для оценки МО при неизвестной
дисперсии нормально распределенной
генеральной совокупности. Пусть
В
литературе по статистике показано,
что Y
имеет распределение Стьюдента с n–1
степенью свободы
По
заданной доверительной вероятности
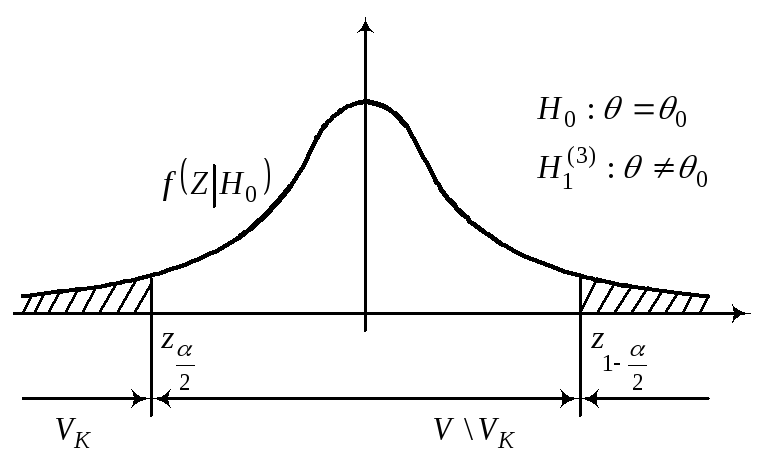
56. Проверка статистических гипотез Пусть Х – наблюдаемая СВ. Она может быть дискретной, а может и непрерывной. Опр. Статистической гипотезой Н называется предположение относительно параметров или вида распределения СВ Х. Гипотеза Н называется простой, если она однозначно определяет распределение СВ Х, иначе Н называется сложной. Если распределение СВ Х известно и по выборке наблюдений необходимо проверить предположение о значении параметров этого распределения, то такие гипотезы называются параметрическими. А гипотезы о виде распределения – непараметрические. Проверяемая гипотеза называется нулевой гипотезой и обозначается Н0. Обязательно на ряду с Н0 рассматривают одну из альтернативных гипотез Н1. При этом имеются различные ситуации для Н1.
Выбор альтернативной гипотезы Н1 определяется конкретной формулировкой задачи.
Опр.Правило,
по которому принимается решение
принять или отклонить гипотезу Н0,
называется критерием К.
Так как решение принимается на основе
выборки наблюдений СВ Х,
то необходимо выбрать подходящую
статистику, которую мы будем называть
статистикой Z
критерия К.Замечание.
При проверке
простой параметрической гипотезы
Н0:
=0
в качестве статистики критерия
выбирают ту же статистику, что и для
оценки параметра ,
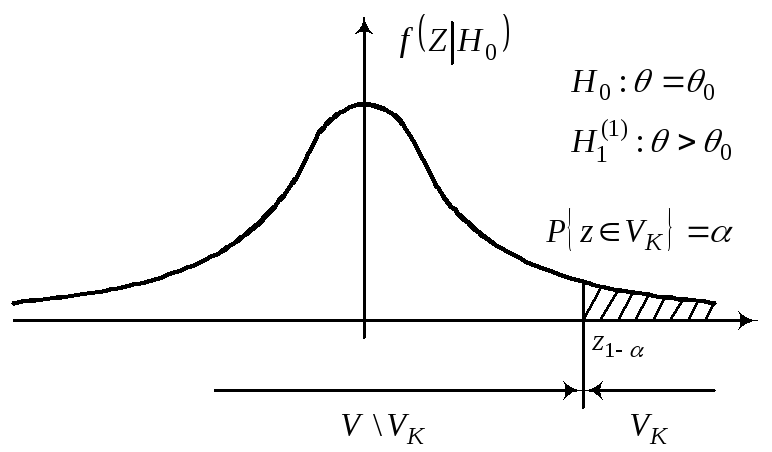
т.е. Отклонить гипотезу Н0, если zвVk. Отклонить гипотезу Н0, если zвV \ Vk. Уровень значимости определяет размер критической области, а ее положение зависит от альтернативной гипотезы Н1.
Z1––квантиль распределения Z при условии, что верна гипотеза Н0.
Z– квантиль распределения Z при условии, что верна гипотеза Н0.
Проверку параметрической гипотезы при помощи критерия значимости можно разбить на следующие этапы:1)сформулировать Н0 и Н1;2)назначить ;3)выбрать статистику Z для проверки Н0;4)определить выборочное распределение Z при условии, что верна Н0;5)определить VK (она зависит от Н1);6)получить выборку и вычислить zb ;7)принять статистическое решение: zвVk – отклонить Н0; zвV \Vk – принять Н0. Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов.Опр. Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н0 отклоняется, когда Н0 – верна. Вероятность P{ZVkH0}=..ОпрОшибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н0, но в действительности верна альтернативная гипотеза Н1. Вероятность ошибки второго рода при условии, что гипотеза Н1 – простая, P{ZV\VkH1}=.Проверка статистических гипотез и доверительных интервалов.Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н0 – принимается, если значение 0 накрывается доверительным интервалом, иначе отклоняется.
|
2.Вероятностное
пространство.Вероятность,ее
свойства.Теорема сложения.Тройка
(,
A,
P),
где
– это пространство элементарных
событий;A
– -алгебра
подмножеств ,
называемых событиями;P
– числовая
функция, определенная на событиях и
называемая вероятностью.P
называется вероятностным
пространством,
если выполнены следующие аксиомы:1)P(A)
0,AA.2)P()
= 1 (нормированность P).3)P(A+B)=P(A)
+ P(B),
если AB=
(аддитивность).4)Для любой убывающей
последовательности A1
A2
…
An…событий
из A
такой, что Из этих аксиом вытекают Свойства вероятностей: 1)Если A B, то вероятность P(B–A) = P(B) – P(A).
Разобьем событие B в сумму несовместных событий B=A+(B-A), A(B-A)=, P(B) = P(A+(B-A))=P(A)+P(B-A) (по аксиоме 3) P(B-A)=P(B) - P(A) . 2)Если A B, то P(A) P(B)Доказательство: Доказательство следует из 1 свойства и аксиомы 1. P(A) + P(B-A) = P(B) P(B-A) 0, следовательно P(A) P(B) . 3)A A 0 P(A) 1 Доказательство: A P(A) P(), P() = 1(по аксиоме 2) P(A) 0, A A(по аксиоме 1) . 4)P(Ā) = 1 - P(A) Доказательство: A+ Ā = , A Ā = Тогда по аксиоме 3 и аксиоме 2 получаем P(A+ Ā) = P(), P(A) + P(Ā) = P(), P(A) +P(Ā) = 1 P(Ā) = 1 - P(A) . 5) P() = 0Доказательство: + = Тогда по аксиоме 3 и 2 получаем, P() + P() = P() P() + 1 = 1, P() = 0 . 6)Теорема сложения A, B A : P(A+B) = P(A) + P(B) – P(AB)
Доказательство: A + B = A + (B - AB), A(B - AB) = P(A+B) = P(A) + P(B - AB), но AB B следовательно по первому свойству (вероятность от разности равна разности вероятностей). P(A+B) = P(A) + P(B) – P(AB) .
4.Основные правила комбиноторики:«правило суммы» и «правило произведения» Комбинаторика – это наука о том, сколько различных комбинаций удовлетворяющих условиям можно составить на элементах конечного множества. Комбинаторные схемы: Правило суммы: X – конечное множество X=n – количество элементов. Объект x из X может быть выбран n-способами. Пусть X1,…,Xk попарно непересекающиеся множества, то есть XiXj=, ij тогда очевидно выполняется равенство.
Правило
произведения:Если
объект x
может быть выбран m-способами
и после каждого из таких выборов
объект y
может быть выбран n-способами.
Тогда выбор упорядоченной пары (x,y)
может быть осуществлен – mn
способами. Доказательство: Воспользуемся
правилом суммы. {a1,…,am}–
множество элементов, из которых
выбирается объект x.i=1,..,m,рассмотрим
множество Xi={(ai
,y)},
тогда первая компонента совпадает с
ai.
Множества Xi
попарно не пересекаются. Xi=n.
Множество
пар Xi-это
объед.
В общем случае правило произведения формируется следующим образом: Если объект x1 может быть выбран n1 – способами, после чего объект x2 может быть выбран n2 способами и i, где i=1,..,m-1 (2 i m-1) после выбора объектов x1,…,xi объект xi+1 может быть выбран ni+1-способами, то выбор упорядоченной последовательности x1,…,xm может быть осуществлен n1,…,nm способами. Доказательство проводится методом математической индукции.
10.Формулы
Байеса Теорема.Если
A1,…,An
– разбиение
и все
Доказательство: По теореме умножения:
Формулы Байеса
можно интерпретировать следующим
образом: назовём Ai
– гипотезой, а B
– результат некоторого эксперимента,
a
P(Ai)
– априорные вероятности, а условные
вероятности
A1A2=,
A1+A2=
B={годная
деталь признана стандартной}
11. Независимость
событий Если
события A
и B
таковы, что P(B)>0
P(AB)
Определение.
Событие A
не зависит от события B,
если P(AB)
= P(A)
Если потребовать условия P(A)>0,
то Понятие того, что одно событие зависит от другого, симметрично. Замечание Из теоремы умножения: P(AB)=P(B) P(AB) P(AB)=P(B) P(A) Это приводит к определению. ОпределениеСобытия A и B называются независимыми, если вероятность произведения событий равна произведению вероятностей событий (P(AB)=P(A)P(B)). Если событие A не зависит от события B, то они являются просто независимыми. Если P(AB)=P(A)P(B) не выполняется, то события являются зависимыми. P(AB)=P(A)P(B)–теоретико-вероятностная (статистическая) независимость; её следует отличать от причинной независимости реальных явлений. Причинная независимость реальных явлений не устанавливается с помощью этого равенства, а постулируется на основе других внешних соображений. Определение (Независимость событий в совокупности) События A1,…,An называются независимыми, если индексов 1i1< i2<…< imn, где 2mn, то выполняется:
В противном
случае — события зависимы. Замечание.Из
определения независимости событий
в совокупности следует, что события
любого подмножества
Решение.P(A2)=1/2; P(A3)=1/2 ; P(A5)=1/2; P(A30)=1/2 P(A2A3)=1/4;P(A2A5)=1/4;P(A3A5)=1/4;P(A2A3A5)=1/4 P(A2A3)=P(A2)P(A3) P(A2A5)=P(A2)P(A5) - попарно независимы P(A3A5)=P(A3)P(A5) P(A2)P(A3) P(A5)=0.5*0.5*0.5=1/8 P(A2A3 A5)=1/4 (в совокупности зависимы). Совокупная независимость более сильное свойство, нежели попарная независимость.
Теорема.Если
события A1,…,An
являются
независимыми, индексы i1,…,in
, j1,…,jk
– все различны, вероятность
14. Непрерывная СВ. Плотность распределения.
Опр.Функция
Из определения (***) следуют свойства плотности распределения.
Свойства
1.
Замечание.
Для
СВ X
имеющей функции. Плотности из свойства
1 и теоремы из курса математического
анализа (о непрерывности интеграла
с переменным верхним пределом)
что
2.
3.
4.
5.
Условия нормировки:
Опр.
СВ X
называется СВНТ,
если ее распределение имеет функцию
плотности
Через
плотность
17.Мода, медиана и квантили МО не единственная характеристика положения, применяемая в теории вероятностей.
Опр.
Модой
СВДТ Х
называется такое возможное значение
xm,
для которого
Модой СВНТ Х называется действительное число dX, являющееся точкой максимума функции плотности вероятностей (fX (x)) Пример. X 0 1 2 3 4 P 0,05 0,3 0,25 0,2 0,2 dX=1 Замечание. Мода может не существовать, иметь единственное значение, такие распределения называются унимодальное, или иметь множества значений – полимодальное распределение. Наличие более чем одной моды, часто указывает на разнородность статистического материала, который положен в основу исследований.
Опр.Медианой
СВ Х
называется действительное число hX,
удовлетворяющее условию:
Эта характеристика применяется, как правило, только для СВНТ и геометрически медиана, это абсцисса той точки на оси ОХ, для которой площади под графиком fX (x)лежащие слева и справа от нее одинаковы и равны 1/2 Замечание. В случае симметричного распределения (имеющего моду) три характеристики: 1) МО ; 2) мода; 3) медиана совпадают. Замечание. Уравнение Fx(x)=1/2 может иметь множество корней, поэтому медиана может определяться неоднозначно. Опр. Квантильлью порядка р распределения СВНТ Х называется действительное число tp, удовлетворяющее уравнению P{X<tp}=p Замечание. Медиана hx=t0,5 – квантиль порядка 0,5.
22.Локальная предельная теорема Муавра-Лапласа.
Биномиальное
распределение имеет МО равное np
Пусть p – не близко к 0 и 1. Теорема.
Если
в схеме независимых испытаний
Замечание.
Эти таблицы даются, только для x>0.
18.Целочисленные СВ и их производящие функции В ряде случаев при определении важнейших числовых характеристик дискретных СВ может помочь аппарат производящих функций. Опр. Дискретную СВ Х, принимающую только целые, неотрицательные значения называют целочисленной СВ.
Закон
распределения целочисленной СВ
определяется
Закон распределения целочисленной СВ удобно изучать с помощью производящей функции, которая определяется, как
В
соответствии с определением МО:
Этот
ряд сходится абсолютно при
Поскольку
Замечание В математике рассматриваются произвольные производящие функции. a0, a1 ,a2... a0 +Sa1 +S2a2 +… – производящая функция, если она имеет не нулевой радиус сходимости.
Замечание Возьмем первую производную по S от производящей функции.
То есть можно выразить начальные моменты более высокого порядка, через начальные моменты более низкого порядка.
23 Интегральная предельная теорема Муавра-Лапласа Теорема.
При
Замечание.
Ее значения приводятся только для 0 x3,5. Ф(–x)=1– Ф(x) Пример.Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005).Чему равна вероятность, что из n = 10000 наудачу взятых изделий, бракованных окажется не более 70 (m = 70).
24.Геометрическое распределение Опр.СВДТ Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, …, m, …, а вероятности этих значений
Комментарий Вероятности Pm для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q.На практике геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых испытаний (опытов) с целью получения какого-то результата (“успеха”) А. При каждом опыте “успех” достигается с вероятностью p. СВ Х – это число безуспешных опытов до первой попытки, в которой появляется результат А. Ряд распределения имеет следующий вид. X 0 1 2 … m …. P p qp q2p ... qmp … Найдем числовые характеристики СВ Х распределенной по геометрическому закону.
На практике чаще приходится рассматривать не СВ Х, имеющую геометрическое распределение, а Y=X+1 – это число попыток до первого успеха, включая удавшуюся.Ряд распределения Y 1 2 … m …. P p qp … qm–1p … –геометрическое распределение,сдвинутое на 1 (геометрическое плюс1). mY=M[X+1]=M[X]+1=q/p+1=1/p DY=D[X+1]=D[X]=q/p2
25. Равномерное распределение Опр. СВНТ Х называется распределенной равномерно на [a,b], если fX(x)=0 (при x[a,b]) fX(x)=C (при x[a,b]), X~R(a,b). Найдем константу С.
C=1/(b–a).
Пример.Шкала измерительного прибора проградуированных в некоторых единицах. СВ Х – ошибка при округлении отсчета до ближайшего целого деления, то она будет иметь равномерное распределение на (-1/2 ; 1/2).Найдем mX, DX, X – ?
Решение.
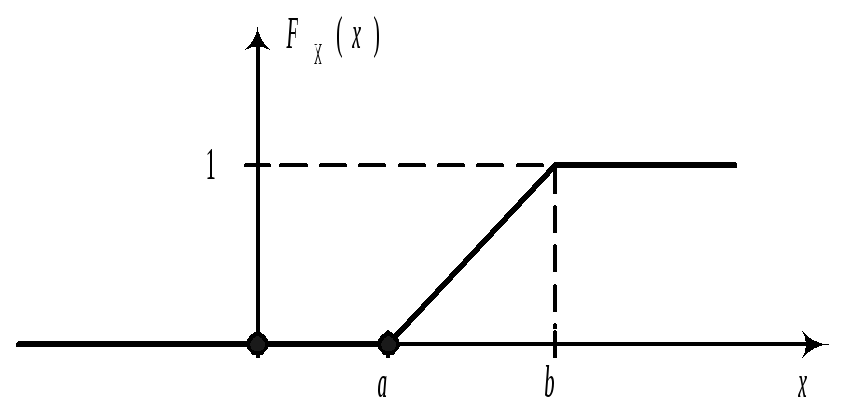
Замечание. Моды равномерное распределение не имеет, а медиана совпадает с МО. hX=mX =(a+b)/2. Найдем функцию распределения и построим ее график. FX(x)=P{X<x}
1)Случай
2)Случай
3)Случай
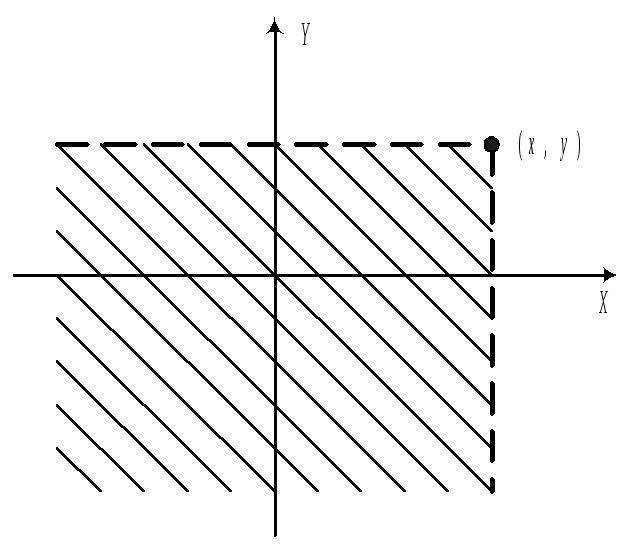
29. Совместная функция распределения
Пусть на одном
и том же вероятностном пространстве
(,A,P)
задано n
СВ,
Совместная
функция распределения:Рассмотрим
в одном и том же вероятностном
пространстве (,A,P)
набор СВ
2.
Функция
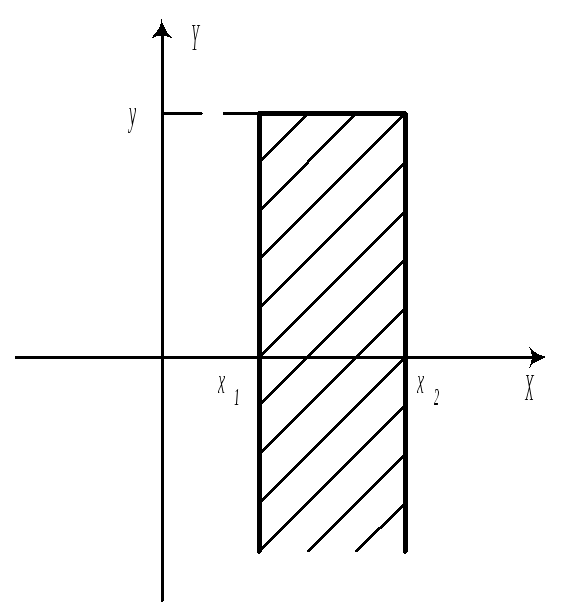
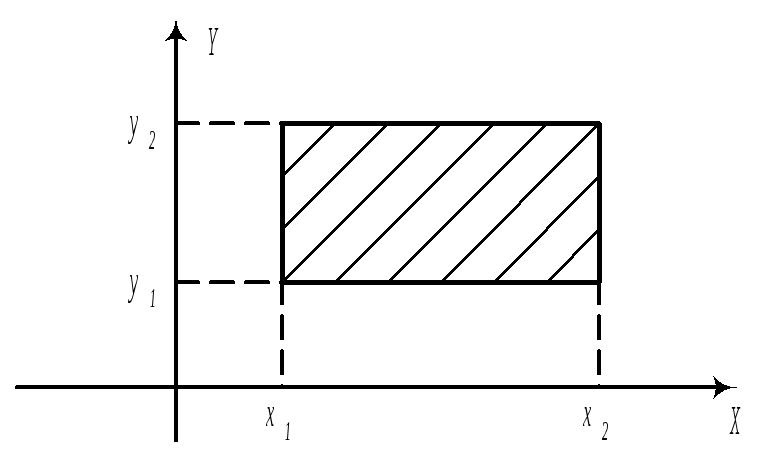
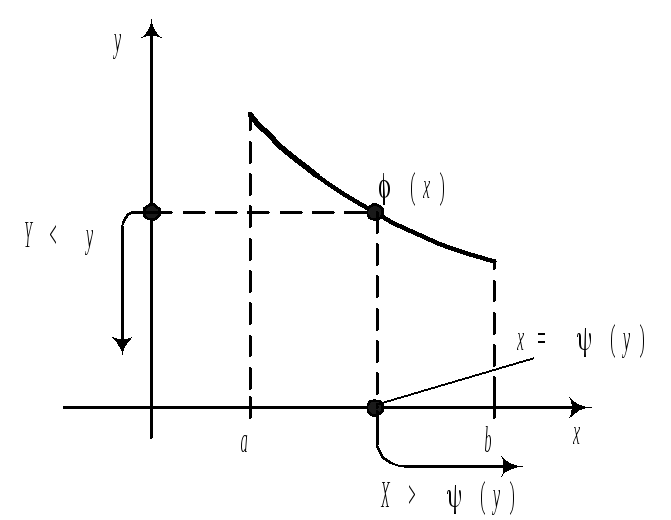
С помощью F, можно вычислить вероятность попадания случайной точки в полуполосу или в прямоугольник. а)
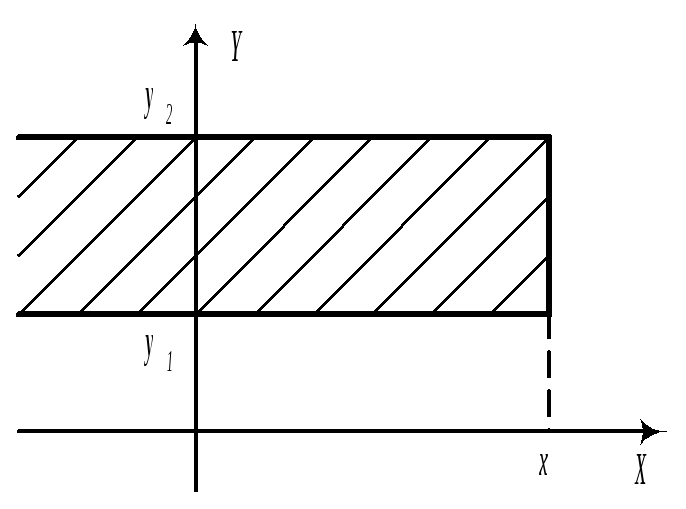
б)
в)
Свойства.
1.
2.
3.
4. а) При
б) При
34.
Мультипликативные свойства
математических ожиданий, аддитивное
свойство дисперсии
Теорема.
Если СВ X
и Y
независимы,
то M[XY]=M[X]*M[Y].
Доказательство:
Ограничимся
случаем двух дискретных СВ принимающих
конечное множество значений, тогда
В силу аддитивности МО,
Так как СВ независимы, то
Следствие:
Если СВ
Из мультипликативного СВ МО аддитивное свойство дисперсии. Теорема. Если СВ X и Y независимы, то D[X+Y]=D[X]+D[Y]. Доказательство: D[X+Y]=M[((X+Y)–(mX – mY))2]= M[((X– mX)+( Y – mY))2]= M[(X– mX)2+ 2(X– mX)( Y – mY)+ (Y – mY)2]= DX+DY+2 M[(X– mX)(Y – mY)] Так как X и Y независимы, то X– mX и Y – mY независимы D[X+Y]=DX+DY+2 M[(X– mX)(Y – mY)], где
X–
mX=MX
– mX=0
и MY
– mY=0
D[X+Y]=
DX+DY
.Следствие:
Если СВ X1,
X2
,..,Xn
– независимы, то
37.
Условное МО . Регрессия.
Опр.
Условным математическим ожиданием
одной из СВ входящих в систему (X;
Y)
называется ее МО вычисленное при
условии, что другая СВ приняла
определенное значение. Замечание.
То есть МО найденное на основе условного
закона распределения. Если СВ
Если СВ X и Y непрерывные, то
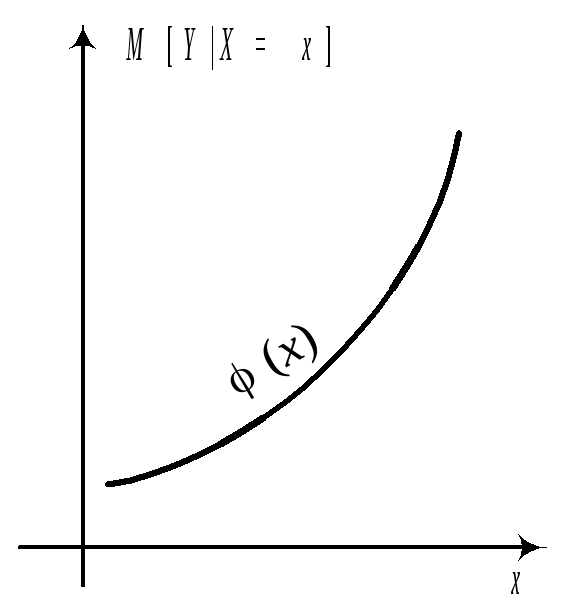
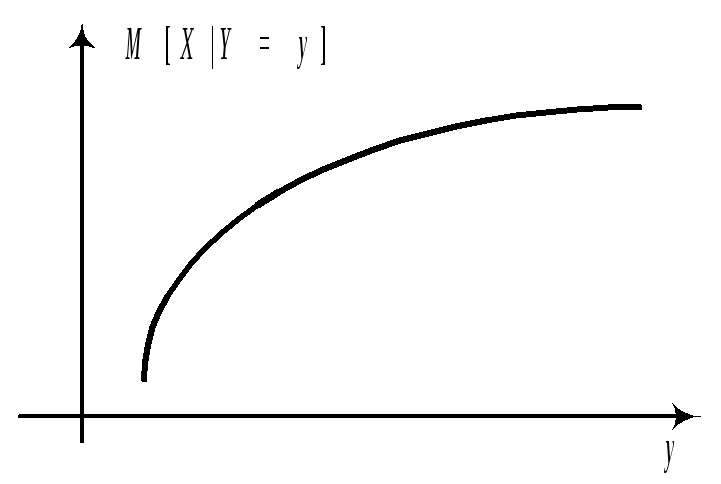
Опр M[YX=x]=(x) называется регрессией Y на x. M[XY=y]=(y) называется регрессией X на y. Графики этих зависимостей от x и от y называются линиями регрессии или кривыми регрессии.
Замечание. Для независимых СВ линии регрессии Y на x и X на y параллельны координатным осям так как МО каждой из них не зависит от того, какое значение приняла другая. Линии регрессии могут быть параллельны координатным осям и для зависимых СВ, когда МО каждой из них зависит от того, какое значение приняла другая. Так как все моменты начальные и центральные любых порядков представляют собой МО, то можно говорить об условных моментах. Например об условных дисперсиях D[YX=x], D[XY=y],.
38.Двумерные
нормальные распределения. Опр.Нормальным
законом распределения на плоскости
называется распределение вероятностей
двумерной СВ (X,
Y),
если
Итак,нормальный закон на плоскости определяется 5-ю параметрами: mX; mY; Y; Y; XY . Убедимся в том, что если компоненты X и Y не коррелированны, то они тогда и не зависимы. XY=0
Замечание: Для нормально распределенных компонент двумерной СВ понятие независимости и некоррелированности равносильны. Найдем условные законы распределения СВ X и Y воспользовавшись формулами.
Как легко видеть, каждый из условных законов распределения является также нормальных с условным МО и условной дисперсией вычисляемым по формуле:
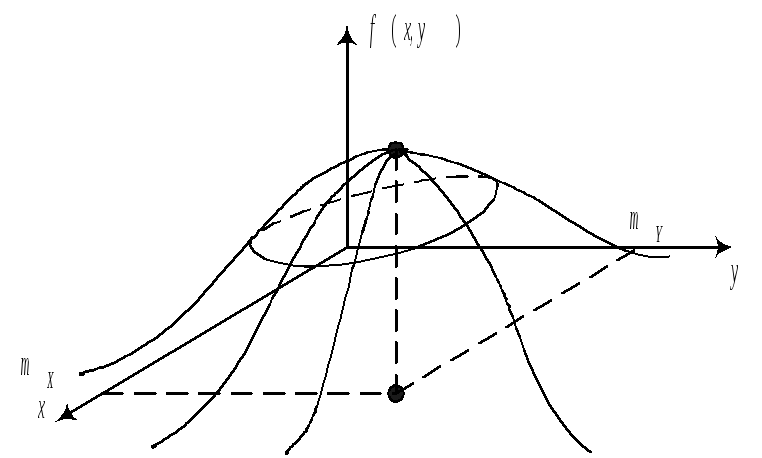
Замечание. Из двух формул для условного МО видно, что для системы нормально распределенных X и Y, линии регрессии Y на x и X на y представляют собой прямые линии, то есть регрессия всегда линейна. В геометрической интерпретации график линейной формулы плотности представляет собой холмообразную поверхность.
Сечение
поверхности
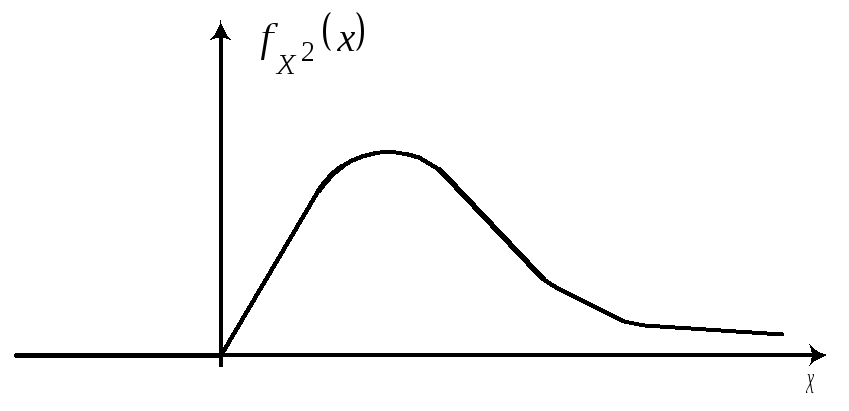
41.Распределение 2. (“хи-квадрат”).
Пусть
Zi
~N(0;1)
, i=1,2…k,
тогда
Распределение
2
определяется одним параметром числом
степеней свободы. С увеличением
степеней свободы распределение 2
медленно приближается к нормальному.
На практике при k
> 30 считают, что
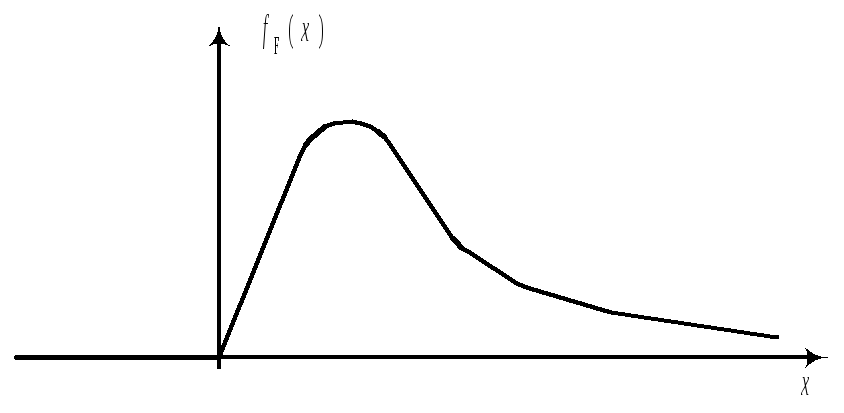
43.
Распределение Фишера.Если
U
и V
независимые СВ, распределенные по
закону 2,
44.
Неравенства Чебышева. Следующие
два неравенства называют неравенствами
Чебышева. Сформулируем их в виде
теорем. Теорема:
x>0
имеют место неравенства: Доказательство: Разложим X в сумму двух слагаемых
так как x > 0, получаем
Замечание. Очень часто второе неравенство Чебышева дают в такой форме
Второе неравенство Чебышева показывает, что при малой дисперсии с вероятностью близкой к 1 СВ Х концентрируется около своего МО.
48.Статистическое описание и вычисление оценок параметров распределения системы двух СВ. Пусть исход некоторого эксперимента описывается двумя СВ (X; Y).Предварительное представление о зависимости между X и Y можно получить, нанося элементы двумерной выборки (xi , yi ) , i=1,..,n, в виде точек на плоскость с выбранной системой координат. Такое представление называется диаграммой рассеяния. Опр. Распределением двумерной выборки называется распределение двумерного дискретного СВ случайного вектора, принимающего значения (xi,, yi) с вероятностями 1/n. Выборочные числовые характеристики вычисляются как соответствующие числовые характеристики двумерного дискретного случайного вектора. Если объем выборки небольшой, то тогда вычисления проводятся в следующей последовательности:
1.
Контроль
2. Суммы квадратов отклонений от среднего и произведения отклонений от среднего
3. 49. Линии регрессии Для СВ X и Y.
Регрессией Y
на X
называется условное МО
Если
Оценки параметров линейной регрессии по выборке (xi , yi ) , i=1,..,n можно получить, используя МНК из условия минимума суммы
Выборочная линейная регрессия Y на X. Аналогично рассматривается X на Y.
Обе прямые
регрессий пересекаются в точке с
координатами
52. Интервальные оценки. Доверительный интервал. Доверительная вероятность.
В ряде задач
требуется не только найти для параметра
Для определения
точности оценки
Для определения
надежности оценки
Опр.
Доверительным интервалом для параметра
Опр.
Число
Замечание.
Нижняя
Выбор доверительной вероятности каждый раз определяется конкретной постановкой задачи. Обычно р = 0,9; р = 0,95; р = 0,99. Часто применяют односторонние доверительные интервалы
В
простейших случаях метод построения
доверительных интервалов состоит в
следующем
Рассмотрим нахождение доверительного интервала для среднего и дисперсии нормально распределенной генеральной совокупности.
53. Доверительный интервал для оценки МО при известной дисперсии 1) Доверительный интервал для оценки МО при известной дисперсии нормально распределенной генеральной совокупности.
Пусть
Статистика
По
таблице нормального распределения
найдем квантили
Учитывая,
что
57.
Критерий
Критерий
Процедура
применения критерия
Этапы:
Если
Х–СВНТ – разбить множество значений
на r
– непересекающихся интервалов
Х–СВНТ
вычислить
e – количество оцениваемых параметров. Малочисленные частоты надо будет объединять. Проверка гипотезы о равномерном распределении генеральной совокупности. n = 200 А;
1.
2.
k = 10 – 2 – 1 = 7
|
5-6..Размещения и сочетания Набор элементов xi1, xi2, …, xin из множества X={x1,…,xn} называется выборкой объема r из n-элементов <n, r>-выборка. Выборка называется упорядоченной, если порядок следования элементов в ней задан. Замечание:Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов. Упорядоченная <n, r>-выборка, в которой элементы могут повторяться, называется<n, r>-размещением с повторениями. Упорядоченная<n, r>-выборка элементы, которой попарно различны, называется <n, r>размещением без повторений (<n, r>размещением).Замечание<n,n>-размещения без повторений называются перестановками множества X.Неупорядоченная<n,r>-выборка, в которой элементы могут повторяться, называется <n, r>-сочетанием с повторениями. Неупорядоченная <n, r>-выборка элементы, которой попарно различны, называется <n, r>-сочетанием без повторений (<n, r>-сочетанием).Замечание:Любое <n, r>-сочетание можно рассматривать, как r-элементное подмножество n-элементного множества.
Теорема
1:
Теорема
2: Доказательство:Каждое <n,r>-размещение без повторений является упорядоченной последовательностью длины r. По правилу произведения получаем
Теорема 3:
Теорема
4:
7. Геометрические
вероятности .Задача Бюффона.Геометрические
вероятности –
класс моделей вероятностных пространств,
дающий геометрические вероятности.
Пусть Ω={ω} – ограниченное множество
n-мерного
евклидова пространства с конечным
n-мерным
объёмом. Событиями назовём подмножества
Ω, для которых можно определить
n-мерный
объём. Для любого A
A
положим P(A)=A/
Ω ,
где |V|-n-мерный
объем множества V
A.Это
вероятностное пространство служит
моделью задач, в которых частица
случайно бросается в область Ω.
Предполагается, что положение частицы
равномерно распределено на множестве
Ω, т. е. вероятность попадания частицы
в подмножество A
пропорциональна n-мерному
объёму этой области. Замечание:В
классе конечных вероятностных
пространств в систему A
входили все подмножества Ω. При
геометрическом определении вероятности
в качестве A
уже нельзя
взять все подмножества Ω, так как
некоторые из них не имеют n-мерного
объёма. Примеры:
1) Стержень
разламывается на две части в случайной
точке, равномерно распределённой по
длине стержня. Найти вероятность
того, что длина меньшего обломка
окажется не больше трети длины всего
стержня.
Задача
Бюффона:Плоскость
расчерчена па-раллельными прямыми,
расстояние между которыми равно a.
На плоскость наудачу брошена игла
длины l
(l<a).
Найти
вероятность того, что игла пересечет
какую-либо прямую. Решение:. Пусть y
– расстояние от центра иглы до
ближайшей прямой (0y
a/2),
а x
– ост-рый угол, составленный иглой с
этой прямой (0x
π2).
Пара чисел (x,
y)
задаёт положение иглы с точностью до
выбора конкретной прямой.
12. Случайные величины и законы их распределения Пусть (Ω, A, P)–произвольное вероятностное пространство. Определение: Числовая функция X=X() от элементарного события называется случайной величиной (СВ), еслиxR: {X<x}={X()<x} A (*) Комментарий: Смысл определения состоит в следующем: поскольку не любое подмножество пространства Ω является событием, и все события составляют -алгебру подмножества A, то, естественно, рассматриваются только такие функции X=X(), для которых имеет смысл говорить о вероятности попадания X=X() в достаточно большие числовые множества. Свойство (*) гарантирует, что для любого X неравенство X<x есть событие, а, значит, имеет смысл говорить о его вероятности. Замечание: Если вероятностное пространство (Ω,A,P) является конечным, то случайной величиной называется любая числовая функция от элементарного события. Определение: Множество возможных значений случайных величин X называется область значений числовой функции X(). Если это множество является конечным или счетным, то случайная величина называется случайной величиной дискретного типа (СВДТ). Если это множество является несчетным, то случайная величина называется случайной величиной непрерывного типа (СВНТ). Пример 1: СВДТ. Опыт – бросание игральной кости. СВ X – число выпавших очков. Множество значений – {1, 2, 3, 4, 5, 6}.Пример 2: СВНТ. Опыт – дважды измеряется емкость конденсатора, с помощью точных приборов. СВ X – разность между результатами первого и второго измерений. Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.Если случайная величина X имеет данный закон распределения, то мы будем говорить, что она распределена по этому закону (подчинена этому закону распределения).Наиболее простую форму можно придать закону распределения СВДТ, обычно этот закон задается рядом распределений.Рядом распределений СВДТ Х называется таблица X x1 x2 ... xn P p1 p2 ... pn pi=P{X= xi }, x1<x2<…< xn<..
Так
как {X= x1
},{X= x2
},... –
попарно несовместны, и сумма этих
событий образует . С помощью этой таблицы можно найти вероятности любых событий.
Пример X 1 3 5 7 P 0,1 0,3 0,2 0,4 P{-3X4}=0,1+0,3=0,4 Часто бывает удобно иметь графическое изображение ряда распределения, так называемый многоугольник ряда распределения.
Часто удобной бывает механическая интерпретация СВДТ.
P1 +P2 +P3+P4=1 Аналитическое задание СВДТ
15. Математическое ожидание
Пусть
вероятность P
на конечном вероятностном пространстве
(,
A
, P)
определяется с помощью элементарных
вероятностей
Опр.
МО случайной величины
Замечание. В литературе математическое ожидание часто называют средним значением X. Из определения МО – вытекают следующие свойства Свойства:
1.
Доказательство:
2.
Аддитивность:
Доказательство:
Замечание. Из свойства 2 по индукции выводится свойство конечной аддитивности.
3.
Доказательство:
4.
Если
Доказательство:
По свойствам 2 и 3
5. МО СВ X выражается через ряд распределения СВ X с помощью формулы
Доказательство:
Так как СВ
Пусть
1 способ. С помощью закона распределения Y; 2 способ. С помощью формулы
Докажем формулу
для
Все дальнейшие выкладки повторяют свойство 5.
19.Биномиальное распределение Опр.СВДТ Х имеет биномиальное распределение, если ее возможные значения 0,1,2,…,m,.,n,а соответствующие вероятности pm=P{X=m}=Cnm pmqn–m m=0,1,..,n (0<p<1,q=1–p) Это распределение зависит от двух параметров: n, p. В литературе X~B(n,p). Рассмотрим условия, при которых возникает биномиальное распределение. Пусть производится n независимых опытов (испытаний), в каждом из которых событие А (“успех”) появляется с вероятностью p, СВ Х – это число успехов при n-опытах. Коментарии: Опыты называются независимыми, если вероятность какого-либо исхода каждого из них не зависит от того, какие исходы имели другие опыты. Покажем, что СВ Х имеет биномиальное распределение.B={x=m} – это количество успехов в n опытах , равно m. Событие B распадается на ряд вариантов, в каждом варианте успех достигается m раз, а неуспех n–m раз. Если успех ставим в соответствие 1. Если неуспех ставим в соответствие 0. 0,1,1,…,0,1 – всего n чисел m штук – “1” ; n–m штук – “0”. Так как опыты независимы, то каждый такой вариант имеет вероятность P=pm(1–p)n–m (по теореме умножения), а всего таких вариантов Cnm штук, причем все такие варианты несовместны, то по теореме сложения вероятностей несовместных событий следует. P(B)=P{X=m}= Cnm pm(1–p)n–m Найдем важнейшие числовые характеристики X~B(n,p). Воспользуемся производящей функцией
Возьмем производную по S.
20.Распределение Пуассона. Опр. СВДТ Х имеет распределение Пуассона, если ее возможные значения 0, 1, 2, …, m, … (счетное множество значений), а соответствующие вероятности выражаются формулой Pm=P{X=m}=(am/m!)e-a. Замечание.Закон Пуассона зависит только от a, смысл этого параметра состоит в следующем, он одновременно является МО и дисперсией СВ Х.
Рассмотрим условия, при которых возникает Пуассоновское распределение. Покажем, что оно является предельным, для биноминального распределения при n и одновременно р0, но nра (а~0,1–10). Теорема (Пуассона). Если n, р0, но npа, то фиксированного значения m, где m=0,1,…
Доказательство.
фиксированного значения m.
Комментарии:Так
как n-велико,
а вероятность p
- очень мала, то в каждом отдельном
опыте “успех” приходит редко.Поэтому
закон Пуассона в литературе называется
законом редких явлений.Пример:Завод
отправил на базу n=5000
доброкачественных изделий. Вероятность
того, что в пути изделие повредится
p=0,0002.
Найти вероятность того, что на базу
прибудут 3 негодных изделия.Решение.
n=5000.
p=0,0002.
np=1=a
26. Показательное (экспоненциальное) распределение.
Опр.
СВНТ Х
называется распределенной по
показательному (экспоненциальному)
закону с параметром >0
, если
Найдем mX, DX, X – ?
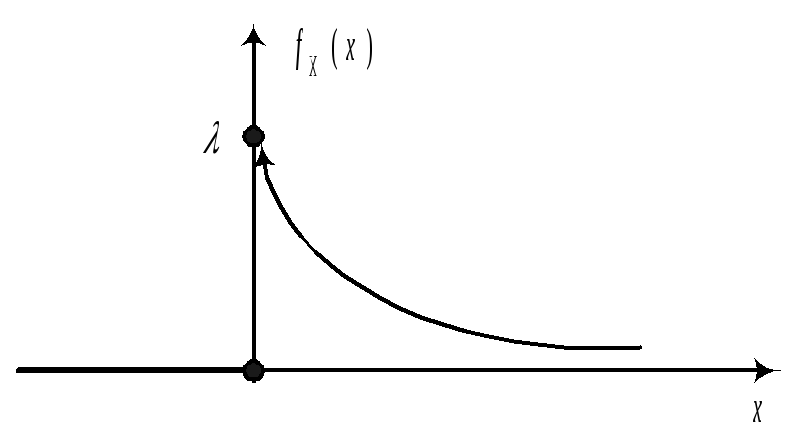
DX=1/2 X =1/ Замечание. Среднее квадратическое отклонение для экспоненциального распределения совпадает с МО. mX =X =1/ Найдем FX(x) и построим ее график
I Случай
II Случай
X =ln2/ Показательное распределение тесно связано с простейшим стационарным Пуассоновским потоком событий. Покажем, что интервал времени Т между двумя соседними событиями в простейшем потоке, имеет показательное распределение с параметром равным интенсивности потока.
Найдем
Для того, чтобы подсчитать эту вероятность нужно, чтобы хотя бы одно событие потока попало на участок длины t.
Продифференцировав
Показательное распределение играет большую роль в Марковских случайных процессах, теории массового обслуживания и теории надежности.
31.Непрерывные двумерные СВ Пусть A – -алгебра множеств двумерного пространства R2, порожденная всевозможными прямоугольниками вида
Опр.Двумерной
плотностью распределения
Из определения
Свойства.
I.
II.
III.
IV.
Опр. Двумерная СВ (X; Y) называется непрерывной, если ее распределение имеет f(x,y) Пример:(двумерное равномерное распределение)
Плотность
Замечание. По последней формуле вычисляются так называемые геометрические вероятности.
Пусть
известна
Решение.
Продифференцируем обе части равенства (*) по Х, получим
32.Зависимые и независимые СВ, В двух предыдущих параграфах было показано, как зная закон распределения системы двух (дискретных или непрерывных СВ) найти законы распределения отдельных компонент X и Y. Вопрос. Можно ли, зная законы распределения отдельных СВ (X, Y) входящих в систему , найти закон распределения всей системы? Нет, в общем виде этого сделать нельзя – это можно сделать только в одном частном случае, когда СВ X и Y образующие эту систему—независимы. Опр.Две СВ X и Y называются независимыми, если независимы все связанные с ними события {X<xi}{Y<yi}{X=xi}{Y=yi} Замечание. Так как зависимость и независимость событий всегда взаимны, то зависимость и независимость СВ, также всегда взаимна: если X не зависит от Y, то Y не зависит от X. В терминах законов распределения, независимость СВ можно определить так: две СВ называются независимыми, если закон распределения каждой из них не зависит от того какое значение приняла другая.Если компоненты X и Y двумерного вектора (X, Y) независимы, то функция распределения F(x,y) выражается, через функции распределения отдельных компонент. F(x,y)=P{X<x ,Y<y } {X<x}и {Y<y}– независимы. F(x,y)=P{X<x ,Y<y }= P{X<x}* P{Y<y }= FX(x)* FY(y) Это правило является необходимым и достаточным условием независимости для любого типа СВ.
1.
Если X
и Y
независимые дискретные СВ с матрицей
распределения
2. Непрерывные СВ.
Если СВ образующие систему зависимы, то для нахождения закона распределения системы не достаточно знать законы распределения отдельных величин, входящих в систему, требуется знать так называемый условный закон распределения одной из них.
35.Числовые характеристики системы двух СВ: Моменты начальные и центральные, ковариация. Опр.
Начальным моментом k+S
порядка системы двух СВ (X;Y)
называется K,S=M[XkYS].
Если система для двух дискретных СВ,
то
Если (X;Y) система двух непрерывных СВ, то
Опр.Центральным
моментом порядка k+S
системы двух СВ (X;Y)
называется
а) Если (X;Y) система двух дискретных СВ, то
б) Если (X;Y) система двух непрерывных СВ, то
На практике чаще всего встречаются моменты I-го и II-го порядка.
Точка с координатами
Рассмотрим
Механическая интерпретация.
Когда распределение
вероятностей на плоскости ХOY трактуется,
как распределение единичной массы
на этой плоскости, точка
Теорема:
Если СВ X
и Y
независимы, то
Доказательство:
Для независимых СВ
Замечание
Попутно
доказано, что в общем случае
Замечание.
39. Закон распределения функции одного случайного аргумента. для СВДТ:
Y=(X)
Пусть
теперь СВ X
– непрерывна и функция
Найдем закон распределения СВ Y, но при этом ограничимся случаем, когда функция (X) строго монотонна, непрерывна и дифференцируема в интервале (a, b) всех возможных значений СВ X.
1)
2)
Дифференцируя
45. Теореме Чебышева. Теорема Бернулли. ЦПТ.
Теорема
(Чебышева):Если
Доказательство:
Рассмотрим
В силу аддитивного свойства дисперсии, получаем
Следствие:
Если
Замечание. Предельные утверждения, сформулированные в теореме Чебышева и следствии к этой теореме носят название закона больших чисел (ЗБЧ). ЗБЧ утверждает, что с вероятностью приближающейся при n к 1, среднее арифметическое независимых слагаемых при определенных условиях становятся близким к константе. Из утверждения последнего следствия получаем ЗБЧ в схеме Бернулли.
Теорема
(Бернулли): Пусть
Доказательство:
Представим
Применяя следствие к теореме Чебышева, получаем утверждение к теореме Бернулли. Понятие о теореме Ляпунова. Формулировка центральной предельной теоремы (ЦПТ). Известно, что нормально распределенные СВ широко распространены на практике, объяснение дал Ляпунов (ЦПТ). Если СВ Х представляет собой сумму очень большого числа взаимно независимых СВ влияние каждой из которых на всю сумму ничтожно мало, то СВ Х имеет распределение близкое к нормальному. Приведем формулировку ЦПТ без доказательства.
Теорема(ЦПТ):Если
СВ в последовательности
где Замечание Следствиями ЦПТ являются локальная и интегральная теоремы Муавра-Лапласса.
Общее: и для 50 и для 51:
Пусть неизвестная
функция генеральной совокупности
зависит от некоторого параметра
Примеры статистик.
Эта оценка
Будет рассматриваться,
как приближенное значение параметра
Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).Требования, предъявляемые к точечным оценкам:
1. Несмещенность,
т.е.
Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной.
Иногда оценка
бывает смещенной, но асимптотически
несмещенной, т.е.
2. Состоятельность,
т.е.
Это свойство является обязательным. Несостоятельные оценки не используются. 3. Эффективность.
а) Если оценки
Если
б) Если оценки
Если
Где
Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:
50. Выборочное
среднее:
а)
Несмещенность.
По определению выборочного вектора
M[Xсред]=M[(1/n)Xi]=(1/n)M[Xi]=
(1/n)M[Xi]=(1/n)nm
D[Xсред]=D[(1/n)Xi]=(1/n2)D[Xi]= (1/n2)D[Xi]=(1/n)n2=2/n
б) Состоятельность
Воспользуемся
неравенством Чебышева:
Применим это
неравенство к
При n
55.Доверительный интервал для оценки дисперсии при неизвестном МО.
3)
Доверительный интервал для оценки
дисперсии при неизвестном МО нормально
распределенной генеральной совокупности.
Пусть
В
литературе по математической статистике
доказано, что
По
таблице распределения
58. Марковская зависимость испытаний. Определение цепи Маркова. Непосредственным обобщением схемы независимых испытаний является схема цепей Маркова. Пусть производится последовательность испытаний, в каждом из которых может осуществляться одно и только одно из k несовместных событий.
верхние индексы обозначают номер испытания.
Опр.
Последовательность испытаний образует
простую цепь Маркова, если условная
вероятность в
Пример
1. В модели
Бора атома водорода, электрон может
находиться на одной из допустимых
орбит. Обозначим, через
Разность (i–j) зависит от количества энергии, на которую изменился заряд атома в момент времени tS. Это пример цепи Маркова с бесконечным числом состояний.
59. Переходные вероятности.
Матрица
перехода.
Далее будем рассматривать только
однородные цепи Маркова, в которых
условная вероятность появления
события
Назовем
эту вероятность – вероятностью
перехода и обозначим
Полную вероятностную картину возможных изменений, осуществляющихся при переходе от одного испытания к следующему можно задать с помощью матрицы
Замечание.
Опр. Любая квадратная матрица, элементы которой удовлетворяют следующим требованиям:
Одной из главных
задач в теории цепей Маркова является
задача определения вероятности
перехода
Рассмотрим
какое-нибудь промежуточное испытание
с номером (S+m).
В этом испытании осуществится
какое-либо одно из возможных событий
По формуле полной вероятности получим
Обозначим через
Согласно формуле
(*) получаем, что
В частности, когда n = 2, получаем
n = 3
Отметим частный случай формулы (*), когда m = 1
Пример 2 Процесс блуждания с отражением.
Пусть частица,
находящаяся на прямой, движется по
этой прямой под влиянием случайных
толчков, происходящих в моменты
времени
Получается цепь Маркова с конечным числом состояний.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

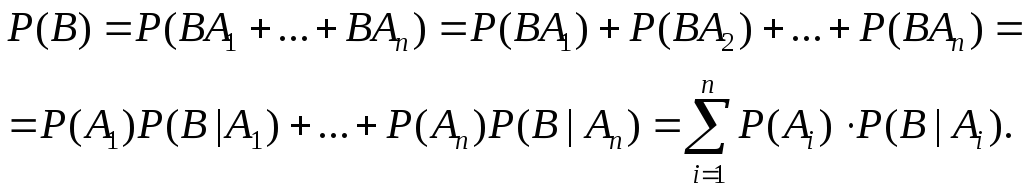
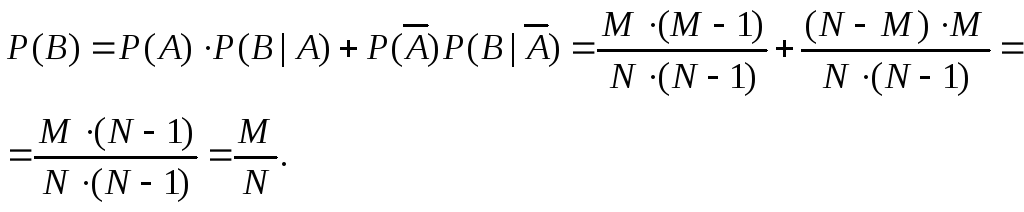
 .
.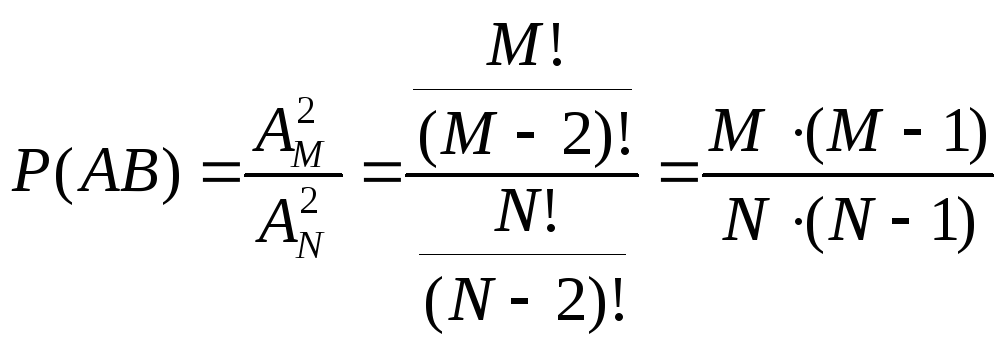 .
.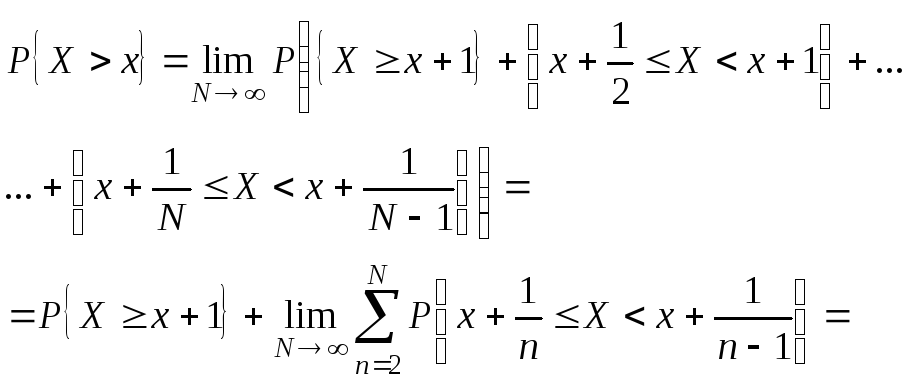 Согласно (**).
Согласно (**).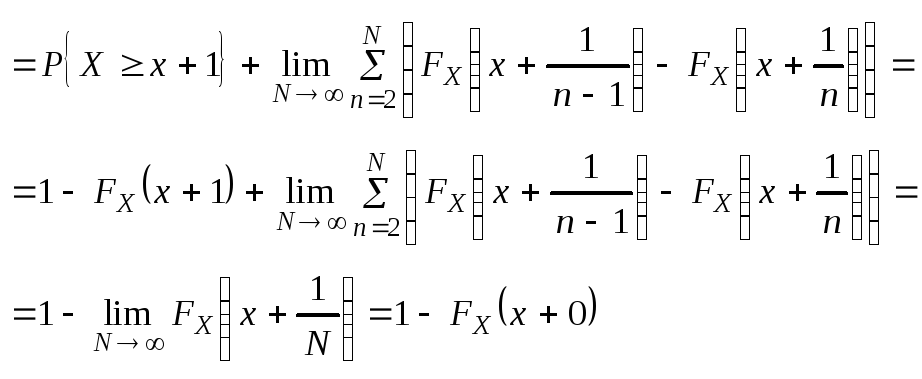
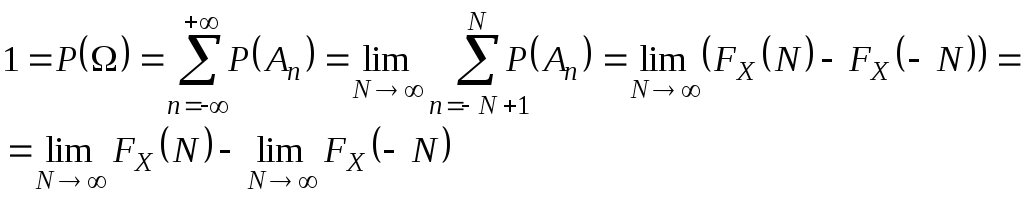
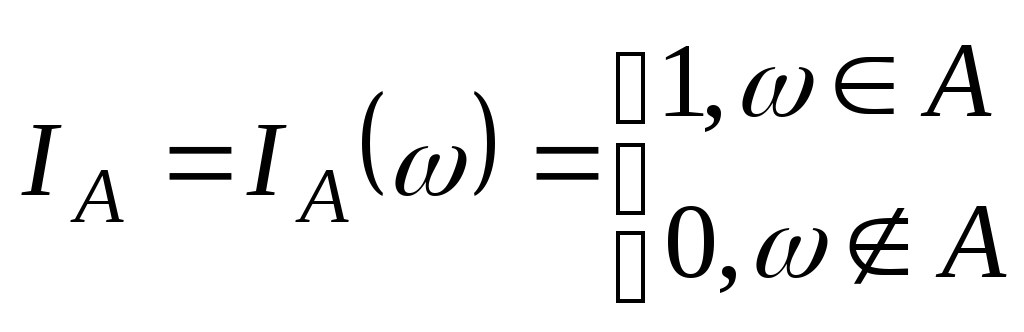 .
.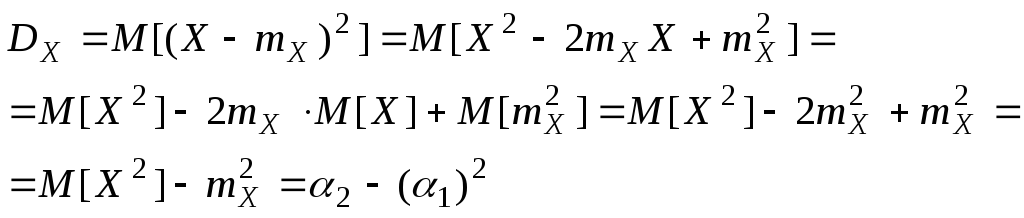 .
.

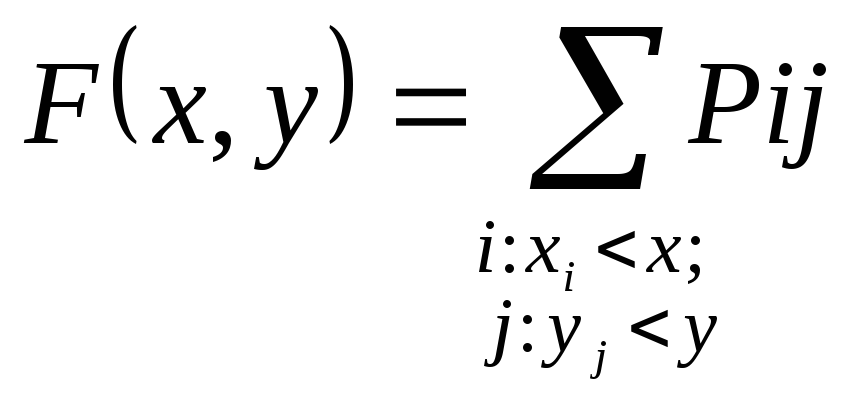
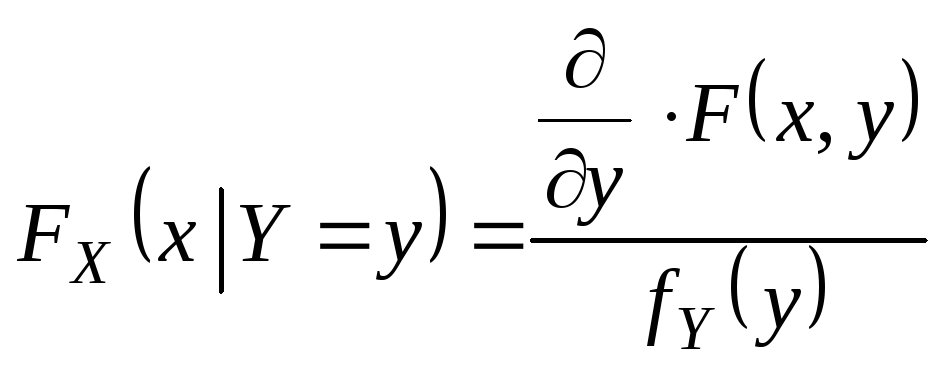
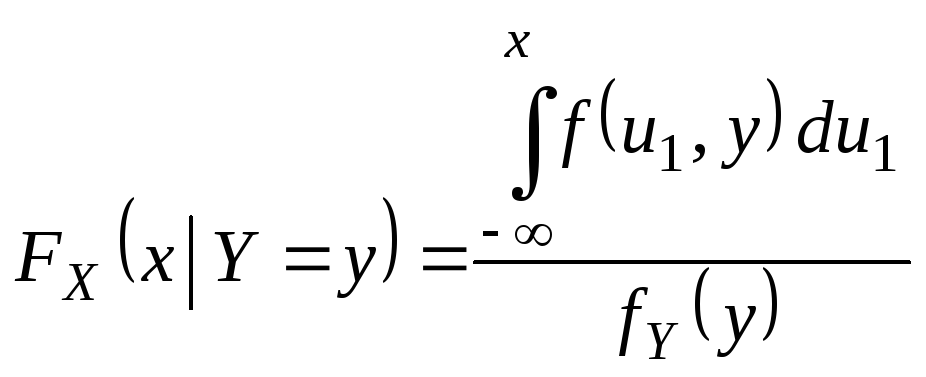
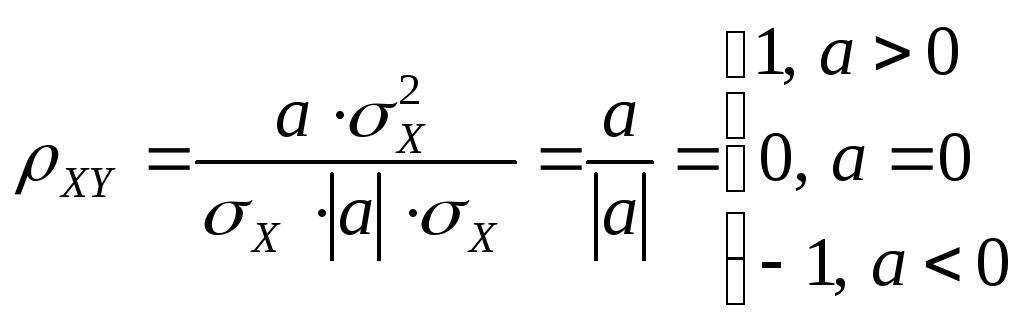
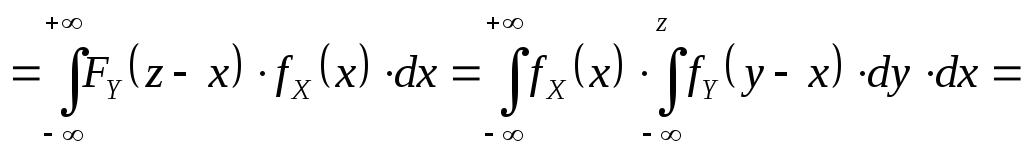
 .
.
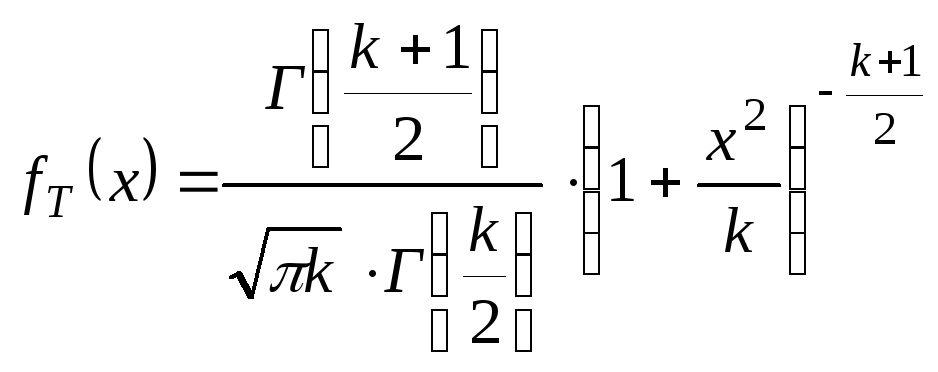
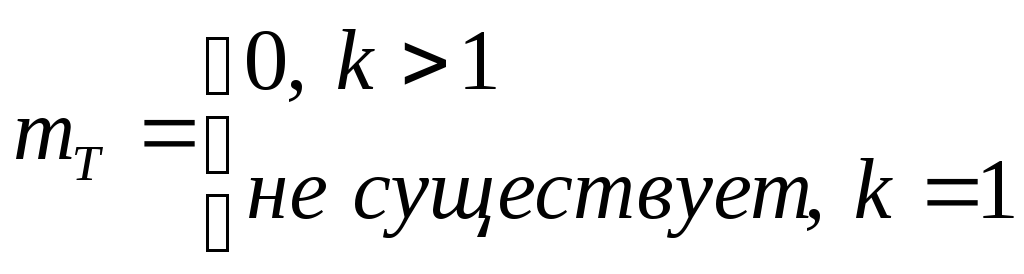
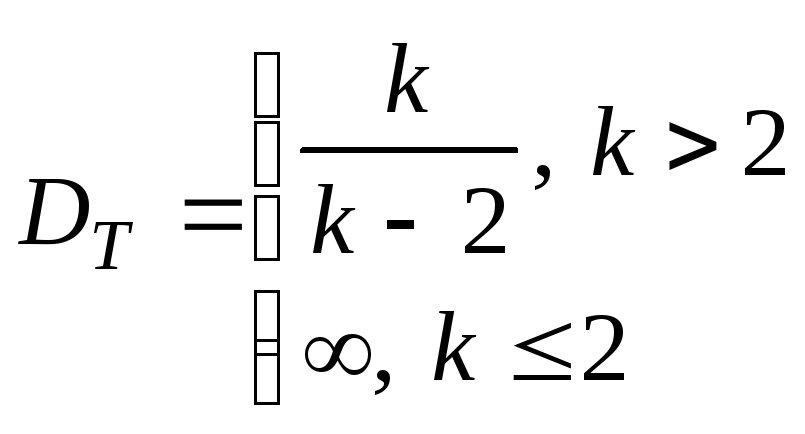
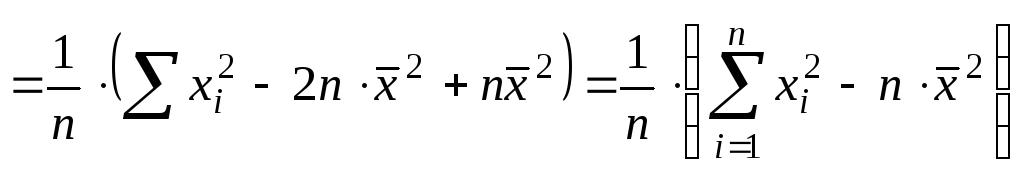
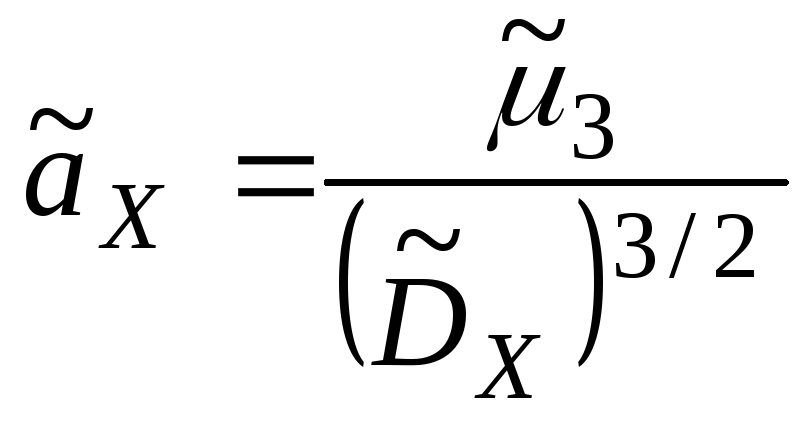
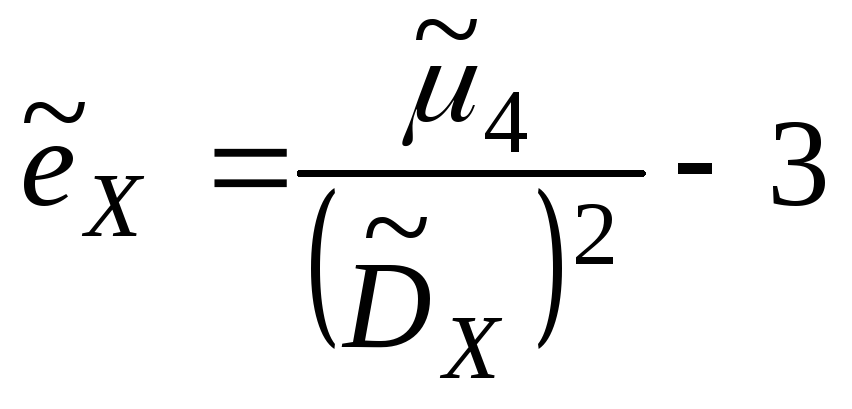
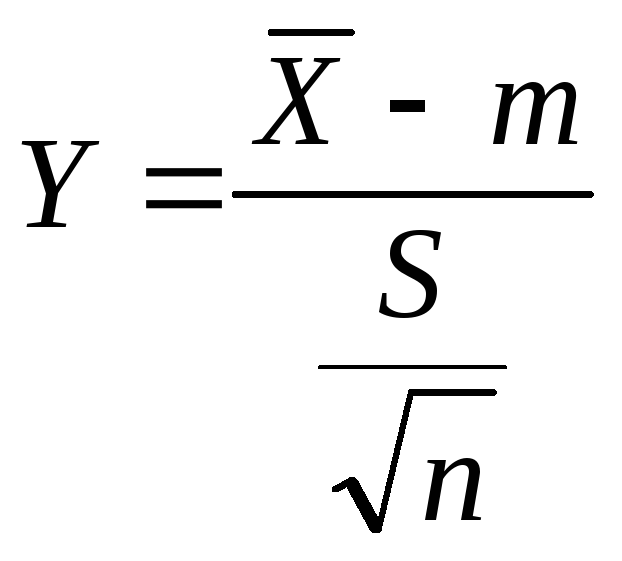 .
.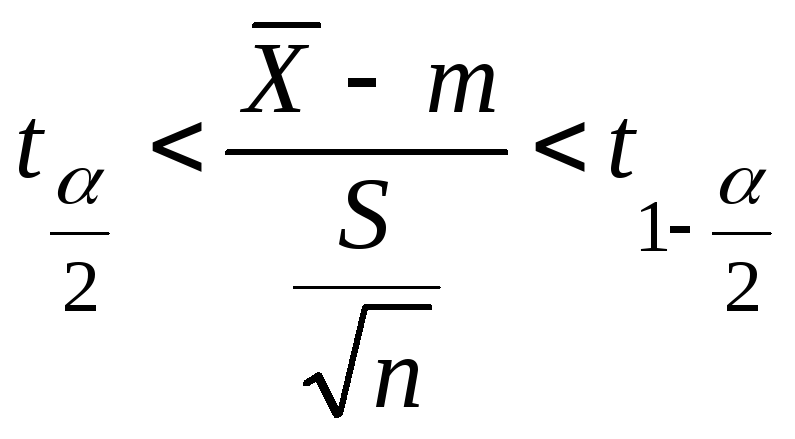 .
.

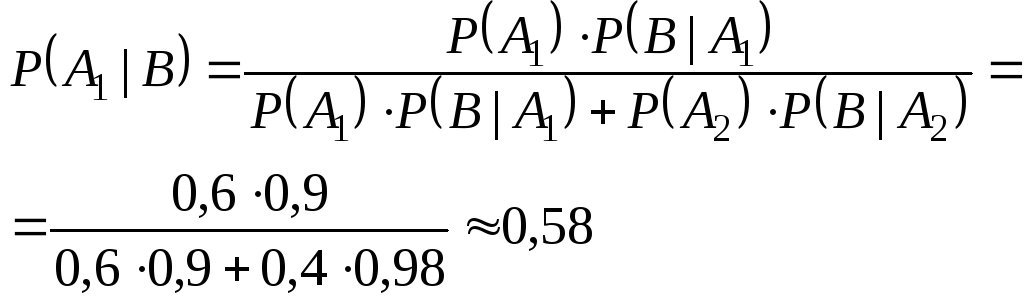
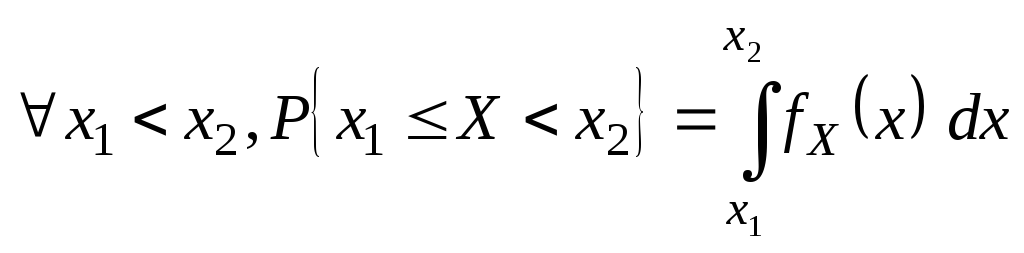 (***)
(***)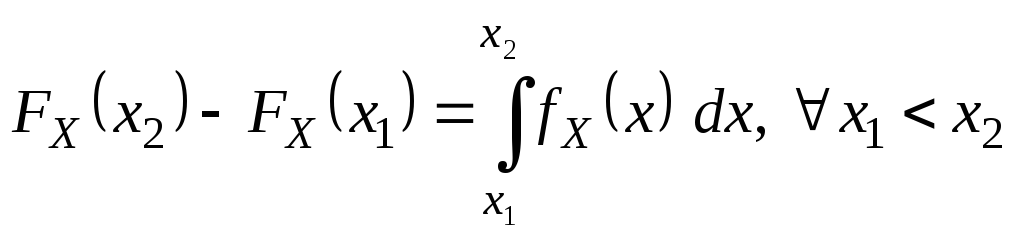 .
.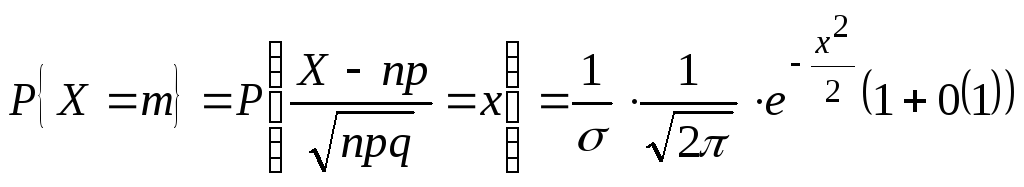
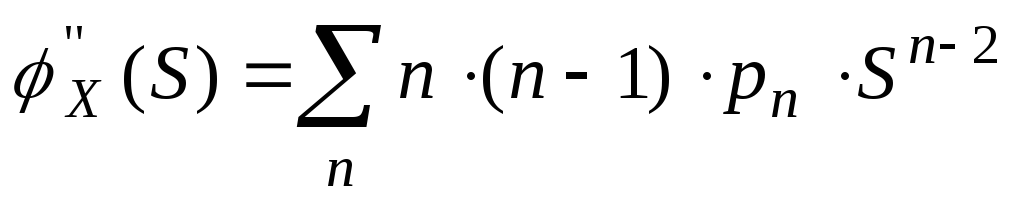

 .
.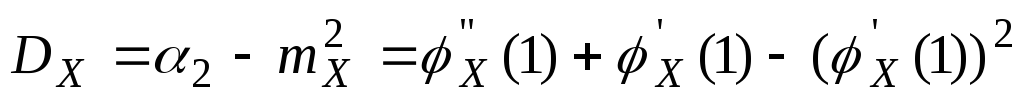 .
.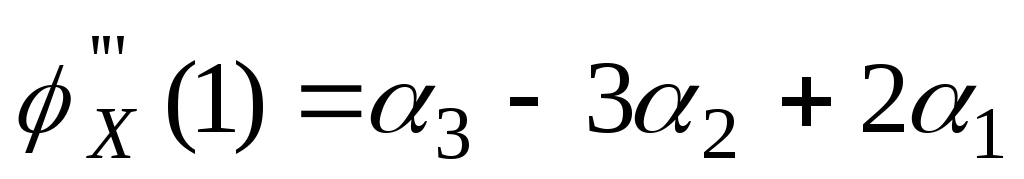 .
.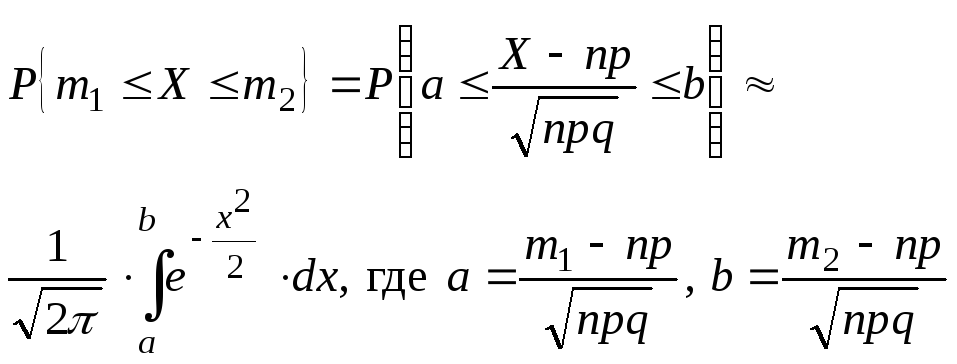
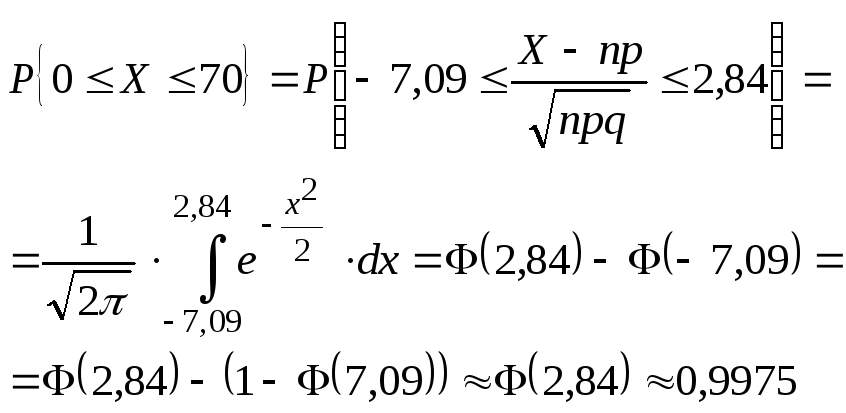
 ;
;
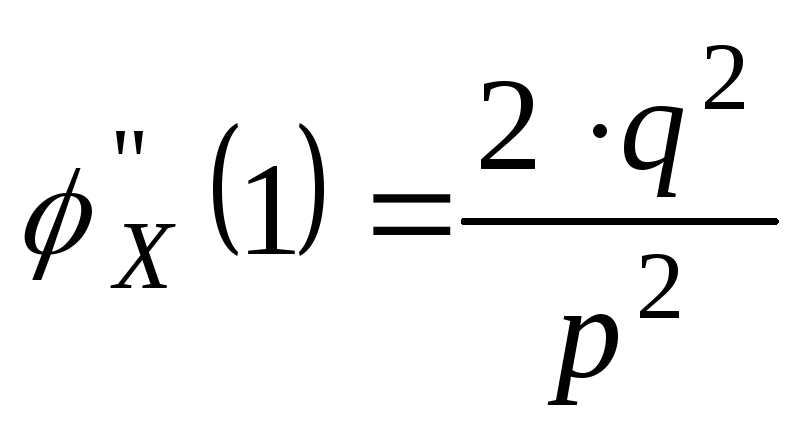
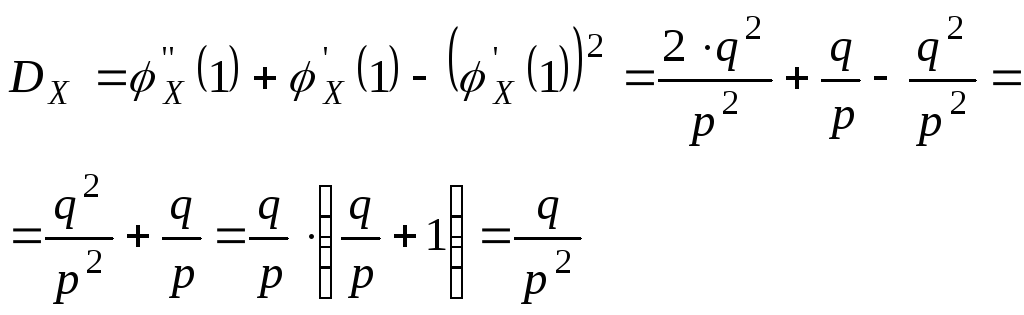
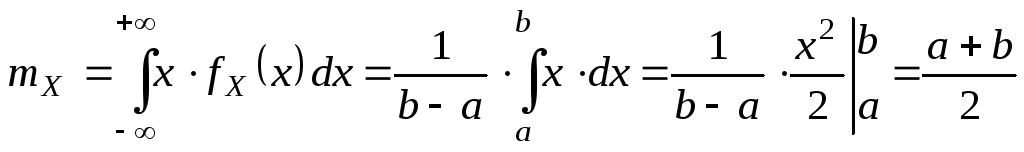

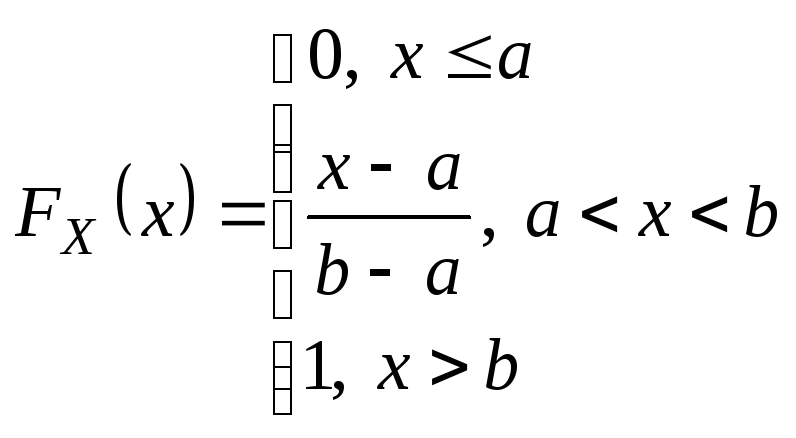
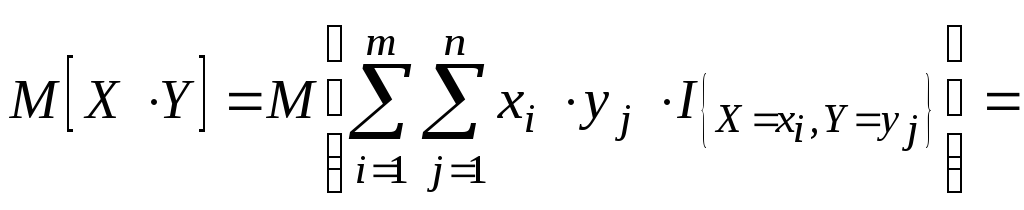
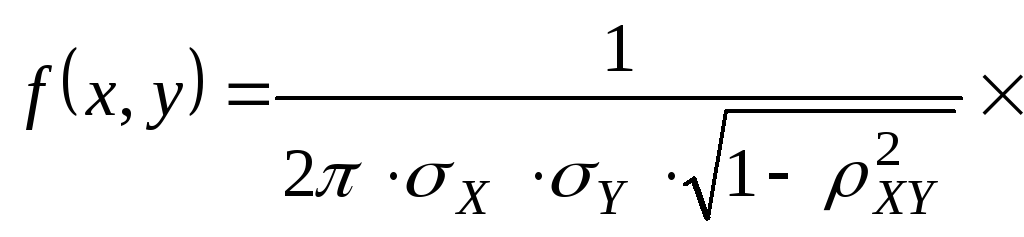
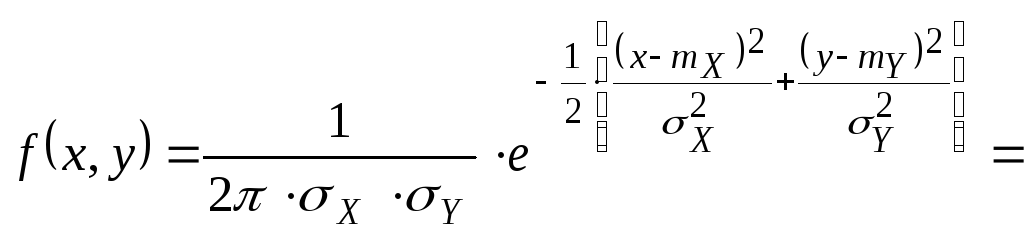
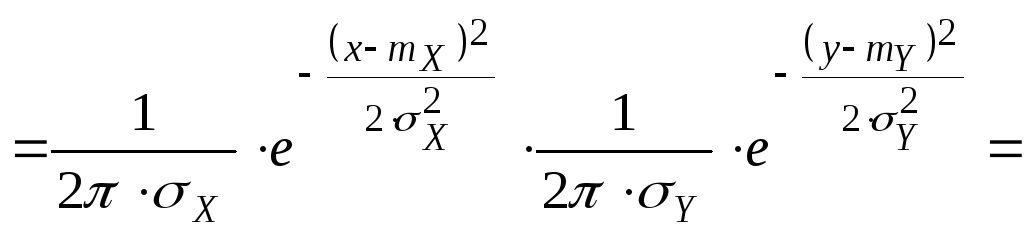
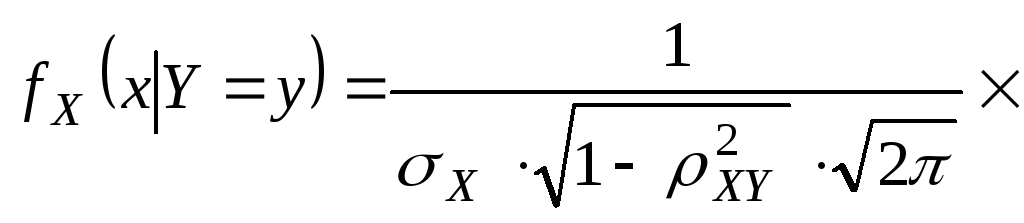


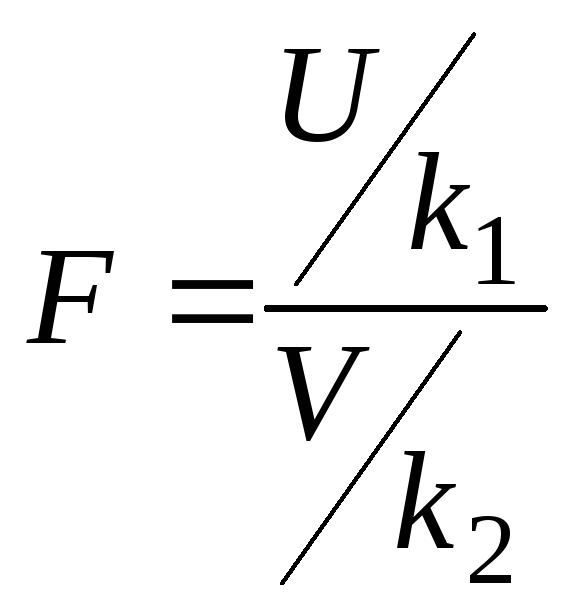 имеет распределение, которое называется
F–распределением
или распределением Фишера со степенями
свободы k1
и k2.
(
имеет распределение, которое называется
F–распределением
или распределением Фишера со степенями
свободы k1
и k2.
(
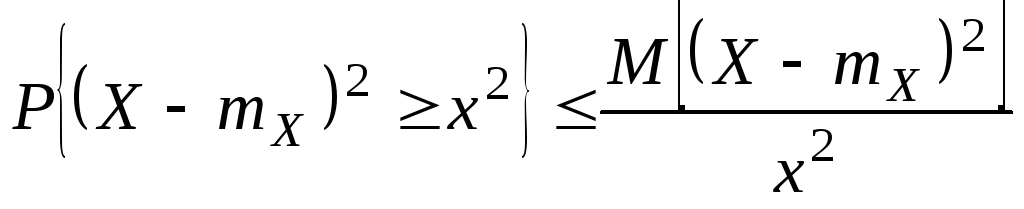
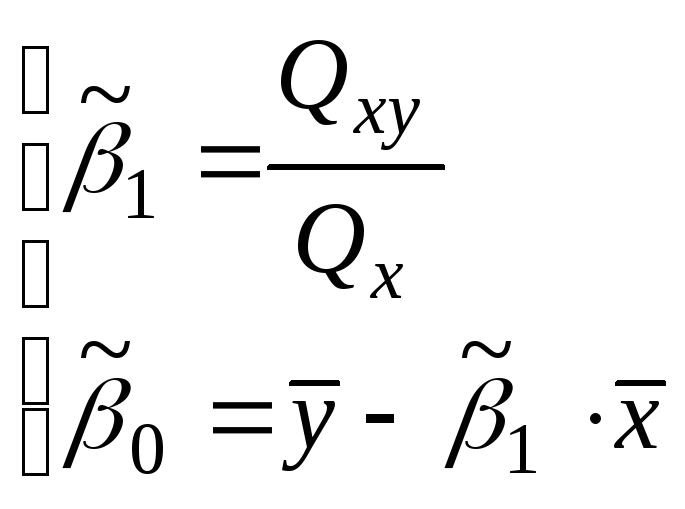 –выборочные
коэффициенты регрессии.
–выборочные
коэффициенты регрессии.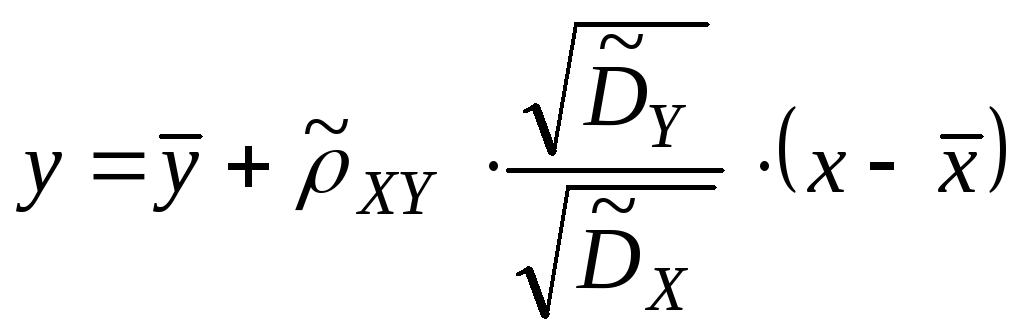 .
.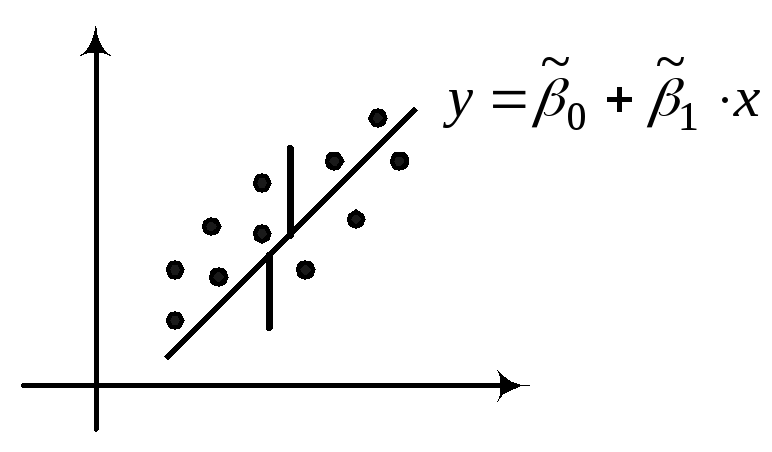
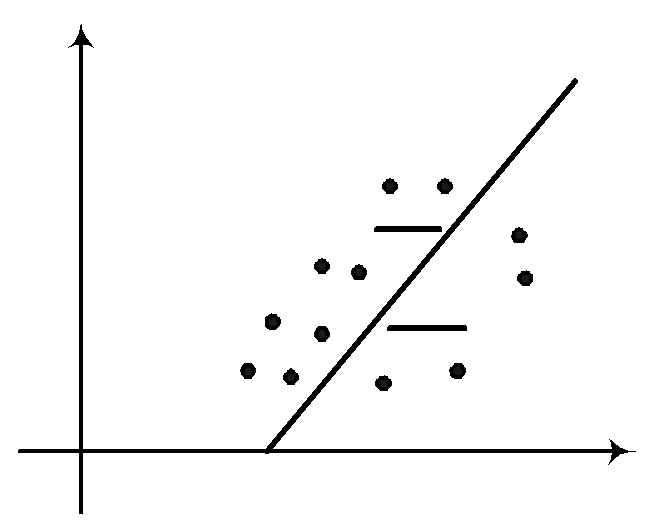
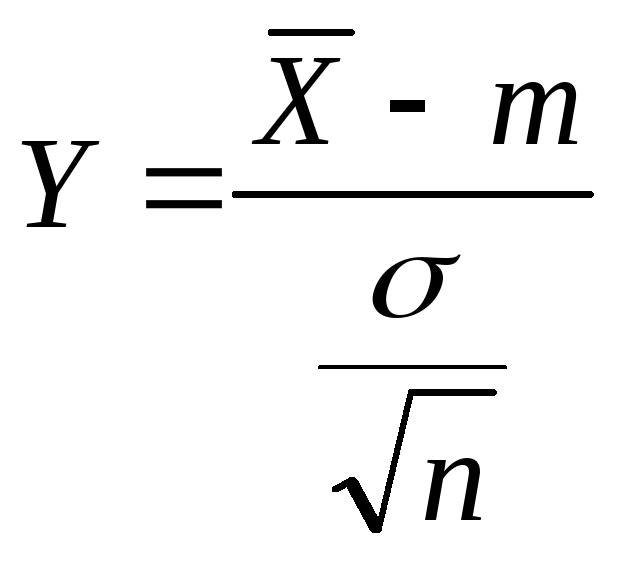 .
.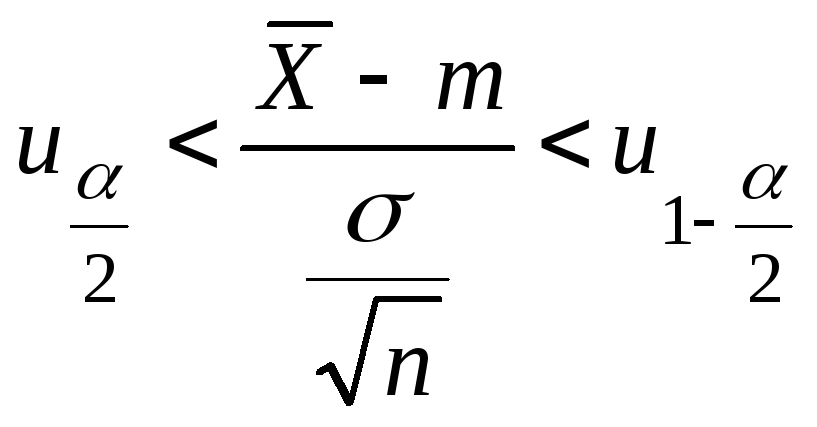 .
.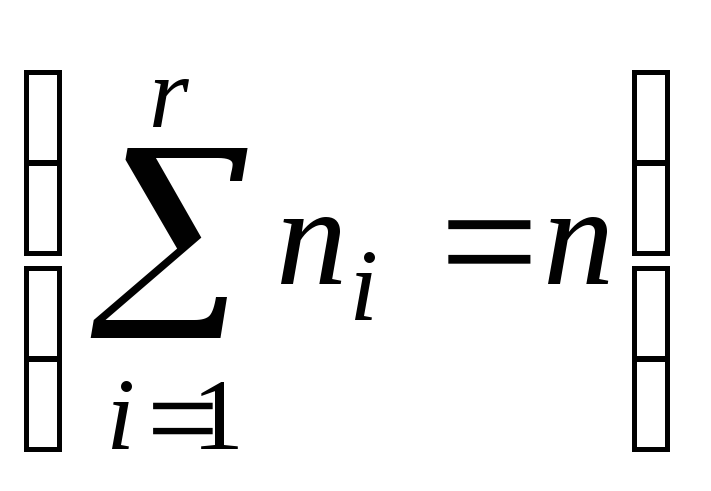 .
.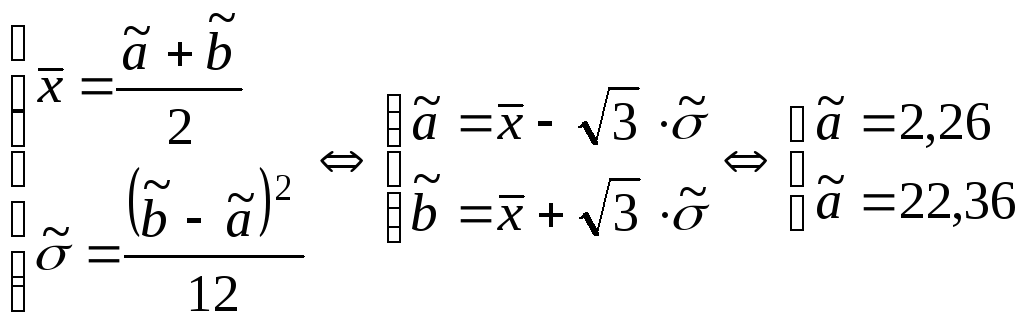
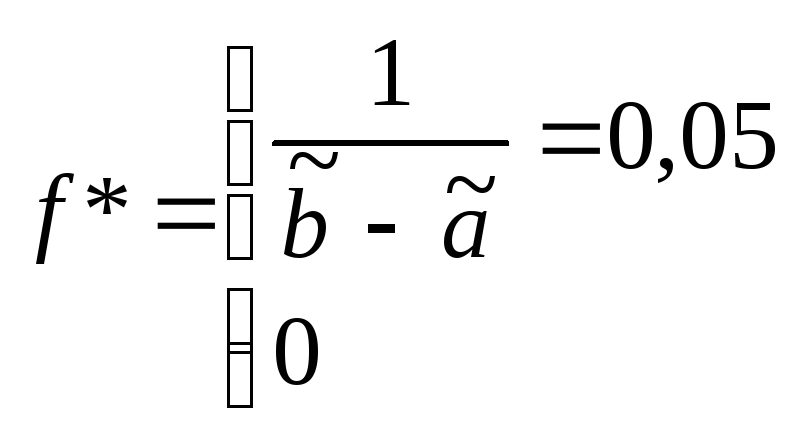
 .
.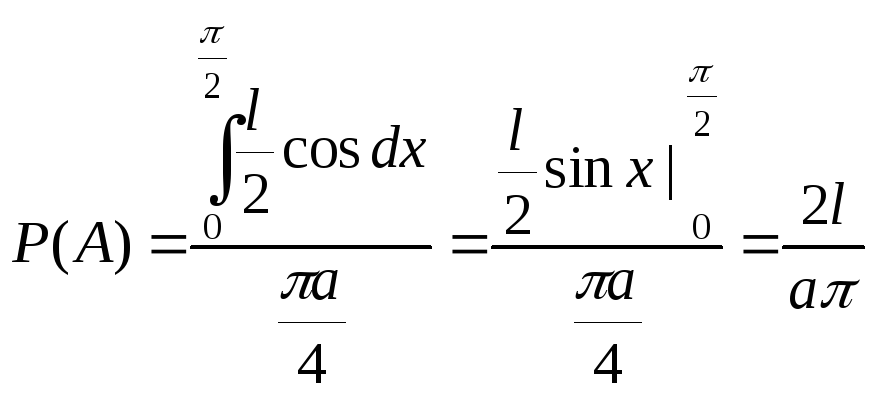
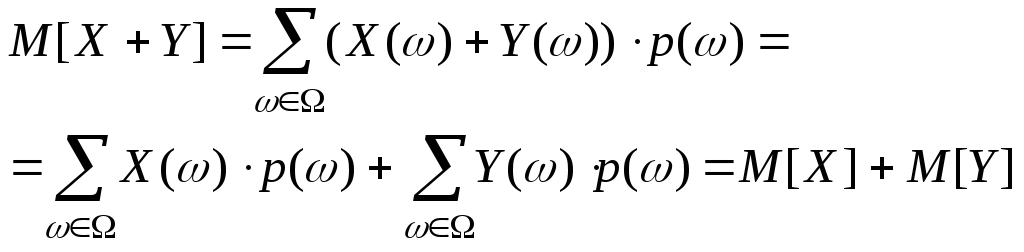
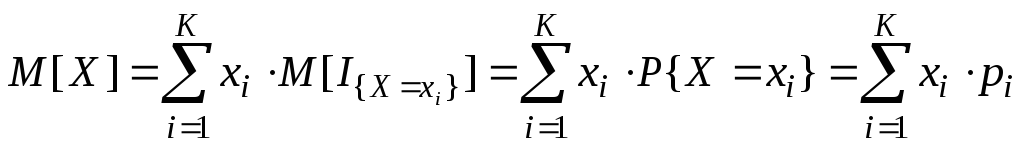 .
.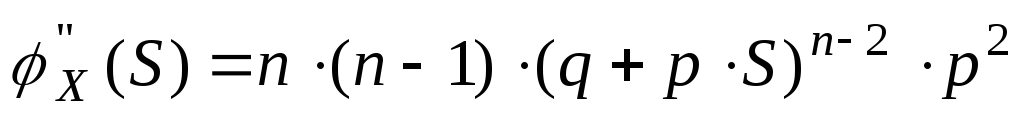
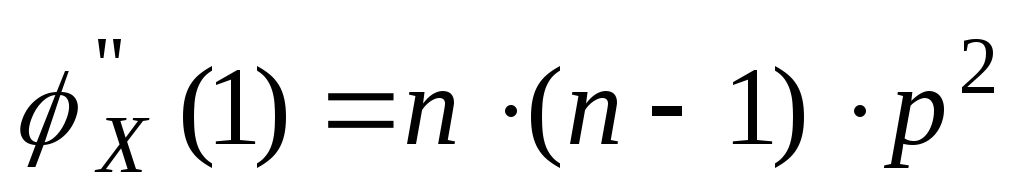
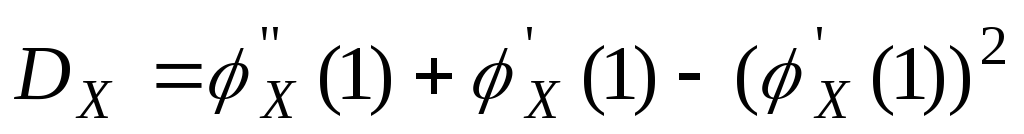
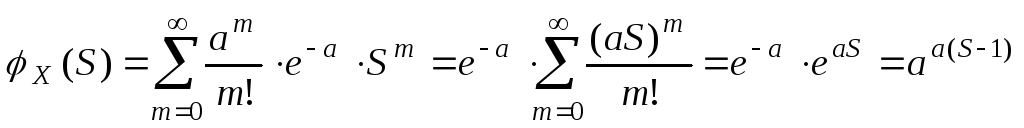
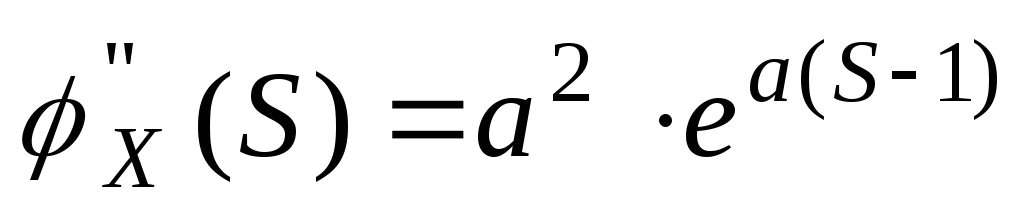 ;
DX=a2+a–
a2=a;
X=a
;
DX=a2+a–
a2=a;
X=a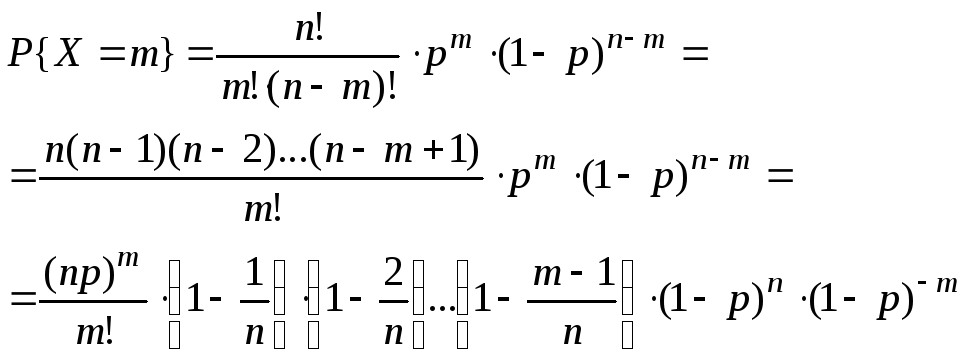
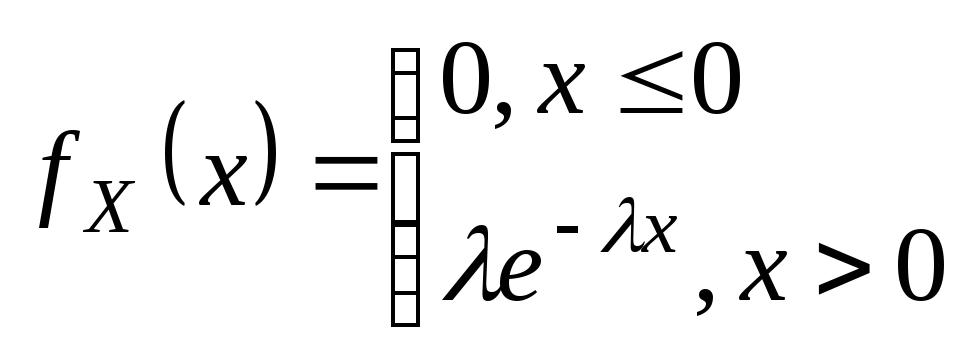 .
.
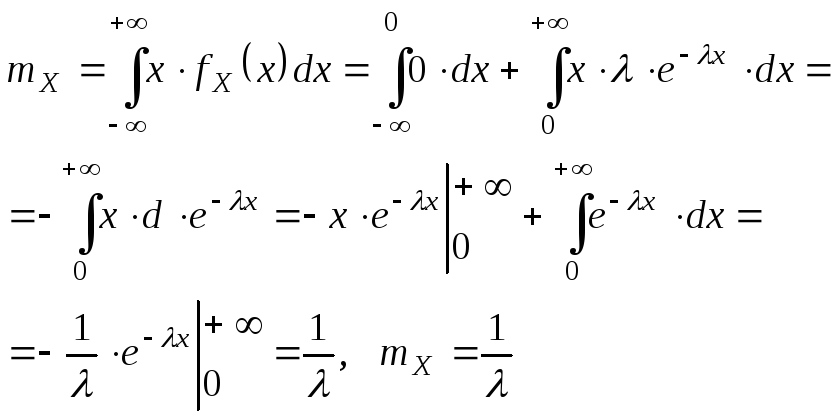
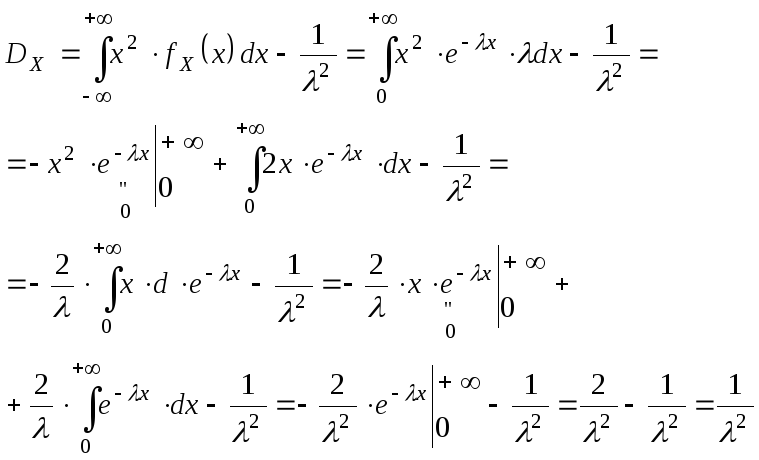
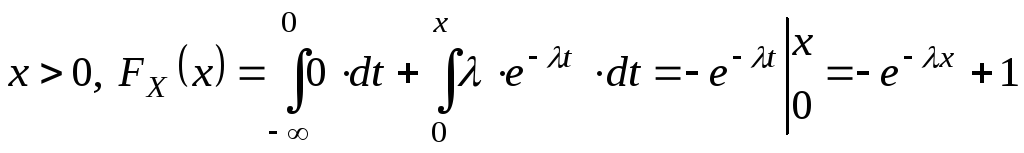
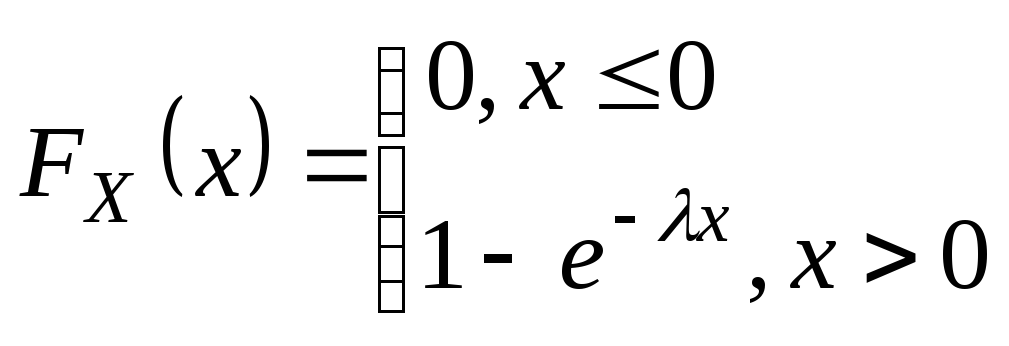
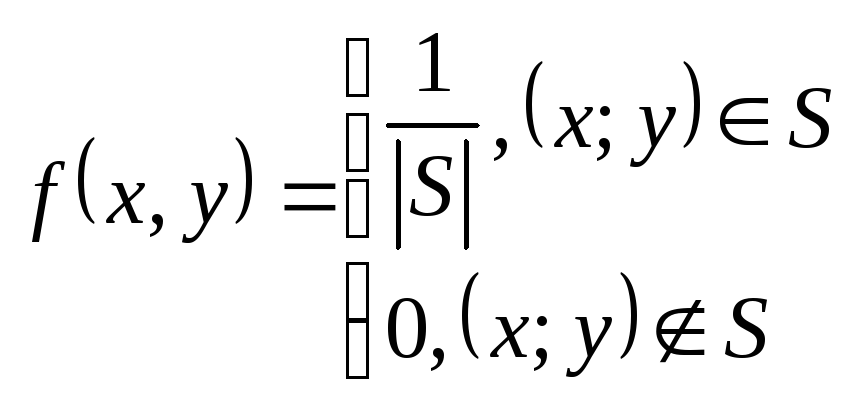

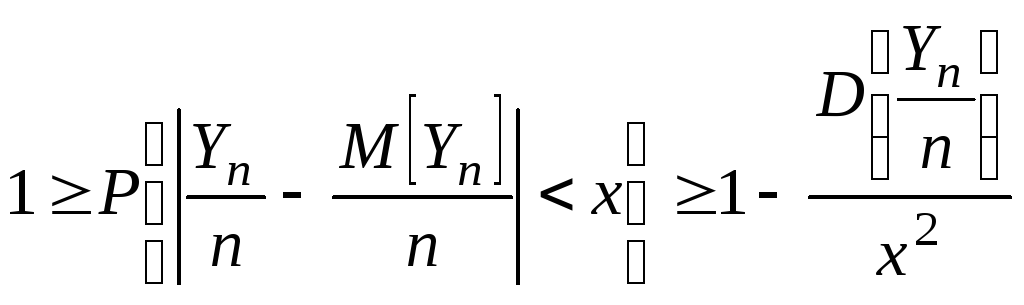 .
.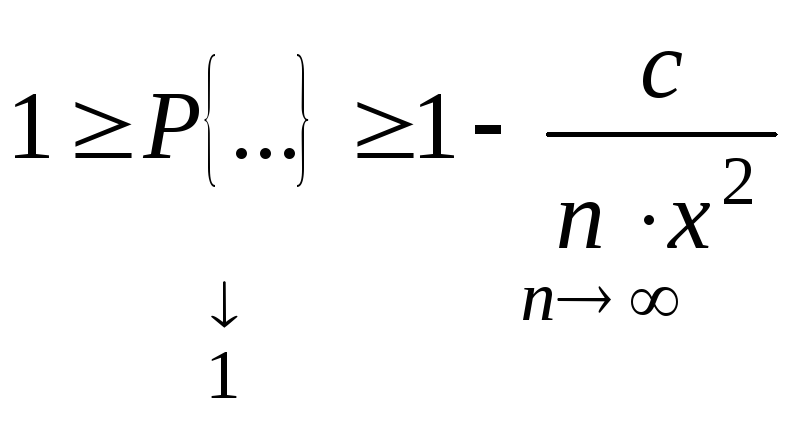
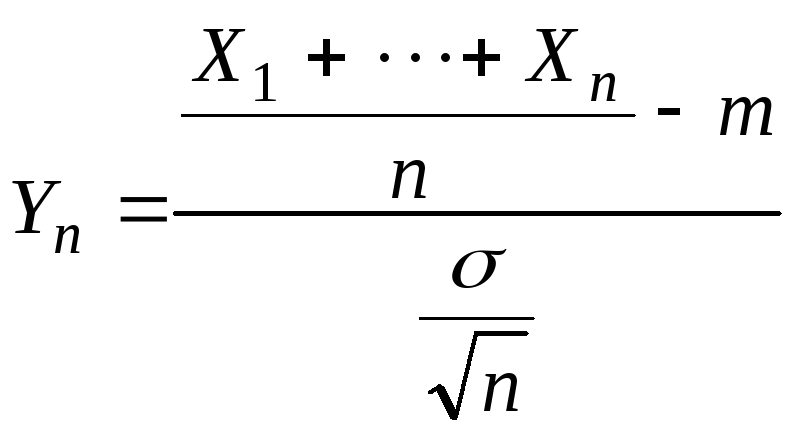 –
стандартизованное среднее арифметическое,
n-независимых
СВ в последовательности.
–
стандартизованное среднее арифметическое,
n-независимых
СВ в последовательности.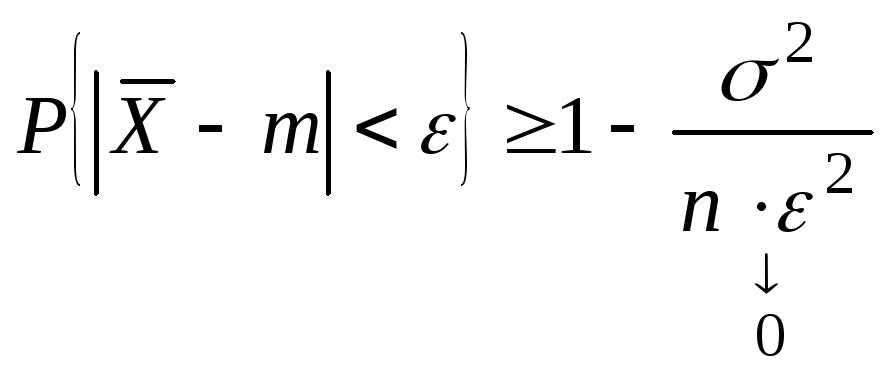
 .
.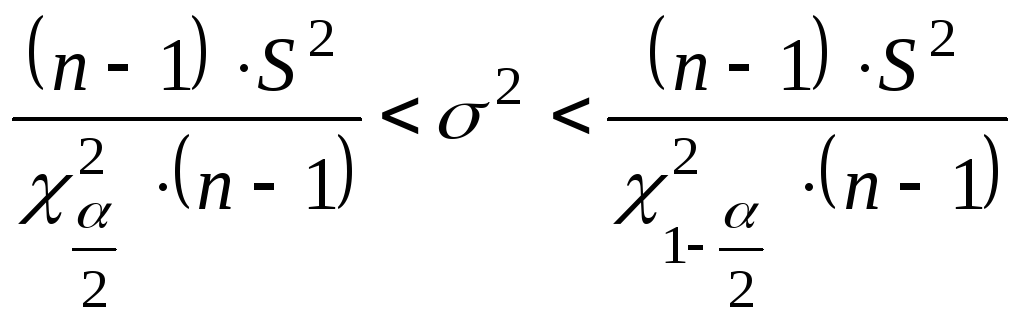 .
.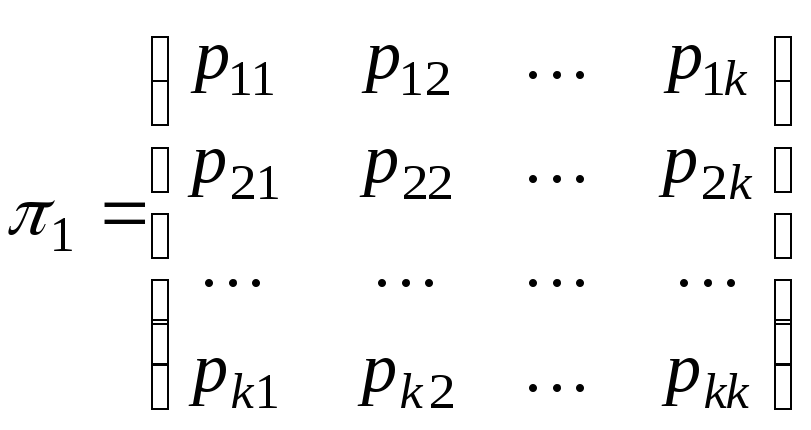 – матрица
перехода
– матрица
перехода