Лаб.раб. по механике / Лабораторная работа № 8

ЛАБОРАТОРНАЯ РАБОТА №8

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА ПРИБОРЕ ОБЕРБЕКА

ЦЕЛЬ РАБОТЫ: изучить закон вращательного движения твердого тела вокруг неподвижной оси.

ОБОРУДОВАНИЕ: экспериментальная установка, набор тел, электронный секундомер, источник питания

КРАТКАЯ ТЕОРИЯ

Вращательное движение материальной точки (МТ), как и всякое другое движение, можно описывать теми же физическими величинами и теми же кинематическими и динамическими соотношениями между ними, что и для прямолинейного и произвольного криволинейного движения. Однако для вращательного движения оказалось удобно ввести специальные «вращательные» физические величины и объединяющие их кинематические и динамические законы, которые можно вывести, а можно просто написать по аналогии.

Итак, рассмотрим сначала движение по окружности простейшего материального объекта – материальной точки (МТ).

1. Положение МТ на окружности определим углом , который образует радиус-вектор МТ с некоторым неподвижным радиусом ОА. Угол всегда измеряется в радианах. Зависимость - это кинематическое уравнение вращения МТ по окружности (аналог этому уравнению в криволинейном движении).

2. Физическая величина, определяемая соотношением

, (8.1)

называется угловой скоростью МТ (точнее ее радиус-вектора). Здесь - физически малое приращение угла поворота за промежуток времени . Единица измерения угловой скорости - 1 (аналог ).

3. Физическая величина, определяемая соотношением

, (8.2)

называется угловым ускорением. Здесь - физически малое приращение угловой скорости за промежуток времени . Единица измерения углового ускорения - 1 (аналог - ускорение ). Угловая скорость и угловое ускорение – векторные величины. Вектор (скользящий) расположен по оси вращения, а его направление связано с движением МТ правилом правого винта. Вектор (также скользящий) расположен вдоль оси вращения и ↑↑ при ускоренном движении и ↑↓ - при замедленном (при ускоренном прямолинейном движении ↑↑ и при замедленном ↑↓).

4. Физическая величина, определяемая соотношением , называется моментом инерции МТ относительно оси вращения. Здесь 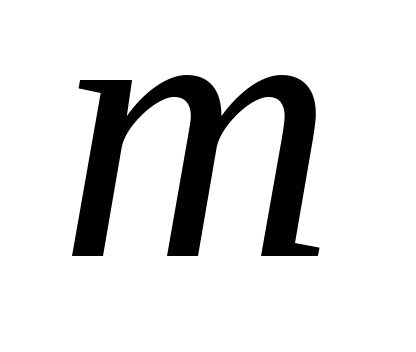– масса МТ, – расстояние от МТ до оси вращения (аналог – масса МТ). Момент инерции системы МТ естественно определить соотношением

(8.3)

здесь i=1, 2, 3… - номер МТ (аналог – масса ). Для твердого тела, где расстояние между отдельными МТ в процессе движения не меняются, формула (8.3) приобретает более простой и удобный вид. Так, например, момент инерции сплошного диска (цилиндра) равен . Здесь – масса диска, – его радиус.

5. Моментом силы , действующей на МТ, относительно точки О называется физическая векторная величина, определяемая соотношением

(8.4)

Вектор (скользящий) расположен вдоль оси вращения, а его направление определяется по правилу правого винта (или с конца вектора кратчайший поворот от вектора к вектору виден против часовой стрелки). Модуль вектора равен

(8.5)

Здесь – плечо силы относительно оси вращения. Если (сила проходит через ось вращения), то .

Проекция вектора на координатные оси называется моментом сил относительно соответствующей оси координат. На рис.8.1 , .

Если на МТ действует несколько сил (рис.8.2), то их моменты могут быть направлены в противоположные стороны, а их проекции на ось вращения будут положительными или отрицательными. Для рис.8.2 ; , так что (аналог вектора - вектор силы ).

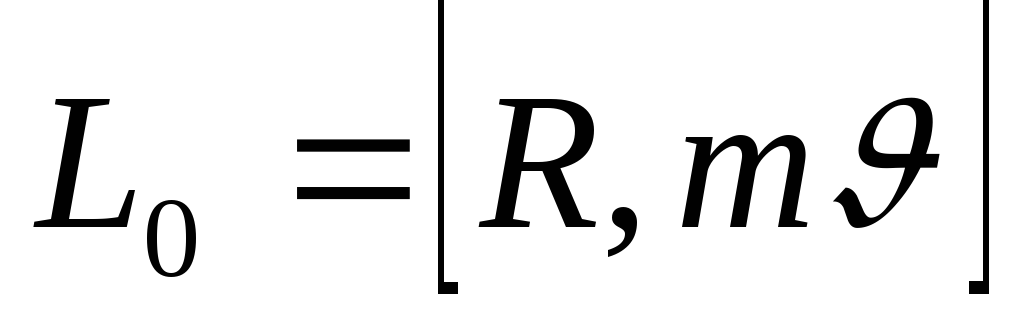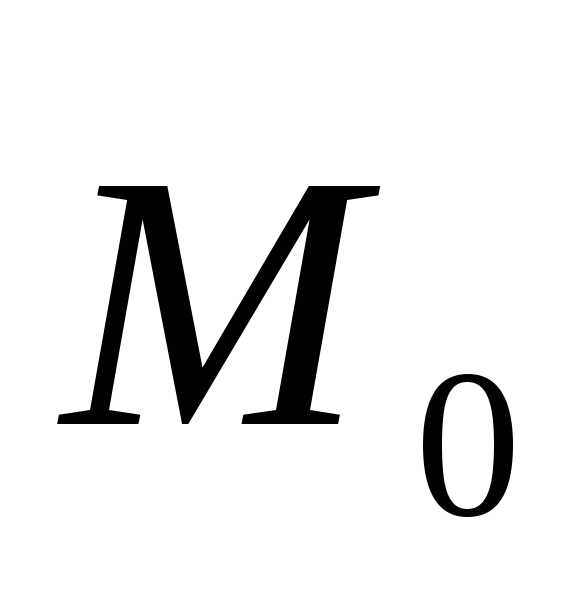6. Моментом импульса МТ относительно точки О называется векторная физическая величина, определяемая соотношением . Направление вектора определяется точно также, как и вектора . Модуль вектора равен

(8.5).

Момент импульса системы материальных точек, естественно, равен . Модуль этого вектора равен . Здесь - момент инерции системы материальных точек, угловая скорость для всех точек одинакова, поэтому у нее нет индекса суммирования (аналогом вектора является вектор ).

7. УРАВНЕНИЕ ВТОРОГО ЗАКОНА НЬЮТОНА ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА.

Уравнение второго закона Ньютона для прямолинейного и криволинейного движения МТ имеет вид или в проекциях на оси координат и . По аналогии для вращательного движения МТ можно написать или в проекциях на ось вращения

(8.6)

Такое же выражение будет иметь и уравнение второго закона Ньютона для вращательного движения твердого тела. Только под надо понимать момент инерции твердого тела, а под - сумму моментов внешних сил, действующих на тело, относительно оси вращения.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. ТЕОРИЯ МЕТОДА И МЕТОДИКА ИЗМЕРЕНИЙ

Экспериментальная установка представляет собой один из вариантов прибора Обербека. На сплошном диске, который может с малым трением вращаться вокруг горизонтальной оси, установлены два шкива радиусами и Вращение диска осуществляется силой натяжения нити, намотанной на один из шкивов.

Прикрепляя к нити различные грузы, можно изменять момент силы натяжения и, следовательно, угловое ускорение диска. Электрическая схема установки позволяет включать секундомер одновременно с началом вращения диска и автоматически отключать его при прохождении грузом определенного расстояния . На другой стороне диска имеются приспособления для установки двух () цилиндров на различных расстояниях и от оси вращения диска.

Напишем уравнение второго закона Ньютона для опускающегося груза и вращающегося диска с цилиндрами (или без них).

а) или . Отсюда получаем

(8.7)

Ускорение найдем из соотношения , здесь h – путь,

проходимый грузом массой m за время t. Следовательно,

(8.7а)

б) . Здесь

; (8.8)

С помощью соотношений (8.7а) и (8.8) получаем

(8.9)

– момент инерции диска с цилиндрами или без них.

1) ПРОВЕРКА УРАВНЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ (формула 8.6). Из этого уравнения следует условие: при неизменном моменте инерции прибора . Здесь , … - моменты сил натяжения, создаваемые падающими грузами различной массы, а , … - соответствующие им угловые ускорения. Однако удобнее проверять не это уравнение, а следствие из (8.6) – уравнение (8.9). Из него следует, что при неизменных значениях момента инерции диска, массы падающего груза и радиуса шкива r правая часть будет постоянной для различных наборов h и t. Таким образом, задавая значения h₁, h₂, h₃… и измеряя время падения t₁, t₂, t₃… (не менее трех раз для каждого h), можно убедиться в выполнимости условия

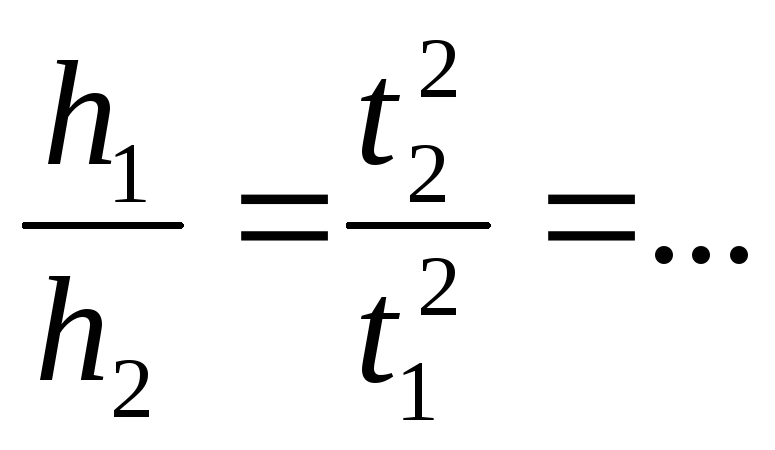
2) ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ. Измерим время падения t₂ груза массой m для диска с цилиндрами, установленными на расстоянии d₁ и время t₃ – для диска с цилиндрами на расстоянии d₂. Получим:

(8.10)

(8.11)

(8.12)

Каждое время находим как среднее из пяти измерений. Используя соотношение и формулы (8.10 - 8.12), получим

(8.13)

(8.14)

Таким же способом можно измерить и моменты инерции любых других тел, которые можно укрепить на диске.

3) ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА. При перемещении цилиндров на диске с расстояния d₁ на расстояние d₂ их момент инерции увеличивается. Это приращение момента инерции можно подсчитать двумя независимыми способами. Из формул (8.13) и (8.14) следует

(8.15)

С другой стороны, по теореме Штейнера имеем:

; (8.16)

Если теорема Штейнера верна, то значения , вычисленные по формулам (8.15) и (8.16) в пределах погрешностей должны совпадать.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

а) Для нахождения моментов инерции тел и с помощью формулы (8.15) необходимо измерить время падения груза - , , , следовательно, вращения диска без тел () и с телами (, ), укрепленными на расстояниях и .

б) Подсчитать разность полученных значений моментов инерции и сравнить с разностью, даваемой формулой (8.16). Сделать заключение о выполнимости теоремы Штейнера.

в) Найти угловые ускорения и вращения диска (с телами или без тел) под действием моментов силы натяжения

и

и убедиться в выполнимости условия (8.14).

г) Включить выпрямитель в сеть и установить выходное напряжение – 4 В.

д) Нижнюю площадку-контакт расположить горизонтально и закрепить на заданном расстоянии h от тела m, удерживаемого электромагнитом. При этом тумблер «ПУСК» электромагнита должен находиться в нижнем положении и груз удерживаться магнитом.

е) Приготовить электросекундомер к измерению. Для этого необходимо: тумблер «ВКЛ.» поставить в верхнее положение и нажатием кнопки «СБРОС» установить нулевые показания на декатронах.

ж) Тумблер «ПУСК» на панели электромагнита поставить в верхнее положение. При этом одновременно замыкается цепь электросекундомера. Когда груз достигает площадки-контакта, цепь электросекундомера размыкается. По положению светящихся точек на декатронах отсчитываем время t падения груза в сотых долях секунды.

ЗАДАНИЯ

1. Изучить теорию, изложенную в работе.

2. Изучить экспериментальную установку.

3. Проверить выполнимость условия (8.9).

4. Найти моменты инерции тел по формуле (8.13) и (8.14).

5. Проверить выполнимость теоремы Штейнера, т.е. условия (8.15) и (8.16).

6. Оценить погрешность всех косвенных измерений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется угловой скоростью и угловым ускорением? Как располагаются векторы и ?

2. Что называется моментом силы и моментом импульса относительно неподвижной точки? Как определяются направления векторов и ?

3. Что называется моментом силы и моментом импульса относительно оси?

4. Что называется моментом инерции тела? Отчего он зависит? Как вычисляется момент инерции тела произвольной формы? Приведите примеры вычисления момента инерции тел простой формы.

5. Сформулируйте теорему Штейнера. Как можно на данной установке проверить теорему Штейнера?

6. Напишите и объясните уравнение второго закона Ньютона для вращательного движения.

7. Какие законы проверяются в данной работе?

8. Какие измерения вносят наибольшие погрешности?