Лаб.раб. по механике / ЛАБОРАТОРНАЯ РАБОТА №15

ЛАБОРАТОРНАЯ РАБОТА № 15

КОЛЕБАНИЕ СТРУНЫ

ЦЕЛЬ РАБОТЫ: экспериментально изучить стоячие волны на примере колебаний струны.

ОБОРУДОВАНИЕ: экспериментальная установка и необходимые принадлежности.

КРАТКАЯ ТЕОРИЯ

Общую теорию волновых процессов изучить по инструкции лабора-торной работе №14.

Пусть в безграничной упругой среде навстречу друг другу распространяется две плоские звуковые волны

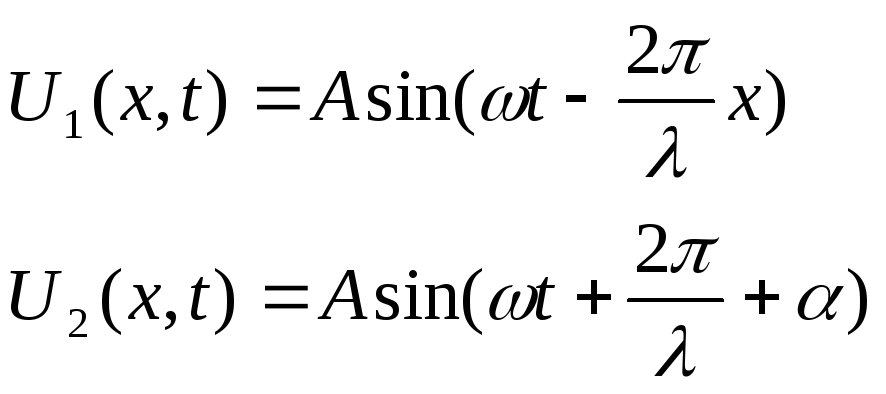, (15.1)

в которых колебания происходят в одном направлении (например, в вертикальном). В уравнении (15.1) - сдвиг фаз колебаний в точке среды с координатой . Результирующее колебание среды определяется уравнением

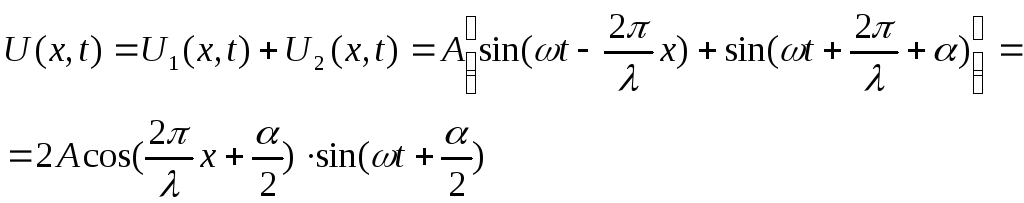(15.2)

Если сравнить это уравнение с уравнением гармонических колебаний точки, то оказывается, что множитель

(15.3)

-это амплитуда результирующего колебания. На рисунке 15.1 показана зависимость амплитуды от координаты .

Точки среды, в которых амплитуда волны максимальна, называются пучностями стоячей волны. Их координаты находятся из условия

(15.4)

Здесь

Точки среды, в которых амплитуда волны равна нулю, называются узлами стоячей волны. Их координаты находятся из условия

(15.5)

Здесь

Из приведенных формул следует, соседние узел и пучность отстают друг от друга на расстояние .

Множитель определяет зависимость амплитуды от времени. Этот множитель одинаков для всех точек среды. Если , то в момент времени все точки среды находятся в положении равновесия. Если , то в момент времени точки достигают своих наибольших отклонений. Причем там, где >0, точки находятся в верхнем положении, а где <0 – в нижнем (если ). После этого они начинают двигаться в противоположных направлениях, т.е. точки среды, находящиеся по разную сторону от узла колеблются в противофазах. Точки узла всегда остаются неподвижными. На рис.15.1 стрелками показаны направления движения точек среды после достижения крайних положений. Такие колебания называются стоячей волной.

Рассмотрим участок среды, у которого границы А и В закреплены (рис.15.2)

В этом случае в точках А и В амплитуда стоячей волны смещений т.е. на закрепленных границах образуются узлы.

Выражение (15.5) с учетом граничных условий и , где - номер последнего узла, можно записать:

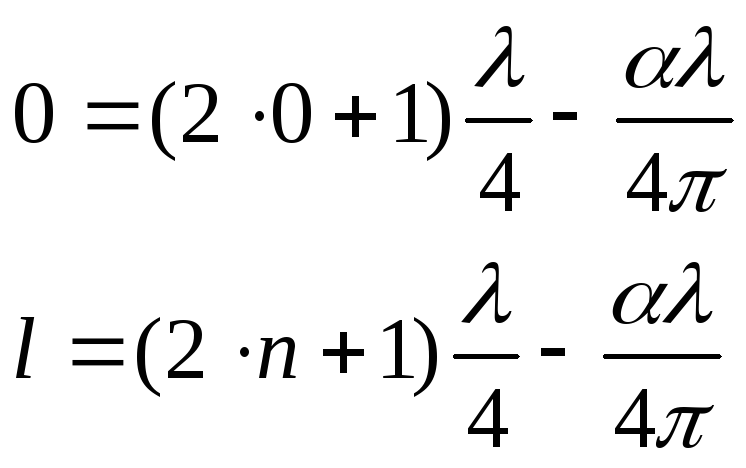
Решая эту систему, получим

(15.6)

Так как , то .Здесь длина стоячей волны.

Таким образом, на длине участка среды с закрепленными границами А и В укладывается целое число половин длин бегущей волны или целое число длин стоячей волны.

Найдем координаты узлов и пучностей стоячей волны смещений в данном случае. Воспользовавшись выражениями (15.4) , (15.5) и , получим

, (15.7)

где - порядковый номер узла.

, (15.8)

где - порядковый номер пучности.

Эти соотношения с учетом (15.6) можно записать

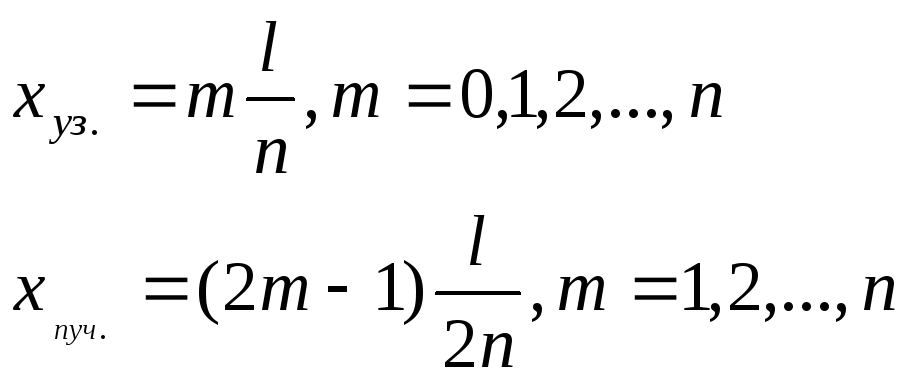(15.9)

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА, ТЕОРИЯ МЕТОДА И МЕТОДИКА ИЗМЕРЕНИЙ

Экспериментальная установка для получения стоячей волны состоит из стальной струны АВ, натянутой горизонтально между полюсами электромагнита М. Один конец струны А закреплен неподвижно, а на другой конец В, перекинутый через блок, прикрепляется груз Р, который сообщает струне постоянное натяжение. Изменяя величину груза Р, можно изменить величину натяжения струны.

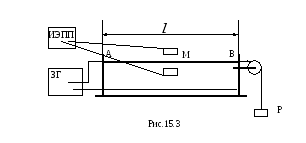
Магнит М можно перемещать вдоль струны. От звукового генератора по струне можно пропускать переменный ток звуковой частоты. Если по струне АВ = пропускать переменный ток , то на участок струны , заключенный между полюсами электромагнита, будет действовать переменная сила Ампера

,

где - индукция магнитного поля в зазоре электромагнита М,

- угол между направлением тока в струне и вектором магнитной индукции. В нашем случае , поэтому

.

Под действием переменной силы участок струны будет совершать вынужденные колебания (а вместе с ним и вся струна АВ). Если частота этих колебаний совпадает с одной из собственных частот колебаний струны, то возникает явление механического резонанса, а на струне образуется стоячая волна. В этом случае частота сигнала, посылаемого звуковым генератором, совпадает с собственной частотой колебания струны. Как показывает теория, собственная частота колебаний струны определяется по формуле

, (15.10)

где - максимальное число пучностей, возникающих на струне,

- длина струны,

- толщина струны,

- плотность материала струны,

- вес груза, создающего натяжение струны,

- собственная частота струны.

В данном случае можно записать, что или , а координаты узлов и пучностей определяются формулами

,

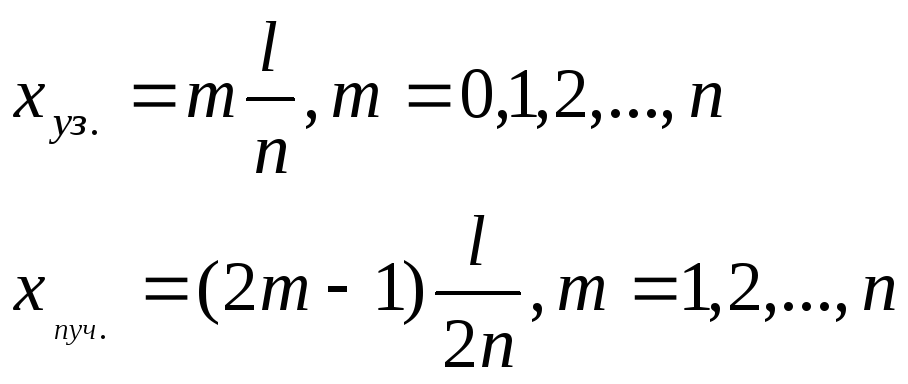где - максимальное число пучностей.

ЗАДАНИЕ 1

ТЕОРЕТИЧЕСКИЙ РАСЧЕТ ПАРАМЕТРОВ СТОЯЧЕЙ ВОЛНЫ

1. Изучите экспериментальную установку и теорию метода.

2. Используя формулу 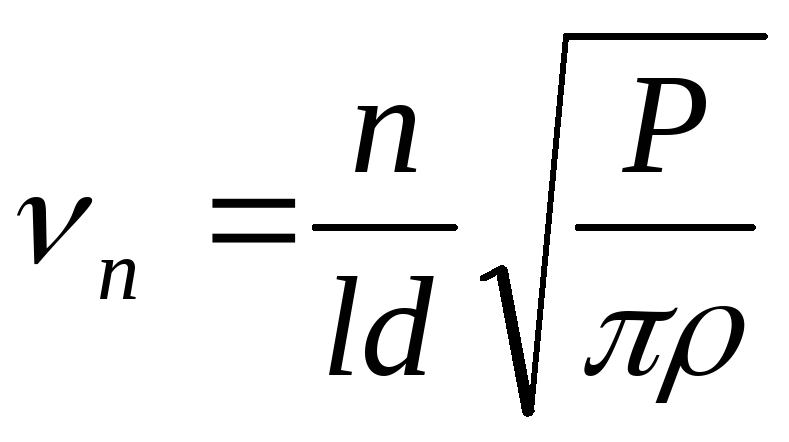и значение величины нагрузки, заданную преподавателем (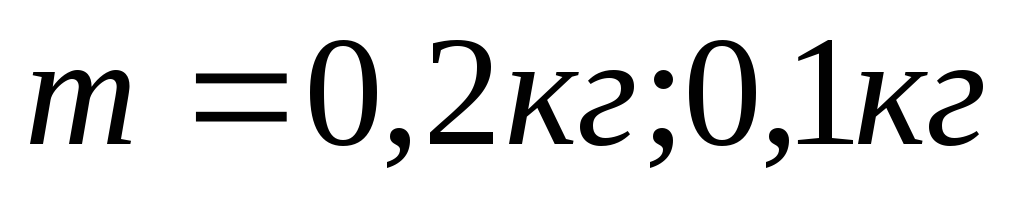), рассчитать частоты собственных колебаний струны для .

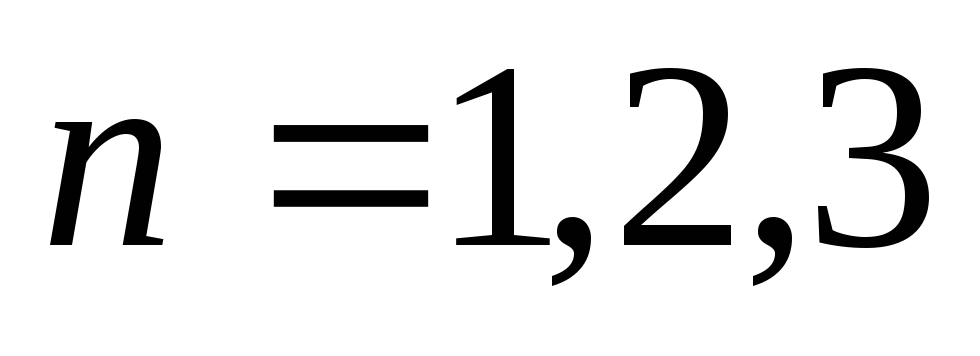3. Оцените погрешность измерений частот в пункте 2 и полученный результат запишите в виде 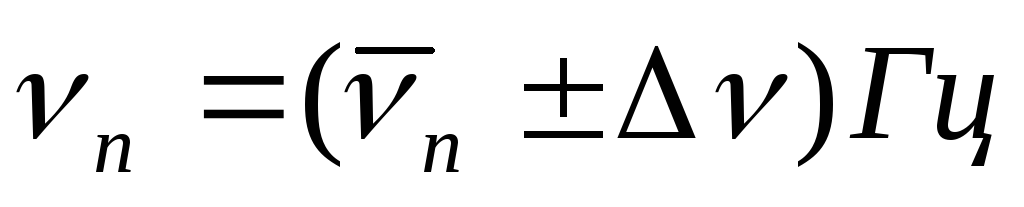, где .

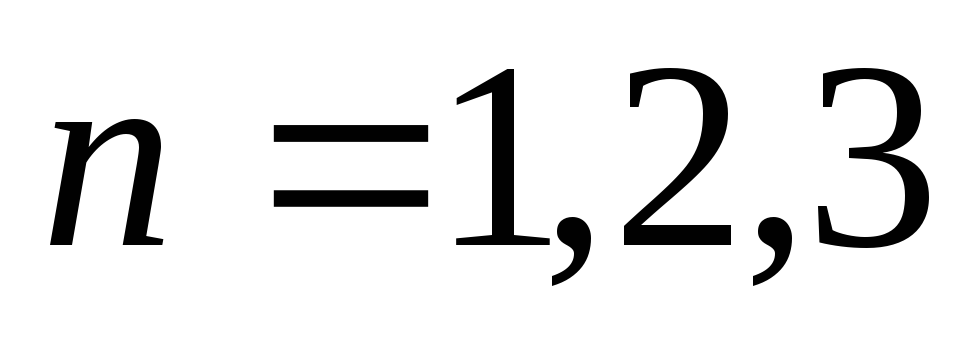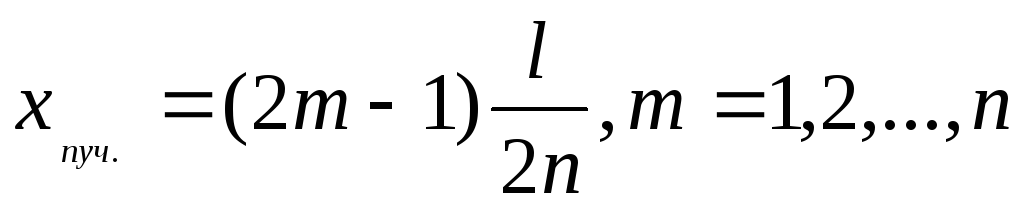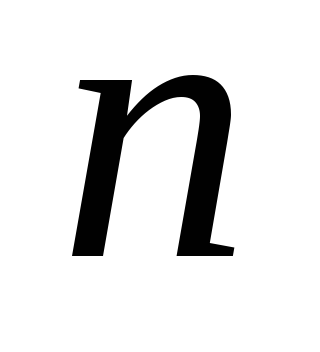4. Рассчитайте координаты пучностей по формуле , где - максимальное число пучностей на струне, 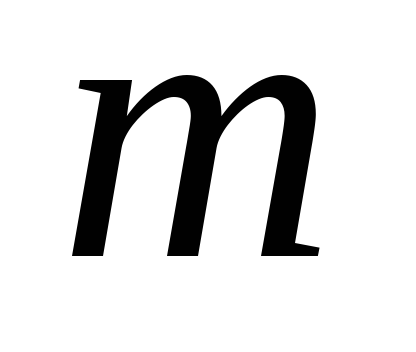- номер очередной пучности на струне, - длина струны.

5. Рассчитайте по формуле длину бегущих волн 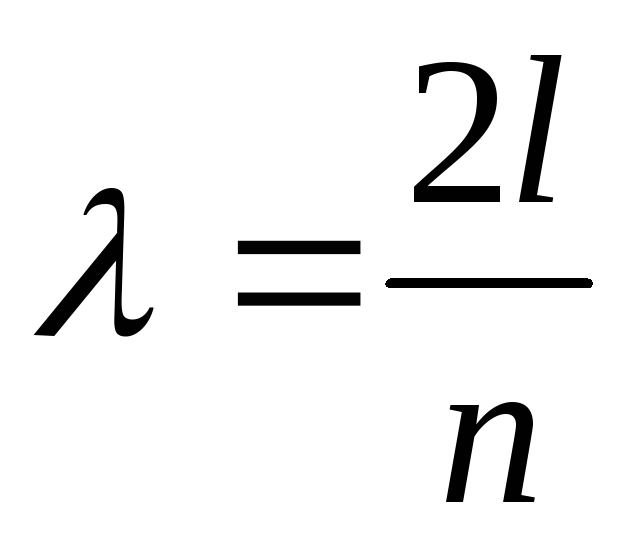, а также найдите длину стоячей волны 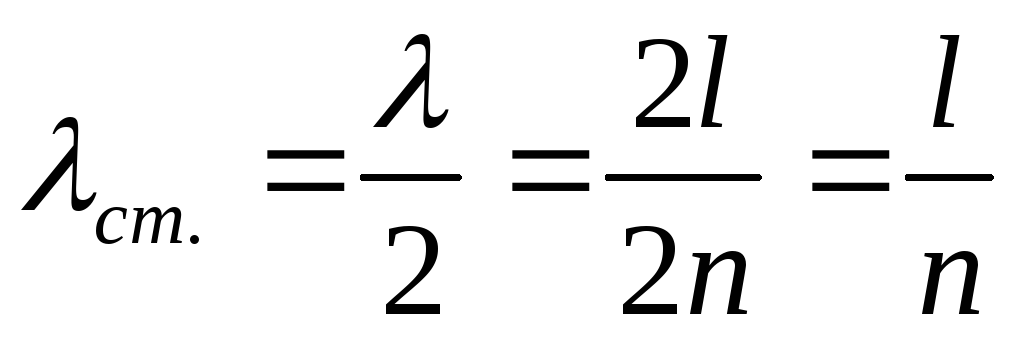, где - максимальное число пучностей на струне в заданном эксперименте.

6. Рассчитайте по формуле 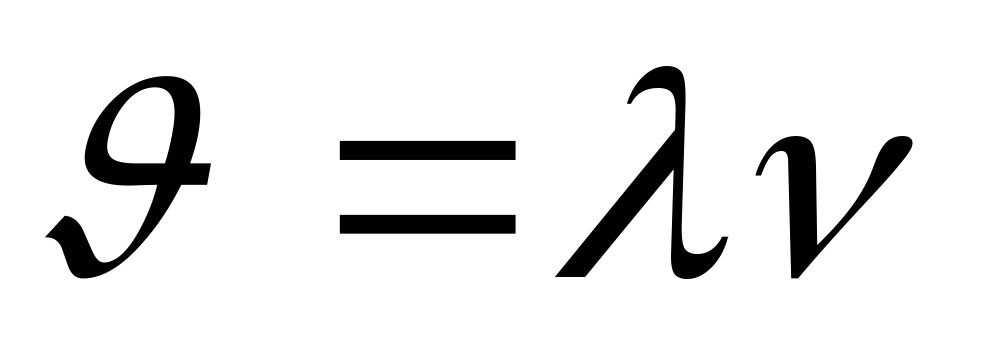скорость бегущих волн.

ЗАДАНИЕ 2

ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ СТОЯЧЕЙ ВОЛНЫ

1. Включите звуковой генератор в сеть.

2. Установите нагрузку 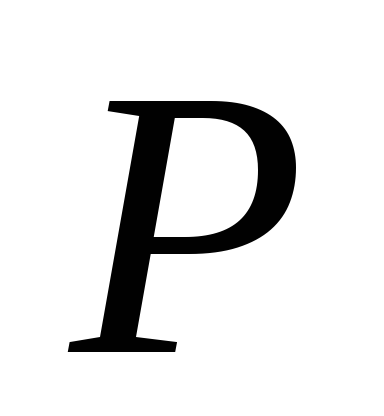, использованную в задании 1 в пункте 2.

3. Установите магнит М в точке с координатой , рассчитанной в пункте 4 задания 1 для .

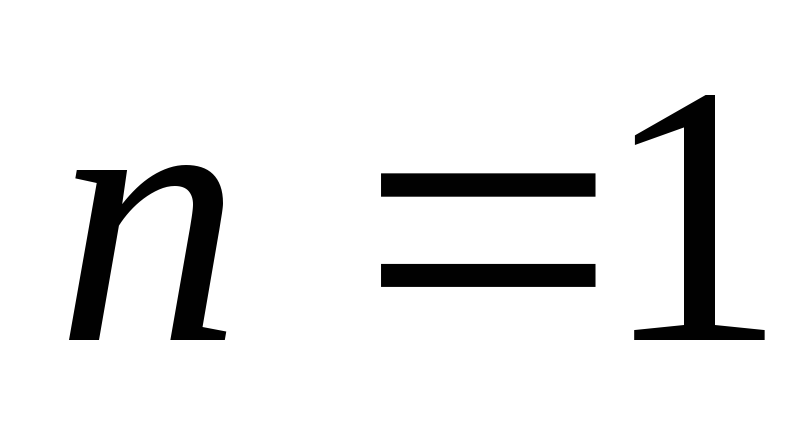4. Вращением лимба звукового генератора установите частоту электрического сигнала, равную частоте, рассчитанной в пункте 2 задания 1 для .

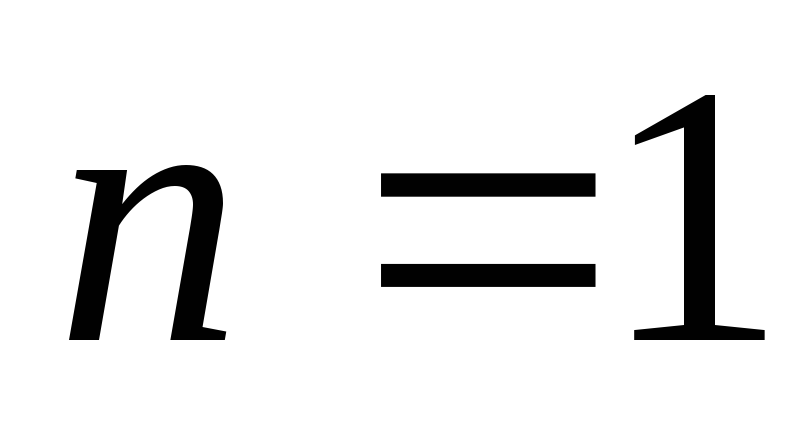5. Получите вынужденные колебания с максимальной амплитудой вращением лимба звукового генератора около частоты 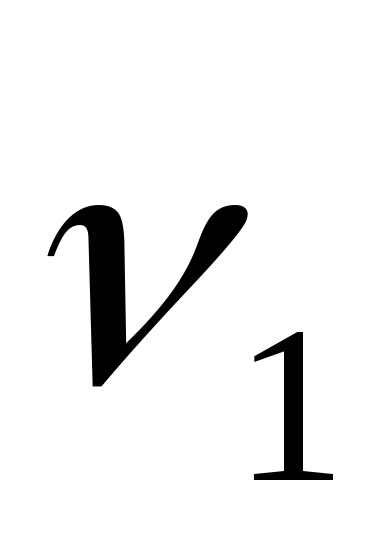и запишите показание лимба звукового генератора.

6. Оцените погрешность экспериментально измеренной частоты и сравните ее значение с .

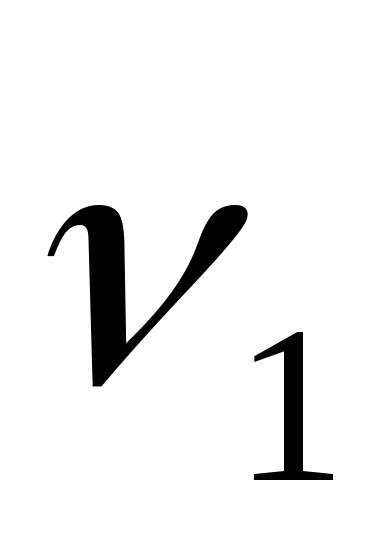7. Зарисуйте наблюдаемую стоячую волну.

8. Не меняя величину нагрузки , повторите пункты 3-7 для 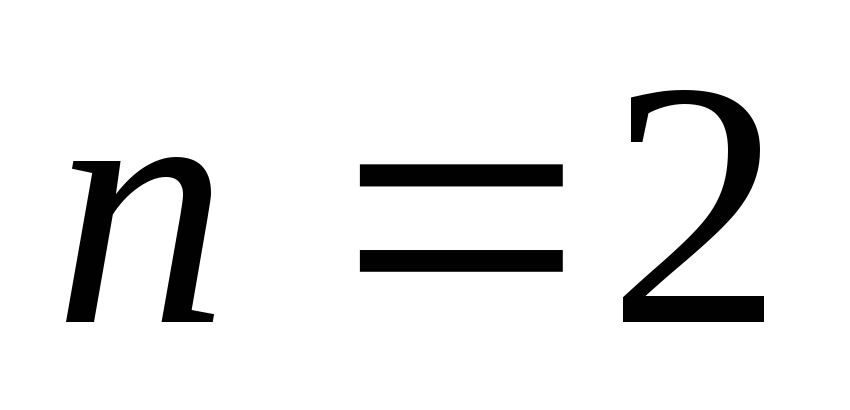и (по усмотрению преподавателя).

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Как образуется стоячая волна? Почему она называется стоячей?

2. Получите уравнение стоячей волны.

3. Что такое узлы и пучности стоячей волны?

4. Каковы особенности стоячей волны в ограниченном пространстве (на примере струны с закрепленными концами?

5. Что такое длина стоячей волны? Как она связана с длиной бегущей волны?

6. Как изменяется фаза стоячей волны при отражении от закрепленного конца?

7. Изложите физический принцип работы установки.