Лаб.раб. по механике / ЛАБОРАТОРНАЯ РАБОТА №12

ЛАБОРАТОРНАЯ РАБОТА № 12

ИЗУЧЕНИЕ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО МАЯТНИКА. ОПЫТНОЕ ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

ЦЕЛЬ РАБОТЫ:

1. Применить метод размерностей к выводу формулы периода колебаний математического маятника.

2. измерить с помощью маятника ускорение свободного падения.

ОБОРУДОВАНИЕ: экспериментальная установка.

КРАТКАЯ ТЕОРИЯ

Как известно , если на материальную точку массой действует возвращающая сила, пропорциональная смещению материальной точки из положения равновесия, то есть, если

, (12.1)

то оно совершает гармоническое колебание по закону

или (12.2)

с частотой или периодом .

М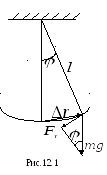атематический маятник – это тело малых размеров, колеблющееся на нити длиной . Пусть в некоторый момент времени математический маятник находится в положении, указанном на рис.12.1. Смещение маятника от положения равновесия определяется вектором , а действующая на маятник возвращающая сила равна . Если колебания малые (), то и, кроме того, векторы и примерно антипараллельны. Из рисунка видно, что , отсюда и возвращающая сила равна , или в векторном виде , здесь .

Таким образом, связана со смещением так же, как сила в формуле (12.1). Следовательно, математический маятник совершает гармонические колебания с периодом

(12.3)

Еще раз отметим, что эта формула тем лучше определяет период колебания, чем лучше удовлетворяется условие .

Из формулы (12.3) следует:

1. Период Т тем больше, чем больше длина .

2. Период Т зависит от g, следовательно, в разных местах на Земле период будет различный.

3. Период малых колебаний не зависит от амплитуды колебаний.

4. Период колебаний не зависит от массы колеблющегося тела (это свойство маятника следует из пропорциональности инертной и гравитационной масс).

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА И МЕТОДИКА ИЗМЕРЕНИЙ

Выражение для периода колебаний – важнейшая характеристика маятника – может быть получено не только путем решения дифференциального уравнения, но и с помощью более простого, но чрезвычайно важного в физике метода размерностей.

Можно предположить, что период колебаний зависит от длины маятника , массы и ускорения свободного падения так, что эту зависимость можно записать в виде степенного соотношения-

(12.4)

где - безразмерный коэффициент, а - подлежащие определению показатели степени. Приравняем размерности левой и правой части уравнения (12.4)

(12.5)

где - обобщенные обозначения единиц времени, массы и длины. Сравнивая показатели при слева и справа, будем иметь . Отсюда . Учитывая этот результат, (12.4) можно записать в виде

(12.6)

Правило размерностей не позволяет определить безразмерную постоянную .

В задачу данной работы входит экспериментальное определение показателей и постоянной . Прологарифмируем выражение (12.4)

(12.7)

Из (12.7) следует, что

1. Для того, чтобы найти , необходимо определить, по крайней мере, два периода колебаний Т₁ и Т₂ для двух различных масс m₁ и m₂ маятника при условии . Тогда из (12.7) легко получить

(12.8)

2. Для того, чтобы найти , необходимо определить два периода колебаний Т₁ и Т₂ для двух различных длин маятника и при условии . Тогда

(12.9)

3. Число в данной работе найти нельзя, так как из формулы следует, что необходимо произвести измерения двух периодов колебаний при двух различных значениях . Поэтому примем, что входит в формулу (12.5) в степени 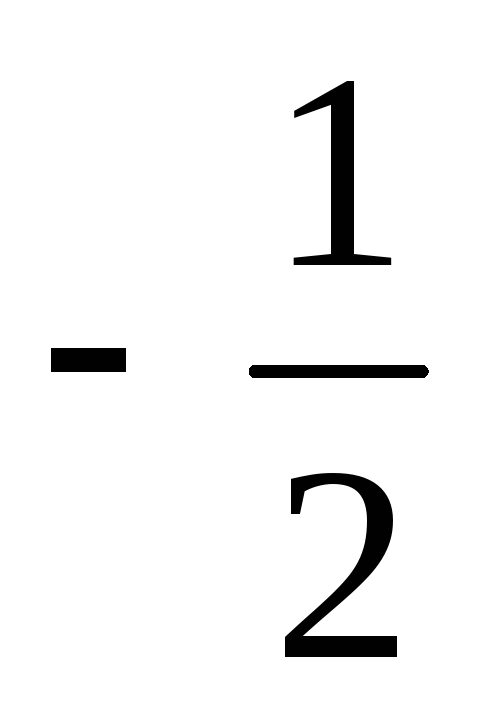как это следует из правила размерностей.

4. Безразмерный коэффициент А нельзя найти методом размерностей. К счастью, во многих случаях он близок к единице. Но в некоторых случаях он существенно отличается от единицы. Формула для периода математического маятника – один из этих примеров.

5. Определение ускорения свободного падения с помощью математического маятника.

Математический маятник можно применить для определения ускорения свободного падения. Пусть Т₁ и Т₂ - периоды колебаний маятника при двух длинах нитей и (рис.12.2). Тогда на основании можно записать

(12.10)

Возведя (12.10) в квадрат и вычитая одно из другого, получим:

. Отсюда .

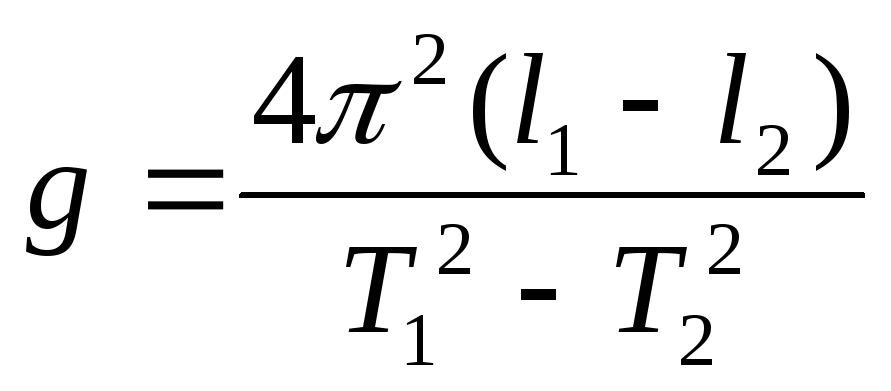ПРИМЕЧАНИЕ. Формула не используется непосредственно для определения ускорения свободного падения, так как не всегда известно положение центра масс маятника.

Экспериментальная установка представляет собой математический маятник с изменяемой длиной, которую можно определить по миллиметровой шкале. Масса маятника изменяется навинчиванием дополнительных грузов. Период колебаний определяется с помощью секундомера по числу колебаний.

ЗАДАНИЯ

1. Изучите теорию данного вопроса.

2. Изучите экспериментальную установку и порядок работы с ней.

3. Используя метод размерностей, определите экспериментально показатели и .

4. Определите период колебания маятника при различных начальных углах отклонения нити. Возьмите углы 10^о, 20^о, 30^о, 40^о, 50^о и постройте график зависимости периода от угла отклонения. Какие колебания можно считать малыми?

5. Определите с помощью математического маятника ускорение свободного падения.

6. Оцените погрешности косвенных измерений.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Дайте определение математического маятника.

2. Изложите способ определения зависимости Т от на основе теории размерностей.

3. Изложите суть экспериментального способа определения зависимости Т от .

4. Почему в данной работе не определяется число ? Опишите условия, в которых можно было бы измерить .

5. Запишите формулу для определения периода колебаний математического маятника и проанализируйте смысл в нее входящих величин.

6. Выведите рабочую формулу для определения ускорения свободного падения.

7. Изменится ли период маятника от того, что мы его поместим в воду? Маятнику придана обтекаемая форма и можно считать, что трение о воду равно нулю.

8. Получите формулы погрешностей косвенных измерений.