
Прикл математика май 2014 / Методичка по прикладной математике
.pdf
Кафедра высшей математики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
и контрольные задания по курсу «Прикладная математика»
для студентов – заочников направлений
110800.62 - |
Агроинженерия |
190600.62 - Эксплуатация транспортно-технологических машин и комплексов
САНКТ-ПЕТЕРБУРГ
2014

М е т о д и ч е с к и е у к а з а н и я к онтрольные задания по курсу «Прикладная
математика»/ сост. И.Н. Шоренко.- Санкт-Петербург, СПбГАУ, 2014, с.
Приведены краткие сведения и формулы по темам «Численные методы» и «Статистические методы обработки опытных данных». На примере типовых заданий рассмотрены способы реализации численных методов и методов обработки опытных данных средствами Microsoft Excel. Приведены контрольные задания для самостоятельного решения.
Предназначены для студентов-заочников 3-го курса направлений
«Агроинженерия» и «Эксплуатация транспортно-технологических машин и комплексов»,
изучающих дисциплину «Прикладная математика».
Составитель: канд. техн. наук И.Н. Шоренко
Рецензент
Шоренко И. Н., 2012
ФГБОУ ВПО СПбГАУ,
2012
.
2

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНРЙ РАБОТЫ
Основной формой обучения студентов-заочников является самостоятельная работа над учебным материалом. Учебный материал следует изучать в той последовательности,
которая приведена в методических указаниях. После изучения теоретических вопросов надо перейти к разбору решенных в методических указаниях заданий. Затем можно
переходить к решению соответствующей задачи из контрольного задания.
Выполненное контрольное задание должно быть напечатано на листах формата А4. На обложке должна быть указана фамилия студента, направление обучения, номер группы, шифр (номер зачетной книжки), номер варианта, фамилия преподавателя,
который проверяет задание.
При выполнении контрольных заданий следует учесть следующие рекомендации:
необходимо указывать номер задания и полностью записывать его условие;
решения заданий надо располагать в порядке номеров, указанных в заданиях;
решение всех задач сопровождать при необходимости пояснениями, ссылаясь на положения теории.
На зачете студент должен представить выполненное задание и в электронном виде.
После получения прорецензированной работы студент обязан выполнить все указания рецензента и исправить ошибки. Исправленная контрольная работа должна быть направлена на повторное рецензирование.
В тех случаях, когда студент при изучении теории или решении задач встретит
затруднения, которые самостоятельно разрешить не сможет, он может обратиться за консультацией на кафедру высшей математики СПбГАУ.
Студент выполняет тот вариант контрольного задания, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в табл.1, если же предпоследняя цифра учебного шифра есть число четное или нуль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в табл.2.
3
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
Вариант |
|
Номера задач контрольного задания |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
11 |
31 |
51 |
71 |
91 |
|
|
|
|
|
|
|
|
2 |
12 |
32 |
52 |
72 |
92 |
|
|
|
|
|
|
|
|
3 |
13 |
33 |
53 |
73 |
93 |
|
|
|
|
|
|
|
|
4 |
14 |
34 |
54 |
74 |
94 |
|
|
|
|
|
|
|
|
5 |
15 |
35 |
55 |
75 |
95 |
|
|
|
|
|
|
|
|
6 |
16 |
36 |
56 |
76 |
96 |
|
|
|
|
|
|
|
|
7 |
17 |
37 |
57 |
77 |
97 |
|
|
|
|
|
|
|
|
8 |
18 |
38 |
58 |
78 |
98 |
|
|
|
|
|
|
|
|
9 |
19 |
39 |
59 |
79 |
99 |
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
||
Вариант |
|
Номера задач контрольного задания |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
21 |
41 |
61 |
81 |
|
|
|
|
|
|
|
|
2 |
2 |
22 |
42 |
62 |
82 |
|
|
|
|
|
|
|
|
3 |
3 |
23 |
43 |
63 |
83 |
|
|
|
|
|
|
|
|
4 |
4 |
24 |
44 |
64 |
84 |
|
|
|
|
|
|
|
|
5 |
5 |
25 |
45 |
65 |
85 |
|
|
|
|
|
|
|
|
6 |
6 |
26 |
46 |
66 |
86 |
|
|
|
|
|
|
|
|
7 |
7 |
27 |
47 |
67 |
87 |
|
|
|
|
|
|
|
|
8 |
8 |
28 |
48 |
68 |
88 |
|
|
|
|
|
|
|
|
9 |
9 |
29 |
49 |
69 |
89 |
|
|
|
|
|
|
|
|
0 |
10 |
30 |
50 |
70 |
90 |
|
|
|
|
|
|
|
|
4

Задание 1. Численные методы решения нелинейных уравнений
1. Аналитически и графически способом определить количество корней уравнения
2x x2 3 и интервалы, на которых корни расположены.
2.Вычислить какой-либо корень уравнения с точностью до 0,001 методами:
половинного деления, хорд, касательных.
|
1. Отделение корней уравнения |
|
|
|
|
|
|
|||||
|
|
Сформулируем условия, при выполнении которых можно утверждать, что на |
||||||||||
|
отрезке [a,b] существует корень уравнения f (x) |
0 . |
|
|
|
|
||||||
|
|
Теорема. Пусть функция |
f (x) , непрерывная и монотонная на отрезке [a,b] . |
|||||||||
|
Если значения функции |
f (a) и |
f (b) имеют разные знаки ( f (a) f (b) |
0 ), то внутри |
||||||||
|
интервала (a,b) функция имеет корень и притом единственный; |
|
|
|||||||||
|
Если |
значения функции |
f (a) и f (b) |
имеют одинаковые знаки ( f (a) |
f (b) |
0 ), то |
||||||
|
внутри интервала (a,b) |
функция корней не имеет. |
|
|
|
|
||||||
1. |
Уравнение 2x |
x2 |
3 заменим равносильным 2x |
x2 |
3 |
0 |
|
|
||||
2. |
Построим таблицу значений аргумента |
x и значений |
функций f (x) |
2x |
x2 3 и |
|||||||
|
f (x) |
2x ln 2 |
2x |
на |
некотором интервале |
[a,b] |
и |
определим «соседние» |
||||
промежуточные значения xi и xi 1 , для которых функция f (x) примет значения разных знаков. Выберем начальное a и конечное b значения аргумента x с учетом
области определения функции |
f (x) |
и шаг табулирования h . Например, |
|||||
a |
4, |
b 6 |
, h |
b |
a |
0,5 |
|
20 |
|||||||
|
|
|
|
|
|||
В ячейку А8 копируем начальное значение a , в ячейках B9 и C9 разместим формулы для вычисления значений функций f (x) и f (x) . В ячейке А10 запишем формулу для вычисления следующего значения аргумента, в ячейки B10 и C10 копируем формулы из ячеек B9 и C9. В ячейке D10 поместим проверку условия существования корня с помощью функции ЕСЛИ:
если f (xi ) 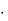 f (xi 1 ) 0,
f (xi 1 ) 0,
то печатаем «корень находится на интервале» и интервал (xi 1 , xi ) ,
в противном случае печатаем пробел.
Процесс копирования формул А10:D10 нужно продолжить до конца интервала
(значения b ), на котором хотим проверить наличие корней уравнения. Если на
5

выбранном интервале [a,b] корни не найдены, то меняем значения a и b . Значения a
и b нужно подобрать так, чтобы все корни уравнения находились на интервале [a,b] .
3.Для получения более наглядного представления о функции f (x) построим ее график на интервале [a,b]. Выделим ячейки А8:В29 и выполним операции Вставка → Точечная диаграмма → Точечная с гладкими кривыми. Значения x , при которых
график функции f (x) пресекает ось ОХ, является корнем уравнения f (x) 0 .
Для рассматриваемого уравнения 2x x2 3 0 видно, что уравнение имеет единственный корень, который находится на отрезке [4,5; 5].
6
2.Вычисление корней уравнения
Метод половинного деления
|
|
Пусть уравнение |
f (x) |
|
0 имеет единственный корень на конечном интервале |
|||||||||||||||||||||||
(a,b) , |
функция |
y |
f (x) |
непрерывна на интервале [a,b] и принимает на его концах |
||||||||||||||||||||||||
значения разных знаков ( f (a) |
|
f (b) |
0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Обозначим исходный промежуток |
[a,b] [a0 ,b0 ]. Пусть |
c0 |
|
a0 |
b0 |
– |
середина |
||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этого отрезка. Вычислим |
|
f (c ) |
. Если |
f (c ) |
0, |
то корень найден и x* c . |
В |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
противном случае |
(если f (c0 ) |
0) из двух половин отрезка [a0 ,b0 ] |
выбираем ту, |
на |
||||||||||||||||||||||||
концах |
которой |
|
f (x) |
имеет |
противоположные |
знаки. |
Выбранную |
половину |
||||||||||||||||||||
обозначим [a1,b1] . |
Повторим |
процедуру |
деления |
отрезка: |
c1 |
a1 |
|
b1 |
середина |
|||||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отрезка [a1,b1] . |
Пусть |
[a2 ,b2 ] - |
та половина отрезка [a1,b1] , |
где |
f (a2 ) |
f (b2 ) |
0; |
|||||||||||||||||||||
c |
|
a2 |
b2 |
|
- середина |
[a ,b ]. Продолжая процедуру деления и выбирая каждый раз |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тот отрезок, |
на котором функция меняет знак, на n -ом шаге получим отрезок [an ,bn ]: |
|||||||||||||||||||||||||||
f (an ) |
f (bn ) 0. |
Корень считается найденным, |
если длина этого отрезка |
меньше |
||||||||||||||||||||||||
заданной погрешности |
, т.е. |
|
bn |
an |
|
. За приближенное значение корня берется |
||||||||||||||||||||||
середина последнего отрезка c |
|
|
an |
bn |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
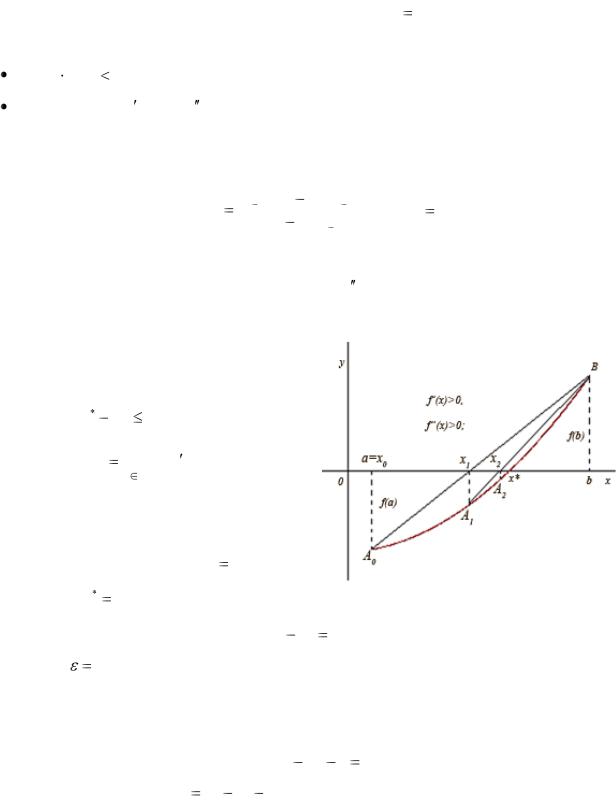
|
Методом половинного деления найдем корень уравнения 2x |
x2 |
3 , |
находящийся |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
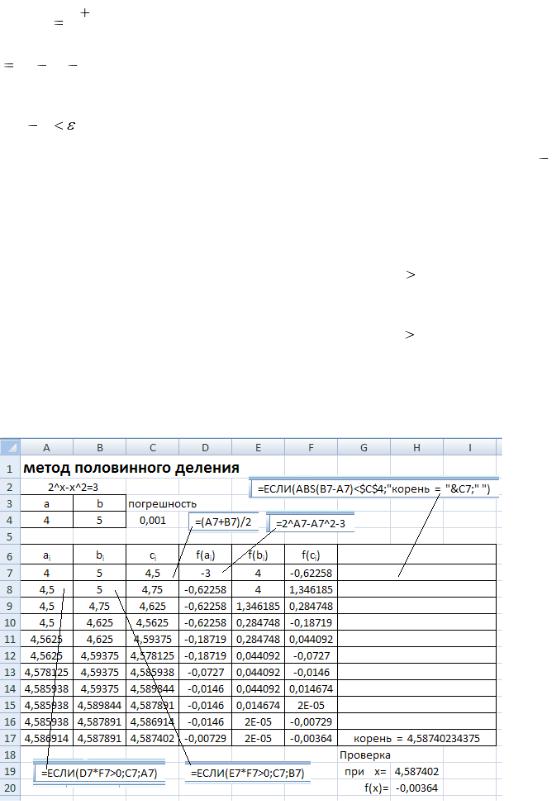
на интервале [4,5; 5] с точностью до 0,001.
1.В ячейках А4 и В4 разместим исходные данные – границы отрезка [a,b], на котором находится корень уравнения и допустимую погрешность 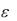 (D4).
(D4).
2.В ячейки А7 и В7 помещают ссылки на исходные данные, в ячейке С7 вычисляется
значение |
c |
a |
|
b |
- середины |
отрезка, в ячейках D7:F7 - значения функции |
||
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
f (x) 2x |
|
x2 |
|
3 в указанных точках. В ячейке G7 указывается условие, при котором |
||||
корень уравнения считается найденным, и найденное значение корня. |
||||||||
|
a |
|
|
|
«корень =» и найденное значение корня с , в |
|||
Если |
b |
|
|
, то печатаем |
||||
|
|
|
|
|
|
|
|
|
противном случае « корень не найден». Для вычисления модуля разности b a
используется функция ABS.
3.В ячейках А8 и В8 из отрезков [a,c] и [c,b]выбирается тот, на концах которого функция f (x) имеет значения разных знаков:
если значения f (a) и f (c) одного знака ( f (a) 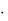 f (c) 0 ), то значение a
f (c) 0 ), то значение a
заменяем на c , в противном случае a оставляем без изменения;
если значения f (b) и f (c) одного знака ( f (b)  f (c) 0 ), то значение b
f (c) 0 ), то значение b
заменяем на c , в противном случае b оставляем без изменения.
В ячейки C8:G8 копируем содержимое ячеек C7:G7.
4.Формулы А8:G8 распространяются вниз до получения ответа.
8
Метод хорд
Пусть x - единственный корень уравнения f (x) 0 , который находится на отрезке [a,b]. Функция f (x) удовлетворяет следующим условиям:
- единственный корень уравнения f (x) 0 , который находится на отрезке [a,b]. Функция f (x) удовлетворяет следующим условиям:
f (a) f (b) |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
производные f (x) и f (x) |
функции, |
f (x) |
непрерывны и сохраняют постоянные |
||||||||||||||||||
знаки на отрезке [a,b]. |
|
|
|
|
|
|
|
|
|
||||||||||||
Общая формула метода хорд имеет вид |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
xn 1 f (c) |
cf (xn 1 ) |
, |
n 1, 2, ... |
(1.1) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
f (c) |
f (xn 1 ) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В качестве |
c нужно взять тот конец отрезка [a;b], для которого знак функции |
||||||||||||||||||||
f (x) совпадает со знаком ее второй производной |
f |
(x) , а за |
начальное приближение x0 |
||||||||||||||||||
следует принять другой конец этого отрезка. |
|
|
|
|
|
|
|||||||||||||||
Для |
оценки погрешности |
используем |
|
|
|
|
|
||||||||||||||
неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
xn |
|
|
|
f (xn ) |
|
, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где m |
|
|
min |
f (x) |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x [a,b] |
|
|
|
|
|
n - м |
|
|
|
|
|
|
|
|||||
Если |
|
это |
условие |
на |
шаге |
|
|
|
|
|
|||||||||||
выполнено, то в качестве приближенного |
|
|
|
|
|
||||||||||||||||
значения корня уравнения |
f (x) |
0 берут xn |
|
|
|
|
|
||||||||||||||
|
|
x |
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1 |
|
|
Вычислим |
корень |
уравнения |
2x |
x2 3, |
принадлежащий отрезку |
[4,5; 5], с |
|||||||||||||||
точностью |
0,001. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.Оформим процедуру вычисления на листе Excel: укажем название метода, уравнение,
интервал [a; b] на котором находится корень уравнения, погрешность. Преобразуем
уравнение: |
2x x2 3 0 |
2. Проверим, что функция f (x) 2ч |
x2 3 удовлетворяет необходимым условиям. |
9
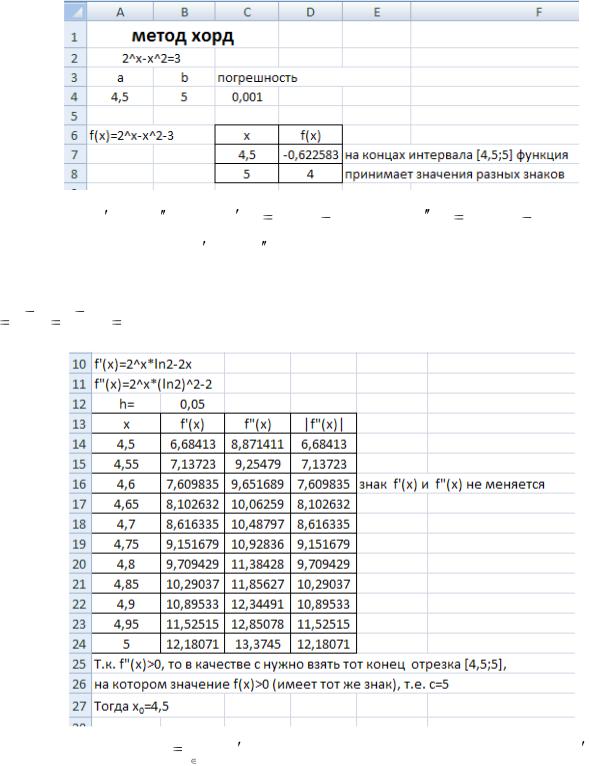
|
Найдем f (x) |
и f (x) : |
f (x) |
2x ln 2 2x , |
f (x) |
2x ln2 2 |
2 . |
||
|
Исследование знаков f (x) и f |
(x) можно провести аналитически либо построив |
|||||||
таблицу |
значений |
|
этих функций |
на отрезке |
[4,5; 5] с |
шагом, |
например, |
||
h |
b a |
5 4,5 |
0,05. |
|
|
|
|
|
|
10 |
10 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Найдем значение m min |
f (x) |
. |
Построим таблицу значений |
f (x) |
x [4,5;5] |
|
|
|
|
(функция ABS) и выберем из них наименьшее, используя функцию МИН. |
|
|||
3.Введем исходные данные для вычислений ( x0 , c , f (c) , m ) и построим таблицу, в
которой по формуле (1.1) будут вычисляться последовательные значения xn и
оцениваться их погрешности.
10
