Лекции / лекци 7хх первичная обработка

ЛЕКЦИЯ 7ХХ

ПЕРВИЧНОЕ ПРЕОБРАЗОВАНИЕ ИНФОРМАЦИИ И КОДИРОВАНИЕ СИГНАЛОВ.

ЦЕЛЬ ЛЕКЦИИ: Охарактеризовать методы первичного преобразования информации в ТКС. Привести описание методов аналого-цифрового преобразования, дискретного преобразования Фурье и дискретного косинусного преобразования.

Усвоив основные положения теории информации, перейдем к изучению примеров практического применения этих положений в технике телекоммуникационных систем (ТКС). Следует отметить, что при изучении теории информации в процессе доказательства теорем нами использовались понятия “алфавит” и “символ”, которые , как правило, означали алфавит и буквы определенного языка, причем сообщение представлялось в виде текста. В практике реальных ТКС используются и другие “алфавиты”. При этом разработчику ТКС приходится иметь дело с источниками информации различного вида и, зачастую, самому формировать “алфавит” конкретного источника, применяя к сигналу источника информации предварительную обработку с целью получить “символы” для кодирования их и передачи по каналу связи.

В качестве примера рассмотрим требования к каналу передачи цифрового телевизионного сигнала.

Поскольку видеоизображение преобразуется в цифровую форму, следует оценить возможности современных линий связи при передаче потока цифровых данных. На входе кодера видеоизображение подвергается предварительной обработке - аналого - цифровому преобразованию, при котором выполняются операции дискретизации по времени и квантования по уровню. В соответствии с теоремой отсчетов частота дискретизации f должна быть не менее, чем в два раза выше верхней частоты в спектре передаваемого сигнала F , т. е. F = 2 f. При российском стандарте 6 МГц для верхней частоты яркостного сигнала изображения F = 12 МГц. Требование унификации параметров цифрового потока для различных стандартов разложения изображения на строки повышает F до 13,5 МГц. При цифровом методе кодирования видеоизображения используются два цветоразностных сигнала, частота дискретизации которых составляет F/2. Такой стандарт цифровой передачи изображения обозначают 4:2:2. При квантовании по уровню используется восьмиразрядное кодирование. Итоговая скорость передачи цифрового потока для данного стандарта

V = 13,5+2х6,75х8 = 216 Мбит/сек.

Передача изображений с такой скоростью по каналу VHF или UHF диапазонов невозможна. Задача предварительной обработки и сжатия изображения в данном случае становится первостепенной.

Сразу же отметим, что в современной телефонии подобная задача не менее актуальна.

Специалисту в области ТКС необходимо знание цифровых технологий и методов обработки данных для передачи по каналу связи.

Фундаментальной основой развития телекоммуникационных систем является цифровая обработка информации. Сущность цифровой обработки состоит в том, что физический сигнал преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве. Исходный физический сигнал является непрерывной функцией времени.

Сигналы, определенные во все моменты времени, называются

аналоговыми.

Последовательность чисел, представляющая сигнал при цифровой обработке, называется дискретным рядом. Дискретный ряд состоит из отсчетов.

Отсчетом является значение сигнала в отдельные (дискретные) моменты времени. Как правило отсчеты берутся через равные промежутки времени.

Промежуток времени между отсчетами называется периодом дискретизации или интервалом, шагом дискретизации.

Величина, обратная периоду дискретизации, называется частотой дискретизации.

Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией, а результат такого преобразования - дискретным сигналом.

Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню.

Сигнал дискретный во времени, но не квантованный по уровню, называется дискретным.

Сигнал, дискретный во времени и квантованный по уровню, называется цифровым.

На рисунке представлены все три вида сигналов.

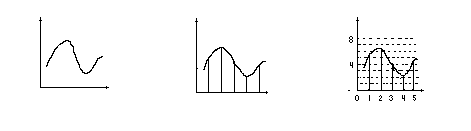
Аналоговый сигнал Дискретный сигнал Цифровой сигнал

Рис. 1 Преобразование аналогового сигнала в цифровой.

Из рисунка, поясняющего операции формирования цифрового сигнала видно, что процесс квантования порождает ошибки квантования, вследствие несовпадения действующего значения дискретной величины и уровня квантования. Возникающие в процессе квантования ошибки округления называются шумами квантования

Аналого - цифровое преобразование.

Дискретизация.

При выборе частоты дискретизации f_д должно выполняться условие теоремы Котельникова f_д >f _в , где f_в – верхняя граничная частота спектра преобразуемого в цифровую форму сигнала. В результате дискретизации получается дискретный сигнал (последовательность выборок), по которому с помощью операции интерполяции можно восстановить исходный сигнал. (дать рисунок на доске).

Спектр дискретного сигнала.

Для понимания процесса восстановления сигнала по его дискретным отсчетам рассмотрим спектр дискретного сигнала. Дискретный сигнал после преобразования представлен последовательностью чисел. Поэтому для анализа обычными (аналоговыми) средствами необходимо сопоставить этой последовательности некоторую функцию. Один из способов такого представления является представление отсчетов в виде дельта-функций с соответствующими множителями и задержками. Последовательность отсчетов x(k) будет описана следующим образом

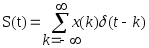
[1]

Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра на комплексную экспоненту. Все это позволяет сразу же записать спектр дискретного сигнала

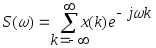
[2]

Из этой формулы видно главное свойство спектра любого дискретного сигнала: спектр является периодическим, его период в данном случае равен 2π (т.е. круговой частоте дискретизации, поскольку, составляя сигнал из дельта-функций, мы выбрали единичный интервал между ними, что дает ω_д =2 π):

S(ω+2π) = S(ω)

Обратим внимание на размерность спектральной функции дискретного сигнала: она совпадает с размерностью отсчетов. Это связано с тем, что дельта-функции времени, из которых был составлен сигнал, имеют размерность частоты.

Формула [2] позволяет вычислить спектральную функцию по известным отсчетам x(k). При конечном числе ненулевых отсчетов этот расчет несложен и может быть выполнен с помощью функции MATLAB freqz. (для владеющих пакетом MATLAB)

Рассмотрим несколько иную задачу.

Пусть значения x(k) являются отсчетами аналогового сигнала s(t), взятыми с периодом Т.

X(k) = s(kT)

Выясним, как в этом случае спектр дискретного сигнала [2] связан со спектром аналогового сигнала S(ω ). Мы рассматриваем дискретизированный сигнал в виде последовательности дельта-функций, “взвешенной” значениями отсчетов s(kT) аналогового сигнала s(t).

[3]

Так как функция δ(t – kT) равна нулю всюду, кроме момента t = kT, можно заменить в выражении [3] константы s(kT) на исходный непрерывный сигнал s(t):

[4]

Далее заметим, что сумма, входящая в выражение [4], является периодическим сигналом, а потому может быть представлена в виде ряда Фурье. Коэффициенты этого ряда равны

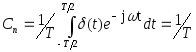
[5]

В формуле [5] было учтено, что в интервал интегрирования (- T/2, T/2) попадает только одна дельта-, функция соответствующая k=0. Таким образом, периодическая последовательность дельта-функций может быть представлена в виде комплексного ряда Фурье.

[6]

где ω =2πn/T. Подставив [6] в [4], получим

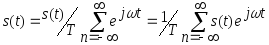
Умножение сигнала на экспоненту exp(jωt) соответствует сдвигу спектральной функции на ω, поэтому спектр дискретизированного сигнала можно записать следующим образом

[7]

Таким образом, спектр дискретизированного сигнала представляет собой бесконечный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t). Расстояние по частоте между соседними копиями спектра равно частоте дискретизации ω =2π /T, что наглядно иллюстрируется рисунком.

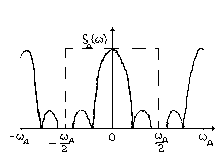
Рис. 1 Спектр дискретизированного сигнала.

Следует также отметить, что из-за наличия в формуле [7] множителя 1/T спектр дискретизированного сигнала имеет размерность, совпадающую с размерностью сигнала (поскольку дельта-функция имеет размерность частоты).

Характер спектра дискретизированного сигнала демонстрирует частотно-временную дуальность преобразования Фурье:

Периодический сигнал → частотный спектр

Периодический спектр → дискретный сигнал

Отметим следующее. Формула [2] позволяет рассчитать спектр последовательности отсчетов x(k), не связывая эти отсчеты с аналоговым сигналом. Формула [7] предполагает, что отсчеты x(k) получены путем дискретизации аналогового сигнала s(t), и показывает связь между спектрами дискретизированного и аналогового сигналов. Обе формулы дают одинаковый результат. Отсюда следует важный факт. Соединить отсчеты x(k) для получения аналогового сигнала можно произвольным образом. В каждом случае аналоговый сигнал будет иметь, конечно, свой спектр. Однако результат суммирования сдвинутых копий спектров по формуле [7] всегда будет одним и тем же, поскольку определяется только значениями дискретных отсчетов x(k) = s(kT) и формулой [2].

Рисунок, приведенный выше, демонстрирует и способ восстановления непрерывного сигнала по дискретным отсчетам. Для этого необходимо пропустить дискретный сигнал через идеальный фильтр нижних частот (ФНЧ) с частотой среза, равной половине частоты дискретизации. Амплитудно-частотная характеристика такого фильтра показана на рисунке пунктиром. Очевидно, что точное восстановление сигнала возможно, если сдвинутые копии спектра не перекрываются. Из рисунка видно, что для этого необходимо, чтобы частота дискретизации как минимум в два раза превышала верхнюю частоту спектра сигнала: ω_д 2 ω_в..

Квантование.

Число уровней квантования M_кв , определяемое числом двоичных разрядов АЦП n в соответствии с соотношением M_кв = 2^N – важнейший параметр преобразования.

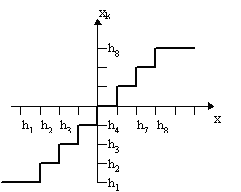
Цифровой сигнал описывается квантованной дискретной функцией x_k(nT), т.е. функцией, принимающей лишь ряд дискретных значений h₁, h₂, ... , h_M - так называемых "уровней квантования".    Последовательность x_k(nT) можно представить как результат преобразования последовательности x(nT) функцией квантования Ф_M(x)  x_k(nT)= Ф_M[x(nT)].    

Число уровней квантования M = 2^N, где N - число двоичных разрядов (бит) в представлении сигнала.    Цифровой сигнал тем точнее представляет соответствующий дискретный сигнал, чем больше уровней квантования и, соответственно, разрядов цифрового представления данных. Разность между квантованным и неквантованным сигналом e(nT)=x_k(nT) - x(nT) называется шумом квантования. Если записать последнее выражение как x_k(nT)=x(nT)+e(nT), то станет ясно, что в любой цифровой системе обрабатывается не "чистый" дискретный сигнал, а его смесь с шумом квантования.    Шум квантования равномерно распределен в интервале [0,h] (h=h_n-h_n-1 - шаг квантования), его дисперсия равна h²/12.   Шум квантования некоррелирован с сигналом и имеет постоянную спектральную плотность. Поэтому график типичного спектра гармонического сигнала, преобразованного с помощью АЦП в цифровую форму имеет вид, изображенный на рис.3.

Рис.2. Функция квантования

Рис.3.Графикспектра гармонического сигнала, преобразованного с помощью АЦП в цифровую форму. (Длина выборки выбрана кратной периоду сигнала).

Относительный уровень шумового пьедестала спектра определяется, естественно, разрядностью цифрового представления сигнала. Отношение сигнал/шум определяется как частное от деления мощности сигнальной компоненты спектра на сумму мощностей шумовых компонент спектра (равную дисперсии шума квантования) в полосе частот от нуля до половины частоты выборки.    

Подчеркнем: аналого – цифровое преобразование применимо только для одномерных сигналов (функций времени).

Однако, разработчикам цифрового телевидения, систем видеонаблюдения и других аналогичных систем приходится иметь дело с многомерными сигналами, преобразование которых требует применения соответствующих методов и средств обработки.

Дискретное преобразование Фурье

Одним из наиболее распространенных средств обработки как одномерных, так и многомерных сигналов, являются ортогональные преобразования. В цифровом телевидении, где задача уменьшения объема данных является одной из главных, роль указанных средств исключительно важна. Сущность ортогональных преобразований заключается в представлении исходного сигнала в виде суммы ортогональных базисных фунукций.

Функции x(t) и y(t) называются ортогональными на отрезке (t , t), если их скалярное произведение равно нулю, т. е.

[ 1 ]

Это определение может быть распространено на дискретные синалы, представляемые в виде чисел. Дискретные сигналы x(n) и y(n) имеющие по N отсчетов, по аналогии называются ортогональными, если выполняется условие

[ 2 ]

Наиболее известным примером ортогонального преобразования является разложение периодического сигнала x(t) в ряд Фурье

[ 3 ]

где ω₀ =2π / T; T – период повторения сигнала x(t).

Действительные коэффициенты ряда Фурье a_{k ,}b _k определяются соотношениями

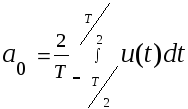[ 4 ]

[ 5 ]

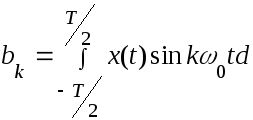[ 6 ]

В комплексной форме разложение в ряд Фурье имеет вид

[ 7 ]

где

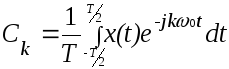[ 8 ] - комплексные амплитуды гармоник;

j – мнимая единица.

В ряд Фурье может быть разложен не только периодический сигнал, имеющий период Т, но и сигал, который отличается от 0 только на интервале времени (-Т/2, Т/2). В этом случае используется периодическое продолжение сигнала на всю ось времени с периодом Т.

Рассмотрим дискретный сигнал x(n)б отличный от нуля при n =0, 1, …, N-1. Для такого сигнала тоже можно ввести разложение по базису синусоидальных функций. Так как частотный спектр дискретизируемого сигнала должен быть ограничен сверху в соответствии с условием теоремы Котельникова, в разложении дискретного сигнала остается конечное число частотных составляющих, представляющих собой дискретные комплексные гармонические функции. Такое разложение, называемое дискретным преобразованием Фурье (ДФП), имеет вид

[ 9 ] n = 0,1,… , N-1,

где коэффициенты ДПФ X(k) определяются соотношением

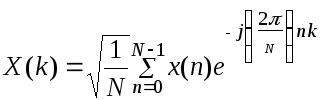[ 10 ] k=0,1,…,N-1.

Отметим, что нахождение коэффициентов по [ 10 ] называется прямым ДПФ, а получение сигнала по этим коэффициентам в соответствии с [ 9 ] - обратным ДПФ. В этих соотношениях появились суммы, так как исходный сигнал является дискретным. Частоте kω₀ , используемой в разложении аналоговых сигналов и имеющей размерность рад/с, в ДПФ соответствует безразмерная величина 2πk / N, где k = 0,1,…, N-1. Отношение k/N показывает, какую часть частоты дискретизации составляет частота данной дискретной гармоники.

Коэффициенты ДПФ X(k) и экспоненциальные множители в формулах [ 9 ] и [10 ] являются комплексными числами. Каждое комплексное число запоминается в цифровом ЗУ в виде пары действительных чисел, представляющих его действительную и мнимую части. Сложение комплексных чисел требует выполнения двух операций сложения действительных чисел – отдельно складываются действительные и мнимые части. Умножение двух комплексных чисел требует четырех операций умножения и двух операций сложения действительных чисел. Таким образом, выполнение ДПФ в комплексной форме приводит к существенному увеличению объема ЗУ и времени вычислений.

Дискретное косинусное преобразование.

Чтобы иметь дело только с действительными числами, обычно используют разложение с помощью дискретного косинусного преобразования(ДКП). Это преобразование описывается соотношением

[ 11 ]

где коэффициенты ДКП определяются по формулам

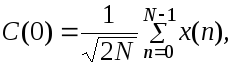
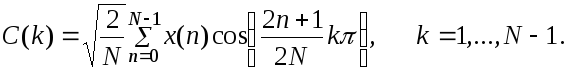[ 12 ]

Как и в случае ДПФ, нахождение коэффициентов C(k) по формуле [ 12 ] называется прямым ДКП, а представление сигнала в виде [ 11 ] называется обратным ДКП.

Аналогично можно записать соотношение для прямого и обратного ДПФ и ДКП в двумерном случае. Двумерный дискретный сигнал, например, отдельный кадр цифрового телевизионного сигнала, представляется матрицей значений x(m,n), где m = 0,…,M - 1 – номер отсчета в строке, n = 0,…, N - 1 – номер строки в кадре.

Прямое двумерное ДПФ имеет вид

[13 ]

k = 0,…,M – 1, l = 0,…,N – 1,

где X(k,l) – комплексные коэффициенты ДПФ, отображающие пространственно частотный спектр изображения.

Обратное двумерное ДПФ представляет разложение изображения по базисным функциям

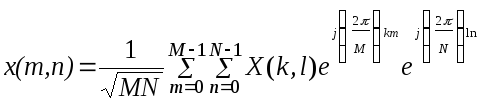. [ 14 ]

Коэффициенты двумерного прямого ДКП определяются по формулам

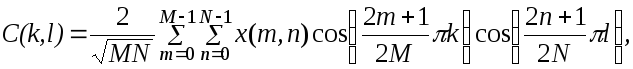
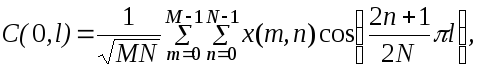
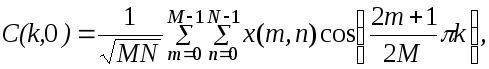
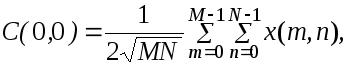[ 15 ] (все коэффициенты).

Обратное двумерное ДКП имеет вид

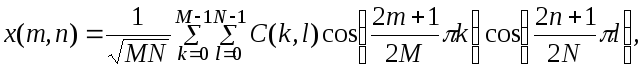[ 16 ]

Величины k / M l / N являются дискретными пространственными частотами, по горизонтальной и вертикальной координатам, соответственно, которые выражаются безразмерными величинами, имеющими такой же смысл, как и дискретная частота в одномерном случае. Каждая дискретная пространственная частота пропорциональна отношению пространственного периода дискретизации по данной координате к пространственному периоду этой частотной составляющей. Пространственные периоды при этом измеряются в единицах расстояния.

Оценим количество операций, необходимых для вычисления ДПФ в соответствии с формулой [ 10 ]. Дл я этого преобразуем это выражение, выделив в нем операции над действительными и мнимыми частями чисел

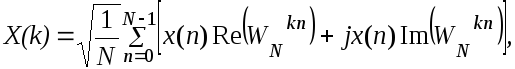[17]

где k = 0,…,N-1; .

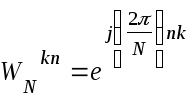При этом учитывается, что значения сигнала x(n) являются действительными числами.

Из [17] видно, что для вычисления одного значения X(k) необходимо выполнить приблизительно 2N умножений и 2N-2 сложений действительных чисел. Для вычисления всех N значений X(k) надо выполнить 2N² умножений и N(2N-2) сложений действительных чисел. Кроме того требуется ЗУ для хранения значений x(n), X(k) и W_N ^kn.

Выполнение обратного ДПФ потребует в два раза больше операций, так как значения X(k) являются комплексными числами, и количество слагаемых увеличится вдвое.

В целом можно оценить затраты вычислительных ресурсов при выполнении прямого и обратного ДПФ как пропорциональные N². Аналогично можно показать, что вычисление двумерных прямого и обратного ДПФ требует выполнения количества операций, пропорционального N² M²

Например, вычисление ДПФ для квадратного блока изображения, содержащего 8х8 элементов (пикселов), потребует выполнения примерно 16x10³ операций умножения и сложения. Время вычисления ДПФ для телевизионного кадра цифровым процессором с быстродействием 1 миллион операций в секунду составит около 200 часов. Вполне очевидно, что с одной стороны нужно повышать быстродействие процессора, а с другой искать пути уменьшения объема вычислений.

Одним из способов сокращения объема вычислений является применение открытых в 60 – х годах прошлого века алгоритмов ДПФ, называемых алгоритмами быстрого преобразования Фурье (БПФ). Существо решения, обеспечивающего выигрыш в количестве операций, заключается в использовании периодичности экспоненциальных функций типа

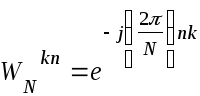
и их симметрии относительно перестановки множителей n,k.В наиболее простом случае, когда N = 2^r, где к – натуральное число, вычисление значения X(k) одномерного ДПФ разбивается на к шагов. На первом шаге отсчеты исходного сигнала x(n) разбиваются на пары и для каждой пары вычисляются коэффициенты ДПФ при N=2. На втором шаге по результатам первого шага находят коэффициенты ДПФ с N=4 для групп по четыре элемента и т.д. Аналогично выполняется вычисление обратного ДПФ.

На каждом шаге необходимо N комплексных сложений и N комплексных умножений. Число же шагов равно log₂N. Таким образом, число операций, которые необходимо выполнить для вычисления прямого или обратного ДПФ оказывается пропорциональным N log₂ N.

Другие приемы уменьшения объема вычислений.

Двумерное БПФ может быть разложено на последовательность одномерных. Число требуемых операций оказывается пропорциональным NM log₂ (MN). Для обработки телевизионного кадра при этом требуется примерно 8х10⁶ операций, что в 10⁵ раз меньше, чем число операций, требуемое для непосредственного вычисления ДПФ.

Существуют также быстрые алгоритмы вычисления ДКП. В цифровом телевидении основную роль играет ДКП блоков 8х8 пикселов, при выполнении которого используется алгоритм быстрого вычисления одномерного ДКП отрезк цифрового сигнала, содержащего восемь элементов. При этом сначала вычисляются ДКП для каждого столбца блока элементов изображения, а затем в полученной матрице 8х8 чисел вычисляются ДКП для каждой строки.

Таким образом, мы рассмотрели методы предварительной обработки информации в ТКС, их особенности и области применения. Изложенный материал является важным для изучения последующих разделов курса.

ЛИТЕРАТУРА.

1. Сергиенко А.Б. Цифровая обработка сигналов. М.:”ПИТЕР”, 2002 г.

стр.127 – 133.

2. Смирнов А.В. Основы цифрового телевидения. М.: “Горячая линия - Телеком“, 2001 г. стр. 13 – 29, 49 – 57.

12