05-11-2014_14-27-37 / Splaines

Сплайны. Примеры построения

Определение

Рассмотрим разбиение N отрезка [a, b]: a = x0 < x1 < ... < xN = b.

Sm,k (x) называется сплайном степени m с дефектом k (0 ≤ k ≤ m) и узлами N , если:

1) на любом частичном отрезке [xi, xi+1], i = 0, 1, ..., (N − 1), Sm,k многочлен степени ≤ m, и хотя бы на одном из отрезков степень равна m;

2) Sm,k C(m−k)[a, b], причём S(m−k+1)(x) не является непрерывной на [a, b].

m,k

Пример 1 Построение S1,1(x).

Пусть хотим построить S1,1(x) кусочно–линейную, непрерывную на [a, b] функцию, принимающую в точках xi значения yi (yi = S1,1(xi)).

Тогда на каждом [xi, xi+1] можно получить явную формулу для S1,1(x):

Рассмотрим функцию ϕ(x) = (1 − |x|)+ = max{0, 1 − |x|}.

Рассмотрим {ϕi(x)}Ni=0. Они образуют базис для сплайна S1,1(x), так как очевидно, что

1

Пример 2 Построение S3,2(x).

Пусть нужно построить кубический сплайн, дефекта 2. Это означает, что кроме непрерывности самой функции, необходимо соблюсти непрерывность её первой производной.

1) На каждом отрезке [xi, xi+1], i = 0, 1, ..., (N − 1) кубический сплайн S3,2(x) имеет вид ai · x3 + bi · x2 + ci · x + di. Таким образом, всего неизвестных параметров, подлежащих определению ровно 4N.

2) Условие непрерывности S3,2(x) и S3′ ,2(x) во всех внутренних узлах разбиения N даёт нам только (N − 1) · 2 = 2N − 2 условия. Для нахождения всех неизвестных

нужно задать недостающие 2N + 2 условия.

Зададим в каждом xi, i = 0, 1, ..., N значения yi и yi′ (всего 2N + 2 значения). Таким образом, на отрезке [xi, xi+1] ставится задача интерполирования Эрмита:

S3,2(xi) = yi, S3′ ,2(xi) = yi′.

Получим базисное представление сплайна S3,2(x). Пусть i = 0, 1, ..., (N − 1) (xi+1 − xi) = h > 0.

Рассмотрим функцию ϕ(x), заданную на [0, 1], такую что ϕ(0) = 1, ϕ(1) = 0, ϕ′(0) = ϕ′(1) = 0. Ясно, что ϕ(x) многочлен 3-ей степени. Можно получить для него явную формулу: ϕ(x) = 2x3 − 3x2 + 1.

Рассмотрим функцию ψ(x), также заданную на [0, 1], такую что ψ(0) = ψ(1) = 0, ψ′(0) = 1, ψ′(1) = 0. Снова имеем многочлен 3-ей степени. Явная формула для него: ψ(x) = x · (x − 1)2.

Заметим, что взяв линейную комбинацию αϕ(x) + βψ(x), можно добиться любого значения функции в 0 за счёт выбора α и за счёт выбора коэффициента β, получить любое значение производной в нуле.

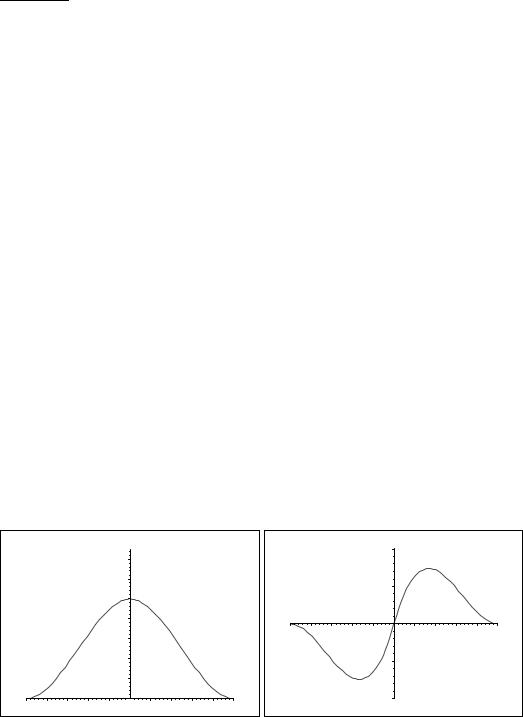
Далее, продолжим ϕ(x) чётно на [−1, 0], а ψ(x) нечётно на [−1, 0]. Вне отрезка [−1, 1] функции продлим нулём.

Ниже приведены графики функций ϕ(x), ψ(x) на [−1, 1].

N

S3,2(x) = (yi · ϕi(x) + h · yi′ · ψi′(x)).

i=0

2