Физика колебания и волны . лекция и вопросы / OF2_1_Kolebania_mini

2.1.9. Разложение сложных колебанийбаний..

Гармонический спектр сложного колебаниялебания

Вопрос о возможности разложения сложного колебания на простые (гармонические) колебания в общем виде был решён французским математиком и физиком Жаном Батистом Жозефом Фурьé (1768-1830), который доказал, что любая сложная периодическая функция может быть представлена суммой достаточно большого числа простых (гармонических) функций, периоды которых кратны периоду сложной функции.

Сложение взаимно перпендикулярных гармонических колебаний, при ω1 ≠ ω2

Согласно теореме Фурьé:

Любое сложное колебание может рассматриваться как результат сложения соответствующего числа простых (гармонических) колебаний, периоды или частоты которых кратны периоду или частоте сложного колебания.

Совокупность этих простых колебаний называют

гармоническим составом или гармоническим спектром данного сложного колебания. Гармонический спектр сложного колебания является его важнейшей характеристикой.

Релаксационные колебания

(Relaxation oscillations)

Среди сложных по форме колебаний различают один весьма важный для практики вид – релаксационные колебания. Это колебания, в которых обычно чередуются участки быстрых и медленных изменений состояния системы.

Накопительные колебания

Некоторое представление об одном из видов релаксационных колебаний, так называемых

накопительных колебаниях, может дать следующая модель. Сосуд равномерно наполняется водой из крана, при этом вода периодически выливается с помощью сифона, который быстро опорожняет сосуд, как только уровень h воды в нём достигнет высоты hm колена сифона. Уровень h воды в сосуде при этом совершает колебания, примерный характер которых показан на графике.

Пример накопительных колебаний: 1

– наполнение; 2 – опорожнение

Релаксационные колебания

(Relaxation oscillations)

В более широком смысле релаксационными называют колебания, график которых имеет несимметричную форму, значительно отличающуюся от синусоиды (прямоугольную, пилообразную и т.п.).

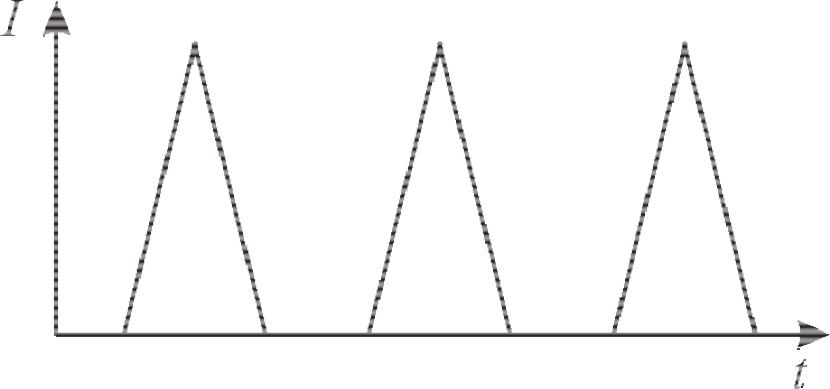
Колебания с импульсами треугольной формы

Колебания экспоненциальной формы

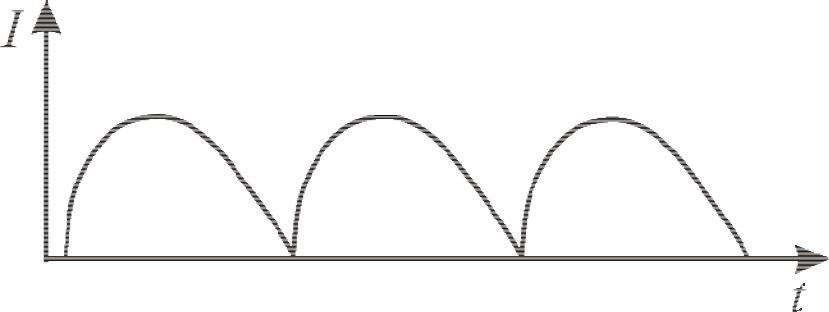
Диадинамические импульсные колебания

2.1.10. Математическийй ии физический маятникии

Маятник – твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси.

Математический маятник – материальная точка,

подвешенная на нерастяжимой невесомой нити с закреплённым другим концом и имеющая возможность под действием силы тяжести совершать колебания по дуге окружности относительно точки закрепления.