Приложение 2. Объяснение векторных символов и операций
1. Вектор это величина, которая характеризуется не только размерами, но и направлением. Чтобы отличить векторы от скалярных величин, первые будут обозначаться жирным шрифтом.
2. Пусть А – вектор, величина которого (модуль) ‑ |А|. Если вектор А спроектирован (ортогонально) на оси x, y, z прямоугольной системой координат, то получим компоненты Ax, Ay, Az, и, наоборот, вектор определяется тремя компонентами. Важно, что не любые наборы из трех скалярных величин являются компонентами вектора. Векторы описывают физические объекты, которые можно складывать по правилу параллелограмма.
Величина (модуль) вектора дается посредством равенства
,
(П2.1)
а направляющие косинусы его
,
,
.
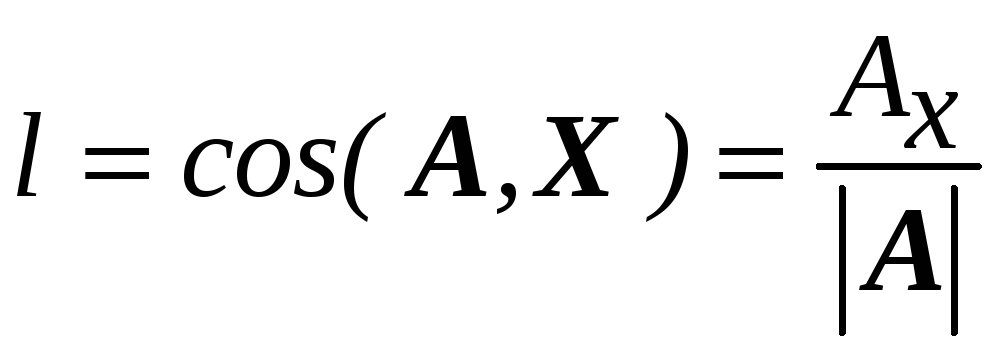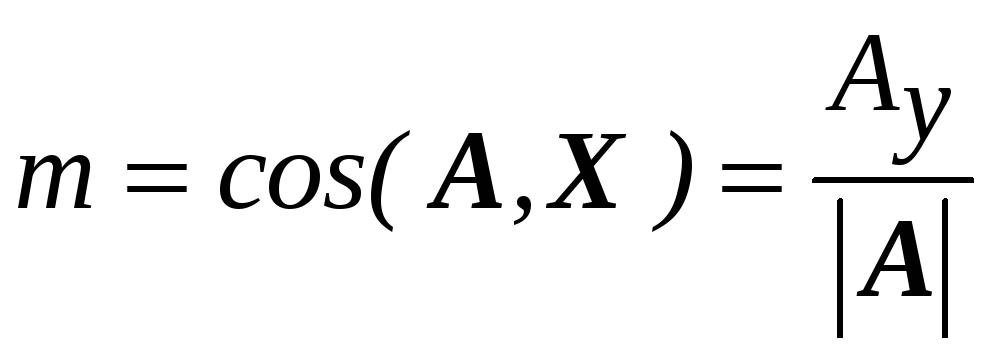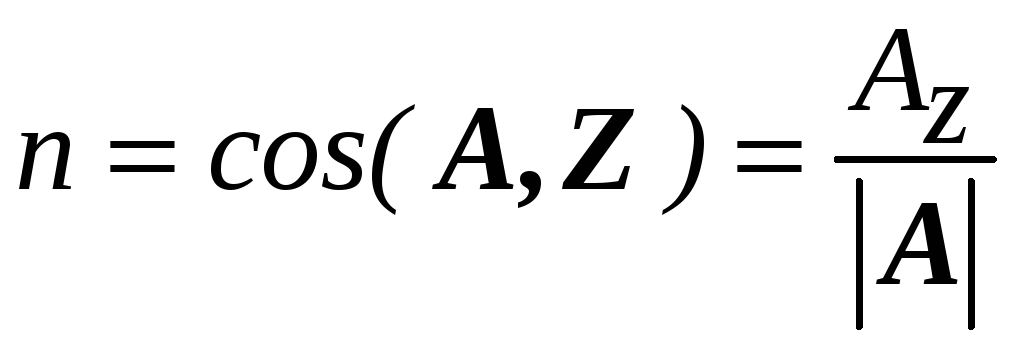(П2.2)
3. Произведение вектора А и скаляра α есть вектор, направление которого совпадает с направлением А, а величина в α раз больше А. Аналогично вектор А, умноженный на величину |A|-1, есть вектор единичной длины a, совпадающий по направлению с А. Следовательно,
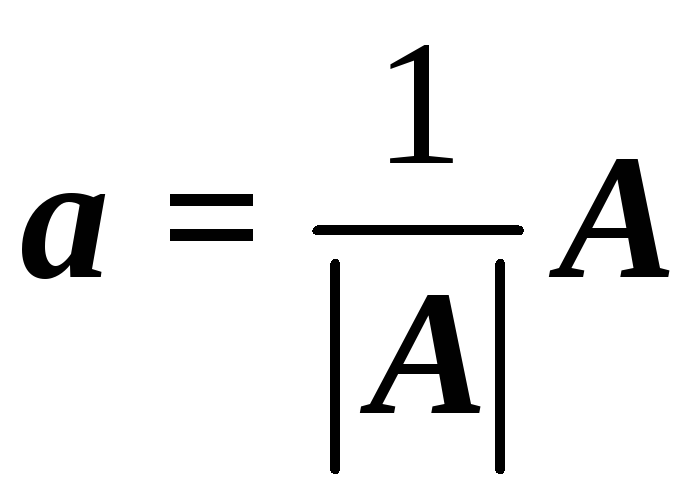(П2.3)
4. Пусть i, j, k, будут единичными векторами осей координат x, y и z соответственно. Вектор А, может быть записан как сумма трех составляющих векторов или в виде набора компонент.
.
(П2.4)
Если В – другой вектор, можно написать таким же способом
.
(П2.5)
5. Сумма двух векторов А и В равна
,
(П2.6)
Из уравнения (П2.6) очевидно, что
(П2.7)
6. Скалярное произведение двух векторов А и В является скалярной величиной и обозначается точкой между ними и определяется как
,
(П2.8)
где β – угол между вектором А и вектором В. Поскольку знак cos β не зависит от знака β, то из уравнения (П2.8) следует, что в скалярном произведении порядок величин несущественен. Поскольку единичные векторы координатных осей направлены под прямым углом друг к другу, из вышеперечисленных определений следует, что
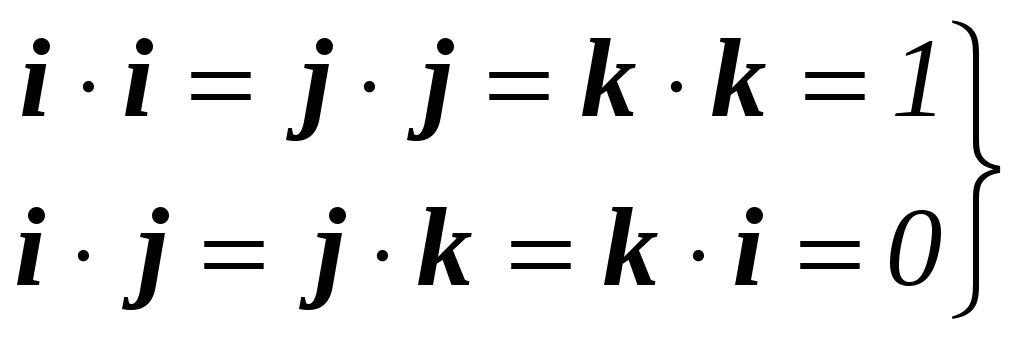(П2.9)
Умножая А на В в том виде, в каком они даны уравнениями (П2.4) и (П2.5), и используя уравнение (П2.9), получим выражение скалярного произведения векторов через их компоненты
,
(П2.10)
Если вектор В есть сумма, скажем
двух векторов В1
и В2 имеем следствие
.
7. Векторное произведение двух векторов А и В определяется как вектор С с модулем АBsinβ и направлением, перпендикулярным плоскости, проходящей через А и В так, чтобы вращающийся вправо винт, который поворачивал бы А (первый вектор) к В (второй вектор) и перемещался (ввинчивался) в направлении С. Отсюда следует, что величина векторного произведения А на В равна площади параллелограмма, построенного на векторах А и В как на сторонах. Чтобы отличить векторное произведение от скалярного используется знак умножения.
.
(П2.11)
Порядок векторов в векторном произведении
важно соблюдать, так как из определения
видно, что
и, следовательно,
.
(П2.12)
Если вектор В есть сумма двух векторов В1 и В2, то
(П2.13)
Единичные векторы координатных осей направлены под прямыми углами друг к другу, поэтому из уравнения (П2.11) и определения единичного вектора следует, что
,
,
,
.
(П2.14)
Умножая уравнение (П2.4) и (П2.5) и используя (П2.14), получим покомпонентное выражение для векторного произведения
,
(П2.15)
Его можно записать как символический детерминант
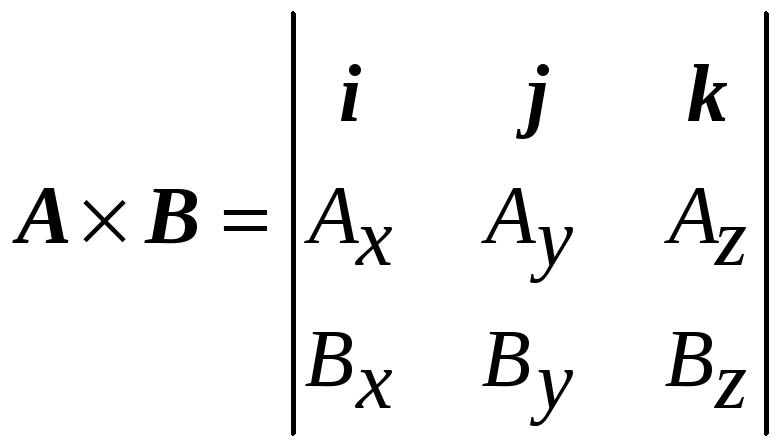(П2.16)
8. Умножение, включающее три вектора,
может быть осуществлено путем
последовательного использования
операций (П2.10), (П2.15) или (П2.16). Рассмотрим
сперва скалярное произведение вектора
А и другого вектора, который
является векторным произведением В
и С, т. е.
.
Поскольку А·В есть скаляр и
векторное умножение скаляра на вектор
не было определено, очевидно, что сперва
В должно быть векторно умножено
на С, а полученный в результате
вектор – скалярно умножен на А.
Написав векторы А, В и С
в форме (П2.5) и осуществив умножение в
указанном порядке, найдем, что
,
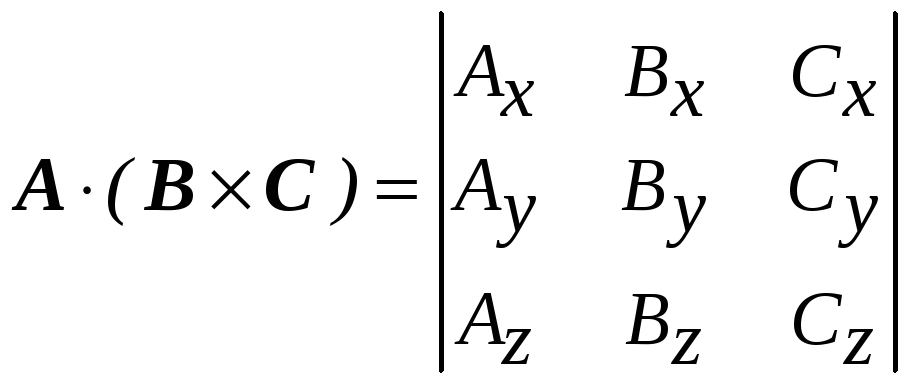(П2.17)
которое представляет собой скаляр, равный объему параллелепипеда со сторонами А, В и С. Из уравнения (П2.17) легко видеть, что
.
(П2.18)
Следовательно, в скалярно-векторном произведении векторы могут циклонически переставляться.
Рассмотрим затем векторное произведение
вектора А и другого вектора,
который является векторным произведением
двух векторов В и С,
.
Осуществляя векторное умножение внутри
скобок и затем векторное умножение
вектора А на результат первого умножения,
используя уравнение (П2.15) или (П2.16),
получим
.
(П2.19)
Это правило полезно и его легко запомнить,
используя мнемонику «бац минус цаб».
Вычисляя тем же способом тройное
векторное произведение
,
найдем, что
.
(П2.20)
Отсюда ясно, что порядок векторно-векторного умножения важен и скобки должны быть сохранены, чтобы указывать последовательность операций.
9.Дифференцирование вектора по параметру. Если вектор является переменным, зависящим от параметра, например от времени, то обычным образом определяется его производная по этому параметру
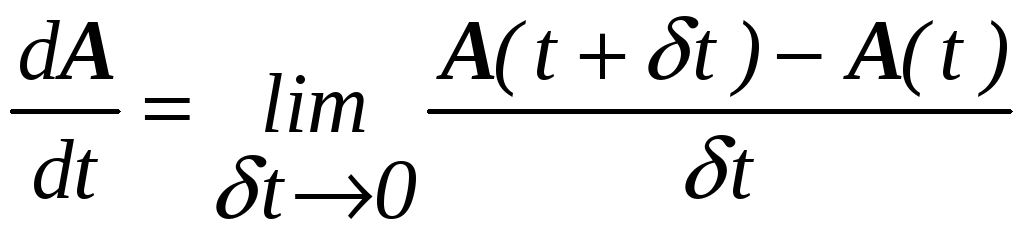(П2.21)
Разложив вектор A(t) по трем осям неподвижной координатной системы, можно показать, что дифференцирование вектора сводится к дифференцированию его компонент
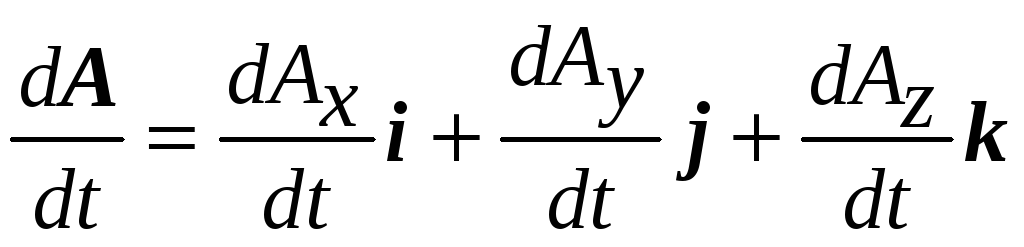(П2.22)
Известные правила дифференцирования произведения обобщаются на случай дифференцирования произведения скалярной функции на вектор, а также и на случаи дифференцирования скалярного и векторного произведений векторов. Поэтому справедливы формулы
(П2.23)
(П2.24)
(П2.25)
В формуле (П2.25) порядок сомножителей важен!
Если некоторая точка движется по кривой, то ее радиус-вектор r зависит от времени t. Дифференцируя r(t), получим вектор скорости v(t), а повторное дифференцирование дает вектор ускорения a(t).
,
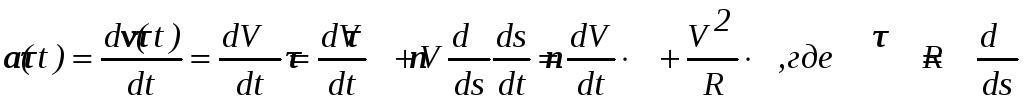.(П2.26)
В этих формулах использовано представление вектора скорости в виде модуля скорости V, умноженного на вектор направления касательной к траектории τ .Вектор τ является единичным, что доказывается в курсе дифференциальной геометрии. Дифференцируя его скалярное произведение на себя можно получить формулу
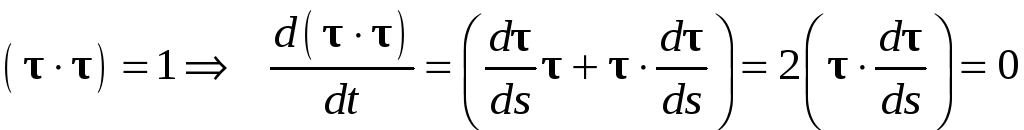(П2.27)
Она показывает, что вектор
перпендикулярен вектору касательной
τ. Однако его модуль равен
не единице, а кривизне траектории.
Поэтому единичным является только
вектор
, в котором R - радиус
кривизны траектории. Таким образом
формула (П2.26) показывает, что вектор
ускорения раскладывается на касательное
ускорение (изменение модуля скорости)
и нормальное (центробежное) ускорение.
10. Скалярное поле и градиент. В то время как вектор характеризуется величиной и направлением, скаляр характеризуется только величиной. Поле любого такого скаляра f(x, y, z) может быть представлено системой эквискалярных поверхностей или поверхностей уровня, вдоль которых f постоянно.
Изменения f на единицу
расстояния вдоль координатных осей
будут
,
,
(
в дальнейшем иногда употребляются и
обозначения
),
а изменения на единицу расстояния вдоль
нормали n к эквискалярной
поверхности f будут
.
Если n – единичный
вектор нормали к f-поверхности
и направлен от низких к высоким значениям
f, то вектор n
определяет пространственное измерение
f как по величине, так
и по направлению. Этот вектор называется
градиентом f и часто
записывается как gradf,
следовательно
.
Удобно ввести дифференциальный оператор
,
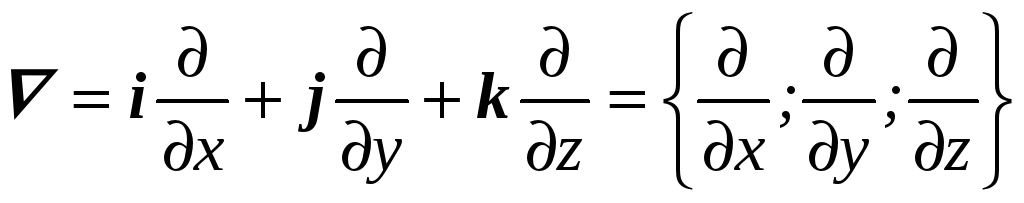(П2.28)
где, как и раньше, i, j и k – единичные векторы координатных осей.
Оператор
(его
называют оператором Гамильтона,
набла-оператором, наблой, или оператором
градиента) формально является
вектором и обозначает дифференцирование
в пространстве. Символическое произведение
оператора
и
скалярной величины f
определяется как
.
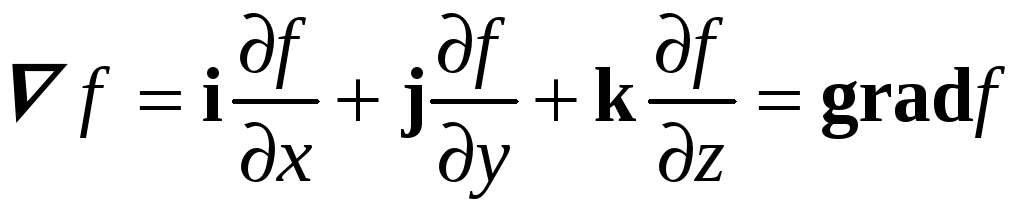(П2.29)
Преимущества использования оператора
заключаются в том, что дифференциальные
операции могут осуществляться согласно
правилам векторной алгебры и записываются
очень компактно.
11. Векторное поле, дивергенция и вихрь.
Пусть В – вектор, компоненты
которого являются функциями x,
y, z. Следовательно,
,
,
.
Эти три скалярные величины определяют
направление и величину вектора В
в каждой точке рассматриваемого
пространства. Вектор В может
быть записан как векторная функция x,
y, z
и представляет собой векторное поле,
если каждой точке соответствует
единственный набор компонент
вектора. Дифференциальные свойства
этого поля могут быть выражены посредством
оператора
.
Скалярное произведение
и вектора В получается из
уравнения (П2.10) путем замены А
на
и называется дивергенцией вектора
B т. е.
(П2.30)
Если, в частности, В ‑ вектор скорости V с компонентами u, v и w, имеем выражение
,
(П2.31)
которое характеризует расширение единичного объема частицы сплошной среды за единицу времени.
Векторное произведение
обозначается rotB,
оно обычно называется вихрем и
получается из уравнения (П2.15) или (П2.16)
посредством замены А на
т. е.
,
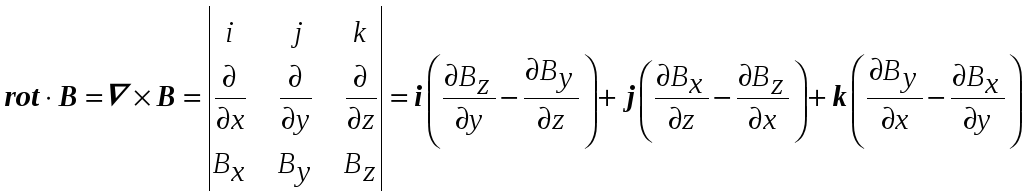(П2.32)
Обозначая вектор вихря скорости через ω, получим компоненты вектора вихря скорости
,
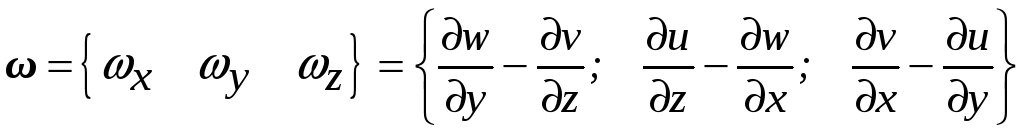(П2.33)
Вектор ω равен удвоенной угловой
скорости движения элемента объема
вокруг своей мгновенной оси вращения.
Особенно часто в метеорологии встречается
вертикальная составляющая вихря
скорости, которая зависит только от
компонент скорости ветра
.
Если, в частности, векторное поле
представлено посредством векторного
произведения двух векторов В и
С, то дивергенция является
смешанным скалярно векторным произведением
и посредством замены А на
в
уравнении (П2.17) получается
,
(П2.34)
Аналогично из уравнения (П2.19) получается формула для вихря от векторного произведения
,
(П2.35)
и формула для градиента скалярного произведения
,
(П2.36)
c важным частным случаем при B=C
,
(П2.37)
При выводе этих выражений важно заметить,
что оператор набла
действует на оба вектора внутри скобок.
12. Оператор
может быть использован повторно.
Здесь достаточно рассмотреть некоторые
простые комбинации. Заменяя вектор В
в уравнении (П2.30) на
f
и осуществляя умножение, легко найдем,
что
.
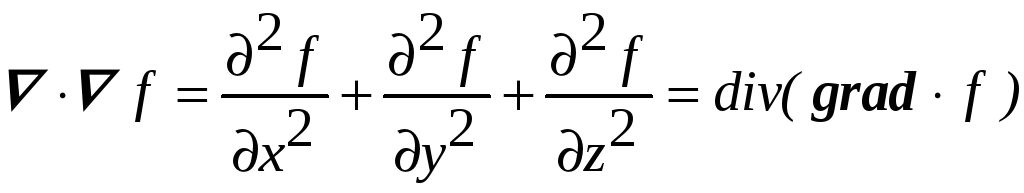(П2.38)
Выражение
f
обычно записывается в виде
.
(П2.39)
Оператор
,
или
,
называется оператором Лапласа. Он
имеет самостоятельное обозначение Δ
и называется лапласианом поля f.
Векторное поле, являющееся градиентом скалярного называется потенциальным, а сам скаляр, градиент которого порождает это векторное поле, называется потенциалом.
Если В в уравнении (П2.25) заменить
на
,
то получится формула
,
(П2.40)
Из нее следует. что вихрь градиента
скалярного поля равен нулю. Любое
векторное поле В, которое
удовлетворяет условию rot
B=0 (такие поля
называют безвихревыми), может быть
считать градиентом некоторого скалярного
поля f и записать в
виде В=
f.
Скалярная функция, с помощью которой
порождается безвихревое векторное
поле, называется потенциалом. Лапласиан
потенциала в соответствие с (П2.39) и
(П2.40) равен нулю.
Заменяя В в уравнении (П2.23) на rot В, легко получить, что
,
(П2.41)
Это значит, что дивергенция вихря равна нулю. Поэтому любое векторное поле В, которое удовлетворяет условию divB=0, может быть записано B=rot A. Такие поля называются соленоидальными, а вектор A в нем называют векторным потенциалом.
13. Полезные формулы для дифференцирования
векторного поля Если
,
то дивергенция такого поля имеет вид
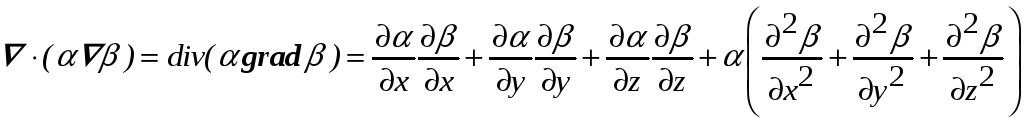(П2.42)
Используя вектора, её можно записать в виде
.
(П2.43)
Вихрь векторного поля
получается, если оператор
векторно умножается на
.
Он имеет вид:
, (П2.44)
поскольку
.
14.Теоремы Остроградского и Стокса. Поток и циркуляция вектора. Всякое векторное поле порождает скалярное поле дивергенции. Если в непрерывном и дифференцируемом векторном поле A выделить с помощью поверхности S некоторый объем V, то справедлива теорема Остроградского. Она имеет вид
. (П2.45)
Левая часть представляет собой интеграл от дивергенции по объему (см. формулу (П2.31)), а в правой части записан интеграл по поверхности от скалярного произведения вектора на направленный элемент поверхности, определяемый как вектор с составляющими
(П2.46).
Интеграл
называется потоком вектора A
через поверхность S.
Всякое векторное поле порождает также и векторное поле вихря. Поток вектора вихря через поверхность S можно вычислить по теореме Стокса
.
(П2.47)
Левая часть представляет собой поток вектора вихря вектора A через площадку S (см. формулу(П2.32)), а в правой части записан интеграл по контуру L, ограничивающему эту площадку, от скалярного произведения вектора на направленный элемент дуги кривой L. Последний представляет собой вектор, имеющий составляющие
(П2.48)
Интеграл
называется циркуляцией вектора по
контуру L.
Для обоснования формул термодинамики и других приложений полезно выделить случай расчета циркуляции потенциального поля. Подставляя вместо A в выражение для циркуляции градиент потенциала f, можно получить под знаком контурного интеграла полный дифференциал. Отсюда следует формула
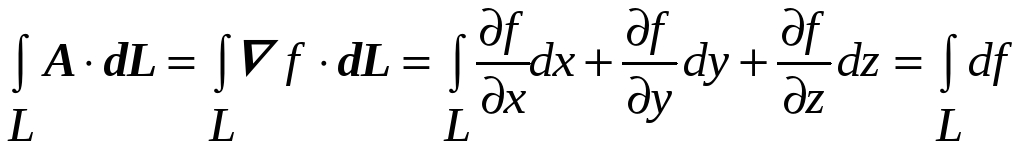(П2.49)
Понятно, что интеграл от потенциального вектора по контуру равен разности потенциалов между концом и началом контура, а по замкнутому контуру циркуляция потенциального вектора равна нулю.
15 Дифференцирование, следуя движению, или индивидуальная производная по времени. Если α такое скалярное поле, что α=α(x, y, z, t), то получим, дифференцируя, следуя движению, индивидуальную производную по параметру t, обозначающему время.
,
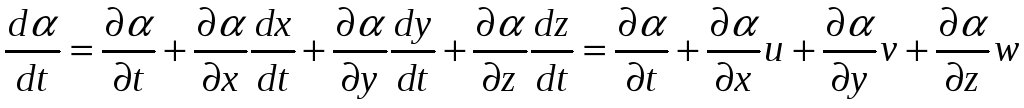(П2.50)
Здесь
,
и
являются скоростями изменения координат
движущейся выделенной частицы и,
следовательно, равны компонентам u,
v и w скорости
движения V. Это
выражение более коротко можно записать
в векторной форме
(П2.51)
Оператор индивидуальной производной
,
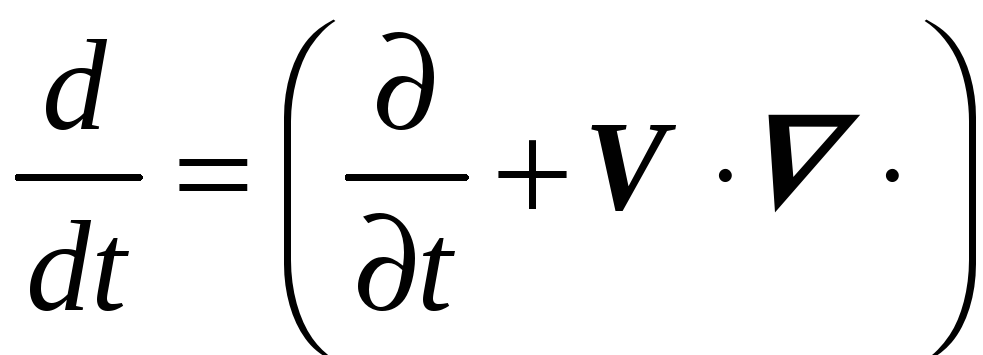(П2.52)
может быть также применен и к векторным величинам, если считать, что он действует на каждый из компонентов. Тогда для любого векторного поля А вместо трех скалярных равенств можно записать одно векторное
.
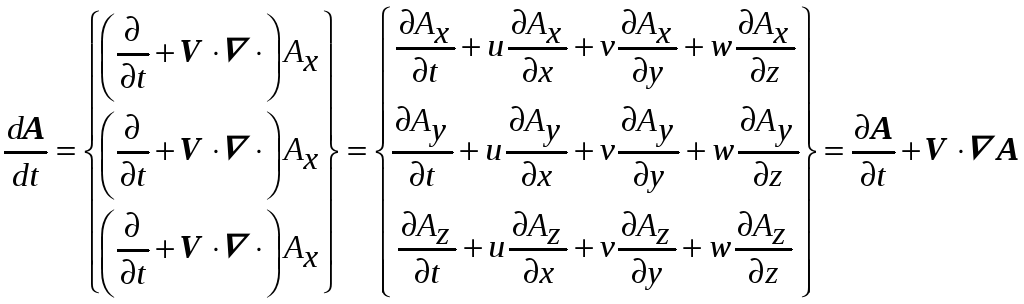(П2.53)
16.Графическое изображение векторного поля производится путем построения векторных линий. Векторная линия любого векторного поля B(x,y,z) – это линия, в каждой точке которой направление касательного вектора dr совпадает с направлением вектора рассматриваемого поля. Математическим определением векторной линии является равенство нулю векторного произведения
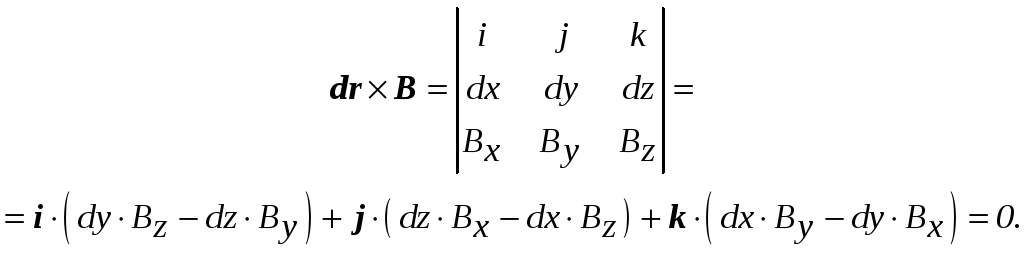(П2.54)
Оно выражает условие параллельности этих векторов. Приравнивая каждую компоненту равного нулю вектора к нулю, эти равенства можно преобразовать сначала к виду
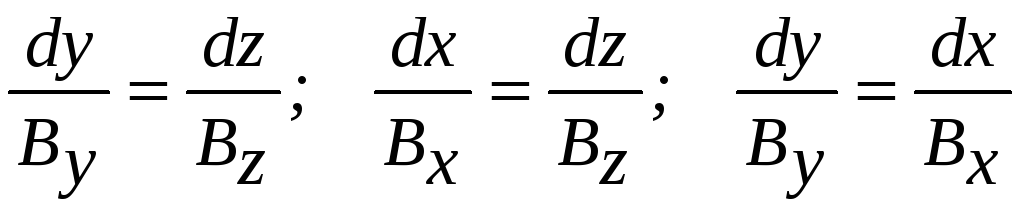(П2.55)
А затем к общепринятому виду уравнений векторных линий
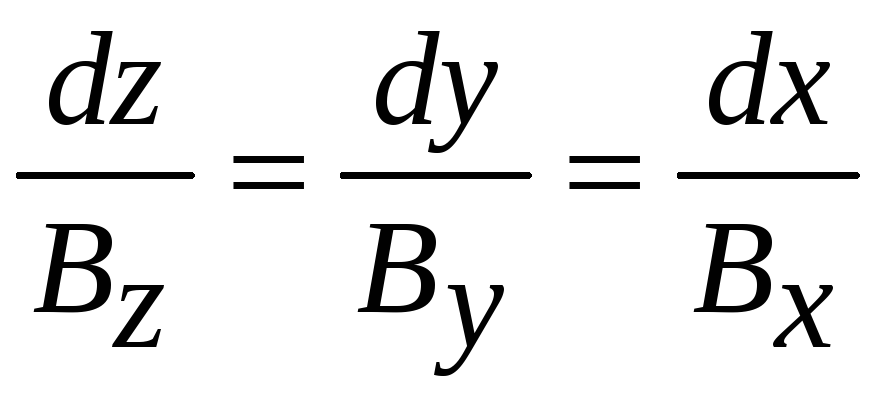(П2.56)