
Лабораторная работа № 4 Приближение Борна в задаче рассеяния электрона
Если потенциал U0и радиусaрассеивающего центра имеют не слишком большие значения, то можно найти приближенное решение интегрального уравнения (7). Как показывается в теории квантового рассеяния, условия для приближенного решения имеют вид.

Если выполняются условия, приведенные выше, то для получения приближенного решения в интеграле (7) вместо искомой функции lнадо подставитьjl.
![]() (16)
(16)
Такое приближение называют приближением Борна. Так как выбранная потенциальная энергия имеет простой вид
 (17)
(17)
то интеграл в выражении (16) можно вычислить аналитически.
Подставляем (17) в формулу (16). В результате интеграл в (16) принимает вид.
![]() (18)
(18)
Здесь для разных значений радиуса rвозникают две формулы:
Для raполучаем следующую формулу

Используя явный вид сферической функции Ханкеля (8), получаем
 (19)
(19)
Для raполучаем другую формулу
 (20)
(20)
Здесь интегралы I1,I2вычисляются по известным формулам, которые можно найти в пакетеMathematica. Для интегралаI1имеется простая формула
![]() (21)
(21)
Чтобы вычислить интеграл I2надо немного потрудиться
 (22)
(22)
Интеграл Aвычисляется аналогично интегралу (21)
![]() (23)
(23)
Для интеграла Bполучается следующее выражение
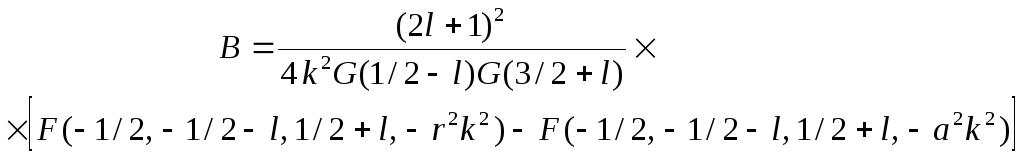 (24)
(24)
Здесь G(z) –гамма функция, в пакете она обозначаетсяGamma[], функцияF(,,,z) называется гипергеометрическая функция и в пакете обозначается как
HypergeometricPFQ[{}, {,},z]
В результате нам удалось получить аналитическое выражение для интеграла (18). Теперь, используя формулы (6), (7) можно найти волновую функцию электрона в задаче рассеяния на сферическом потенциальном барьере
![]() (24)
(24)
Задание 1.
Ряд для волновой функции (24) очень похож на ряд для плоской волны. Например, при U0= 0 они совпадают.
Задание будет состоятьв следующем. С помощью формулы (24) надо создать функциюMypsi[a,U0,k,z,]. Надо использовать аналогичные выражения для плоской волныMyexp[k,z,].
Первое, в ряде (24) вместо jl(kr) надо поставитьjl(kr) –I(a,U0,k,r).
Второе, число членов ряда Lдля случаяr<a, надо выбирать по формулL=(kr) +, а для случаяr>a, по формулеL=(ka) +.
Для полученной функции Mypsi[a,U0,k,z,] построить 3Dповерхность в области
–a z 3a, –2a 2a. Так как функцияMypsi[] комплексная, то интересно построить распределение плотности вероятности, т.е. надо строить поверхность для функции
Abs[Mypsi[]]^2. Далее надо построить линии уровня функцииAbs[Mypsi[]]^2.
Параметры задачи a,U0,kдолжны выбиться из условия применимости приближения Борна. Типичные значения параметров следующие
< a < 2 (нм)
0 < U0 < 0.1 (эВ)
0.1 < k< 5 (1/нм)
На следующем рисунке приведен пример для a= 2,U0= 0.02,k= 1.5.


Рис. 14
Красным кругом обозначено расположение центра рассеивания.
Ниже приводятся варианты выполнения лабораторной работы 4.
-
Варианты
a
U0
k
1
0.5
0.05
1.25
2
1
0.05
1.25
3
1.5
0.05
1.25
4
2
0.05
1.25
5
0.5
0.1
1.25
6
1
0.1
1.25
7
1.5
0.1
1.25
8
2
0.1
1.25
9
0.5
0.05
1.75
10
1
0.05
1.75
11
1.5
0.05
1.75
12
2
0.05
1.75
13
0.5
0.1
1.75
14
1
0.1
1.75
15
1.5
0.1
1.75
16
2
0.1
1.75
17
0.5
0.05
2
18
1
0.05
2
19
1.5
0.05
2
