2. Задание на выполнение лабораторной работы 5. Нахождение волновых функций дискретного спектра энергии гетероструктуры.

Для нахождения волновой функции соответствующей стационарному уровню E, необходимо вычислить амплитуды A_n, B_n волновой функции по формулам (24), (25). Чтобы воспользоваться формулами (24), (25) надо уметь вычислять матрицы переходов M_n и векторы L и R по формулам (13), (16), (18). Ниже приводится часть кода для вычисления этих матриц и векторов.

Амплитуды A_n, B_n волновой функции удобно задать одним списком, где нечетные компоненты будут соответствовать амплитудам A_n , четные амплитудам B_n . Ниже приведен код нахождения амплитуд.

Теперь по формулам (7), (8), (9) можно найти волновую функцию для данного уровня энергии. Ниже приводится соответствующий код.

Найденные волновые функции, вообще говоря, не нормированы на единицу.

Пусть интеграл от функции равенС.

Тогда легко проверить, что функция будет нормирована на единицу. Поэтому для каждой волновой функциинадо найти нормировочный множитель. После этого новая волновая функциябудет нормирована не единицу.

Ниже приводится код нахождения нормировочных множителей волновых функций для всех дискретных уровней гетероструктуры.

Теперь опишем алгоритм построения волновой функции, например второго уровня. Из списка уровней энергии берем второй элемент.

Для данной энергии находим все амплитуды волной функции.

Берем нужный нормировочный множитель Na[[2]] , и строим график этой волновой функции.

Результат показан на рисунке 5.

Рис. 5

Следующий код позволяет построить графики всех волновых функций в цикле, вывести каждую волновую функцию по отдельности и все вместе.

Ниже показан результат работы программы.

Рис. 6 Энергия уровня

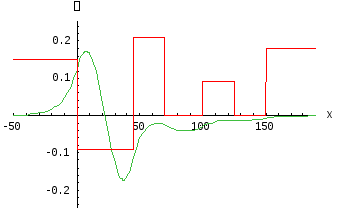
Рис. 7 Энергия уровня

Рис. 8 Энергия уровня

Рис. 9 Энергия уровня

Рис. 10 Энергия уровня

Из рисунков видно, что волновые функции подчиняются правилу общему для одномерных решений уравнения Шредингера. Волновая функция основного состояния не имеет узлов. Волновая функция первого возбужденного состоянияимеет один узел. Следующая волновая функцияимеет два узла. И, наконец, функцияимеет четыре узла. Это правило удобно использовать для проверки правильности найденного решения.

На следующем рисунке приведены все волновые функции вместе.

Рис. 11

3. Задание на выполнение лабораторной работы 5. Нахождение дискретного спектра и волновых функций гетероструктуры данной в варианте.

Пусть гетероструктура состоит из двух ям и барьера между ними. Параметры такой гетероструктры для каждого варианта приведены в таблице. Необходимо для своего варианта написать программу аналогичную рассмотренной выше. Найти все уровни дискретного спектра гетероструктуры и все волновые функции.

Таблица параметров гетероструктуры

Варианты	UL	U1	U2	U3	UR	d1	d2	d3
1	0.5	-0.3	0.7	0.0	0.6	45	25	40
2	0.4	-0.3	0.5	0.0	0.4	45	35	40
3	0.5	0.0	0.5	-0.3	0.5	35	35	35
4	0.5	0.0	0.5	0.3	0.5	35	35	35
5	0.5	0.0	0.5	0.3	0.5	20	40	40
6	0.5	0.0	0.5	0.0	0.5	20	40	40
7	0.5	0.0	0.5	0.0	0.5	10	50	50
8	0.4	0.0	0.65	0.0	0.5	30	40	40
9	0.4	0.0	0.15	0.0	0.5	30	40	40
10	0.4	-0.3	0.10	-0.2	0.3	50	40	40
11	0.4	-0.3	0.6	-0.2	0.3	50	40	40
12	0.4	-0.3	0.6	-0.2	0.3	20	50	40
13	0.3	-0.3	0.6	-0.2	0.3	10	50	50
14	0.6	0.0	0.45	-0.15	0.3	45	45	45
15	0.6	0.0	0.45	-0.15	0.15	45	45	45
16	0.2	0.0	0.45	0.0	0.2	45	50	35
17	0.2	-0.2	0.45	0.0	0.2	45	50	35
18	0.2	-0.2	0.45	0.1	0.2	45	50	35
19	0.2	-0.1	0.5	-0.1	0.15	40	50	60
20	0.3	0.0	0.8	0.0	0.3	30	10	70
21	0.1	0.0	0.8	0.0	0.3	50	10	70
22	0.4	0.0	0.4	-0.2	0.3	50	40	30
23	0.3	-0.2	0.1	-0.2	0.3	50	40	30
24	0.3	0.0	0.2	0.0	0.3	50	40	30
25	0.15	0.0	0.2	0.0	0.3	50	35	30