Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский Государственный Технический Университет им. П.О. Сухого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика АВАКЯН / posobie1

.pdf

Скачиваний:

Добавлен:

15.04.2015

Размер:

4.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 214 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

некоторому правилу или закону поставлено в соответствие									xn , то
говорят, что задана последовательность xn .
, , , … , , … , , …									(3.2)
1 2	3						′
Например:
	1		1		1		1
		1,		,		,...,		,...	(3.3)
		1,		,		,...,		,...	(3.3)
n			2		3		n

Определение 1. Число a называется пределом последовательности, если для любого сколь угодно малого положительного найдется такой номер N , что для всех n N выполняется неравенство:

xn a		.	(3.4)

Тот факт, что число a является пределом последовательности xn , записывается так:

		lim xn a .			(3.5)
		n
Неравенство	(3.4) эквивалентно неравенствам			xn	a	или
a xn a . Последние неравенства			означают, что		элемент	xn
находится в - окрестности числа a .			- окрестностью числа a
называется	интервал	a , a . Поэтому		определение предела

последовательности можно сформулировать также и следующим образом:

Определение 2. Последовательность xn имеет предел, если существует число a такое, что в любой - окрестности числа a находятся все элементы последовательности xn , начиная с некоторого номера.

Теоремы о пределах последовательности

Теорема 1. Если последовательность имеет предел, то он единственный. Теорема 2. Если последовательность имеет предел, то она ограничена. Теорема 3. Предел суммы (разности) двух последовательностей

равен
сумме (разности) пределов этих последовательностей.
lim xn yn lim xn lim yn .
n	n	n

Теорема 4. Предел произведения двух последовательностей равен
произведению пределов этих последовательностей.
lim xn yn	lim xn	lim yn .
n	n	n

Теорема 5. Предел частного двух последовательностей равен частному пределов этих последовательностей (при условии, что знаменатель не обращается в нуль).

lim xn

lim

;

lim

n yn

lim yn

Теорема 6. Если для двух последовательностей

lim x

a и

lim yn a ,

члены последовательности

удовлетворяют неравенству

xn zn yn , тогда lim zn a .

Приведем

несколько

примеров

вычисления

пределов

последовательности.

Пример 3.1

Вычислить предел последовательности xn 2n 1 n 3 3n 5 .

2n 3

Решение:

В данном примере последовательность представляет собой рациональную дробь, для вычисления пределов такого вида необходимо

знаменатель и числитель дроби разделить на n в наивысшей степени. В

нашем примере это n 3 .

2n 1 n 3 3n 5

lim

2n 3

n 3

1 3

lim

Так как

0, если n , а c - ограниченная величина.

Ответ: limn 2n 1 n 3 3n 5

2n3

Пример 3.2

Вычислить предел последовательности xn

3 3n 3 10

Решение:

Аналогичный прием во многих случаях можно применять и для дробей, содержащих иррациональности.

													n
			n
lim			n				lim						n
													n

			3	10								3
n 3	3n		3					n			3n	3		10
	3n								3		3n			10
									3
											n3			n3
lim				1					1	.
								3

n		3			10				3
	3				10				3
	3					n3
						n3

Ответ: lim

n 3

Пример 3.3

Вычислить предел последовательности xn

n 1 n .

Решение:

Для вычисления

подобных пределов

с неопределенностью ,

необходимо

умножить и разделить

xn на

его сопряженное. Это

необходимо для того, чтобы воспользоваться формулой «разность

квадратов»

a 2 b2

a b a b

и,

избавившись

от квадратного

корня, получить дробь.

) lim

n 1

lim (

n 1

lim

n 1

Ответ: lim (

n 1

n) 0.

Пример 3. 4

Вычислить предел последовательности

n n 1

Решение:

Для вычисления подобных пределов необходимо умножить и разделитьxn на неполный квадрат суммы. Это необходимо для того, чтобы

воспользоваться формулой «разность кубов»

a 3 b3 a b a 2 ab b2 и, избавившись от кубических корней,

получить дробь. Неполным квадратом суммы в нашем примере является: 3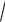n4 3n2 3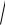n n 1 3n2 n 1 2 .

lim 3

n(n 1)

n2 n 1 2

lim

n n 1

3 n

3 n2 n 1 2

3 n4 3 n2 3

n n 1

n2 n n 1

lim

n 3 n4 3 n2 3

n n 1

3 n2 n 1 2

lim

3 n4

n 3 n4 3 n2 3

n n 1

3 n2 n 1 2

lim

1 3 1

3 1

Ответ: lim 3

n(n 1)

Пример 3.5

Вычислить предел последовательности xn 1 2 3 ... n . n 2

Решение:

Последовательность 1,2,3,..., n - является арифметической прогрессией с разностью d 1. Сумма n первых членов арифметической прогрессии находится по формуле:

(3.6)

Т.е. Sn

1 n

n n 2

, тогда

n n 2

1 2 3 ... n

n n 2

lim

n 2

2 n

Ответ: lim

1 2 3 ... n

Пример 3.6

3n 1 ! 3n 1 ! .

Вычислить предел последовательности xn

3n ! n 1

Решение:

Напомним, что

n! 1 2 3... n

(3.7)

			n 1 ! n 1 n!
lim	3n 1 ! 3n 1 ! lim 3n 1 ! 3n 1
n		3n ! n 1	n		3n 3n 1 !
lim		1 3n 1 3n	lim	9n2	3n 1	3.
		3n n 1
n			n	3n2 3n
Ответ: lim 3n 1 ! 3n 1 ! 3.
n	3n ! n 1

(3.8)

3n 3n 1 !

n 1

§ 3.2. Бесконечно малые и бесконечно большие величины

Определение 3. Последовательность

если lim xn 0. Последовательность

большой, если lim xn .

называется бесконечно малой,называется бесконечно

Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

Произведение конечного числа бесконечно малых величин есть величина бесконечно малая.

Произведение конечной величины на бесконечно малую величину есть величина бесконечно малая.

Сумма конечного числа бесконечно больших величин есть величина бесконечно большая.

Произведение конечного числа бесконечно больших величин есть величина бесконечно большая.

Произведение конечной величины на бесконечно большую величину есть величина бесконечно большая.

Если xn является бесконечно большой величиной, то ее обратная

величина n 1 xn будет бесконечно малой.

§ 3.3. Предел последовательности 1 +	1
§ 3.3. Предел последовательности 1 +		. Число

Предел данной последовательности равен

	1
lim 1 +		= ,	(3.9)
lim 1 +		= ,	(3.9)
→∞

где число = 2,7182 -основание натурального логарифма.

При вычислении пределов типа (3.9) следует использовать следующие свойства:

1.lim→∞	1	+		=			(3.10)
				=
2.lim→∞	1	+	1	=			(3.11)
					=
3.lim→∞	1	+	1				(3.12)
3.lim→∞	1	+					(3.12)
			+
			1	+
4.lim→∞	1	+			=		(3.13)

Пример 3.7
						n 5	3n 1
Вычислить предел последовательности xn							.
Вычислить предел последовательности xn							.
						n 3

Решение:

Для вычисления предела преобразуем к виду (3.9). С этой целью выделим в числителе выражение, стоящее в знаменателе и почленно разделим, а затем воспользуемся свойствами (3.10)-(3.13):

		+ 5	3 +1					+ 3 + 2	3 +1
	lim				= lim				=
	lim	+ 3			= lim			+ 3	=
	→∞	+ 3				→∞		+ 3
					2		3 +1
	= lim		1 +		2			= 2∙3 = 6.
	= lim		1 +	+ 3				= 2∙3 = 6.
		→∞		+ 3
Ответ: lim→∞	+5	3 +1
Ответ: lim→∞	+3	= 6.
	+3

§ 3.4. Предел функции

Приведем два определения предела функции:

Определение 4 (по Коши). Число A называется пределом функции f x

при → , если	для любого сколь угодно малого > 0 найдется такое
0, что для						x a
0, что для	всех	x	удовлетворяющих неравенству			x a
выполняется:				f x A
					.	(3.14)
					.	(3.14)
Определение 5 (по Гейне). Число A называется пределом функции f x ,
при стремлении	x к	a ,	если какую бы последовательность			xn с

пределом a , извлеченную из множества X , ни пробегала независимая переменная x , соответствующая последовательность значений функции f x1 , f x2 , f x3 ,..., f xn ,... всегда имеет предел A .

Обозначают этот факт так:

lim f x A .	(3.15)
x a

Из определения предела функции по Гейне следует, что все теоремы о пределах последовательности можно обобщить на случай предела функции.

Далее приведем несколько примеров вычисления предела функции.

Пример 3.8


Вычислить предел функции lim				x3 1
Вычислить предел функции lim			2	3x 2
		x 1 x	2	3x 2
		Решение:
При подстановке в числитель				и	знаменатель x 1	мы получаем
	0
неопределенность типа		.
неопределенность типа		.
	0
Выделяем критический		множитель			x 1, разложив	на множители
квадратный трехчлен в знаменателе					и воспользовавшись формулой

разности кубов в числителе. Затем сократим полученное выражение на

x 1.

x 1 x 2

x 1

lim

x 3 1

lim

x 2

x 1

1 1 1

x 1 x 2 3x

2 x 1

x 1 x 2

x 1

x 2

1 2

Ответ: lim

x3 1

x 1 x2

3x 2

Пример 3.9

Вычислить предел функции

lim

x 2 x 12

x 2 4

x 3

Решение:

При подстановке			x 3 в предел мы получаем неопределенность типа
	0				2	x 12	x 3 x 4 ;
		. Числитель	разложим на множители:	x

	0

далее знаменатель и числитель нашей дроби умножим на величину сопряженную знаменателю, т.е.

x 3 x 4

x 3

x2 x 12

x 3

x 2

4 x

x 2 4 x

x 2 4 x x 2 4 x

lim

x 3 x 4

lim

x 3 x 4

lim

x 2

4 x

x 2

4 x

x 2 4 x

2 x 3

x 3

lim x 4

x 2

4 x

3 2

4 3

x 3

Ответ: lim	x2 x 12		7.

	x 2	4 x
x 3

§ 3.5. Первый замечательный предел

Первым замечательным пределом называют предел вида:

lim

sin x

(3.16)

x 0

Следствия первого замечательного предела

lim

tgx

x 0

lim

arcsin x

x 0

3. lim

arctgx

x 0

lim

sin mx

x 0

lim

sin mx

sin nx

x 0

sin x

lim

x 0

sin (mx)

lim

sin (nx)

x 0

Для пределов,	содержащих tgx, arcsin x, arctgx , справедливы	свойства,
аналогичные 4 – 7.
Определение 6.	Функция (x) называется бесконечно малой при
x a , если
	lim (x) 0	(3.17)
	x a

Определение 7. Если отношение бесконечно малых

(x)

стремится к

(x)

единице при x a :

lim

(x)

(3.18)

x a

(x)

то бесконечно малые (x)

(x)

называются эквивалентными

бесконечно малыми, и пишут

(x) ~ (x) при x a .

На основании приведенных определений

и первого замечательного

предела

(3.16)

можно

записать

следующие

соотношения

эквивалентности при

x 0 :

sin x ~ x, sin kx ~ kx, sin m x ~ xm

(3.19)

tgx ~ x, tgkx ~ kx, tg m x ~ xm

(3.20)

arcsin x ~ x, arcsinkx ~ kx, arcsinm x ~ xm

(3.21)

~ , ~ , ~

(3.22)

Пример 3.10 Вычислить предел функции

lim

1 cos x

x 2

x 0

Решение:

При подстановке x 0 имеем неопределенность типа

2 x

x 2

1 cos x

2sin

lim

2lim

x 0

4 2

2 x

x 2

Здесь мы воспользовались эквивалентностью (3.19) sin

при

x 0.

Ответ: lim

1 cos x

x 0

Пример 3.1 Вычислить предел функции

lim

tgx sin x

x 0

Решение:

При подстановке x 0 имеем неопределенность типа

tgx sin x

sin x

lim

sin x

lim

x 3

x 2

x 0

x 0 x 3

cos x

x 0

cos x

lim

1 cos x

lim

cos x

x 0 x 2

cos x

x 0 cos x x 0

x 2

Ответ: lim

tgx sin x

x 0

Пример 3.12 Вычислить предел функции

lim

tg3x

x sin 5x

Решение:

При подстановке x имеем неопределенность типа

В данном примере мы не можем применить первый замечательный предел, так как x , в подобных случаях необходимо сделать замену переменной. Причем, новая переменная должна стремиться к нулю.

tg3x

y x ;

lim

x sin 5x

x ; y 0;

y 0

lim

tg3y

lim

y 0

sin 5y

y 0

Ответ: lim

tg3x

x sin 5x

tg3 y	lim	tg 3y 3
sin 5 y
	y 0 sin 5y 5

§ 3.6. Второй замечательный предел
Вторым замечательным пределом называют предел вида:
lim 1 x 1 x e ,			(3.23)
x 0
или эквивалентное выражение
	1 x
lim 1		e .	(3.24)

x	x

Следствия второго замечательного предела

1. lim 1 kx x ek

x 0

2. lim 1 x m x em

x 0

<<< < Предыдущая 1 2 34 / 214 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в папке Математика АВАКЯН

#
15.04.20154.92 Mб40posobie1.pdf
#
15.04.2015342.22 Кб52predely_11.docx

													n
			n
lim			n				lim						n
													n

			3	10								3
n 3	3n		3					n			3n	3		10
	3n								3		3n			10
									3
											n3			n3
lim				1					1	.
								3

n		3			10				3
	3				10				3
	3					n3
						n3

													n
			n
lim			n				lim						n
													n

			3	10								3
n 3	3n		3					n			3n	3		10
	3n								3		3n			10
									3
											n3			n3
lim				1					1	.
								3

n		3			10				3
	3				10				3
	3					n3
						n3

													n
			n
lim			n				lim						n
													n

			3	10								3
n 3	3n		3					n			3n	3		10
	3n								3		3n			10
									3
											n3			n3
lim				1					1	.
								3

n		3			10				3
	3				10				3
	3					n3
						n3