
Математика АВАКЯН / posobie1
.pdfb |
|
b |
|
|
|
2) Cf x dx C f x dx |
(7.4) |
||||
a |
|
a |
|
|
|
b |
|
a |
|
|
|
3) f x dx f |
x dx |
(7.5) |
|||
a |
|
b |
|
|
|
b |
|
c |
|
b |
|
4) f x dx |
f x dx f x dx |
(7.6) |
|||
a |
|
a |
|
c |
|
5) Если f x |
0 |
x a;b и a b , то |
|
||
|
b |
|
|
|
|
|
f x dx 0 |
(7.7) |
|||
|
a |
|
|
x a;b и a b |
|
6) Если g x f x |
|
||||
|
b |
|
|
b |
|
|
g x dx f x dx |
(7.8) |
|||
|
a |
|
|
a |
|
7) Если |
m min f x , M max f x и a b , то |
|
|||
|
|
x a;b |
|
x a;b |
|
|
|
|
|
b |
|
|
m b a f x dx M b a |
(7.9) |
|||
|
|
|
|
a |
|
8) Если |
f x непрерывна на a;b , то на этом отрезке существует хотя бы |
||||
одна точка x c , |
a c b , такая, что верно равенство |
|
|||
|
b |
|
|
|
|
|
f x dx f c b a |
(7.10) |
|||
|
a |
|
|
|
|
|
|
|
|
x |
|
9) Если f x |
непрерывна и x f t dt , то имеет место равенство |
||||
|
|
|
|
a |
|
|
|
|
|
x f x |
(7.11) |
10) Если F x - |
какая-либо первообразная функции |
f x , справедливо |
|||
равенство:
|
b |
f x dx F b F a F x |
|
b |
|
|
|
|
|||
|
|
|
(7.12) |
||
|
a |
|
|
a |
|
|
|
|
|
|
|
Формула (7.12) называется формулой Ньютона-Лейбница. |
|
||||
11) Если |
f x - четная функция, то |
|
|||
|
a |
a |
|
||
|
|
f x dx 2 f x dx |
(7.13) |
||
|
a |
0 |
|
|
|
12) Если |
f x - нечетная функция, то |
|
|||
|
a |
|
|
|
|
|
f x dx 0 |
(7.14) |
|||
a
120

Геометрический смысл определенного интеграла
|
f x 0 x a;b , |
|
b |
|
|
|
|
Если |
то |
f x dx |
численно |
равен |
площади |
||
|
|
|
a |
|
функции f x , |
||
криволинейной трапеции, ограниченной сверху |
графиком |
||||||
снизу - отрезком оси 0Х, справа и слева - прямыми x a и x b . |
|
||||||
|
f x 0 x a;b , |
|
b |
|
|
|
|
|
|
|
|
|
|
||
Если |
то |
f x dx |
|
численно |
равен |
площади |
|
|
|
|
a |
|
|
|
|
криволинейной трапеции, ограниченной сверху отрезком оси 0Х, снизу - графиком функции y f x , слева и справа - прямыми x a и x b .
Вычисление определенного интеграла
b
Определенный интеграл f x dx может быть вычислен по
a
определению как предел интегральных сумм. Однако, в большинстве случаев, целесообразно воспользоваться формулой Ньютона-Лейбница
(7.12).
b
Алгоритм применения формулы (7.12) при вычислении f x dx :
a
1)Находим неопределенный интеграл f x dx .
2)Вычисляем значение полученного выражения при x b и x a .
3)Вычисляем разность полученных значений.
|
|
|
|
|
|
|
|
|
|
|
e3 |
dx |
|||
Пример 7.1. Вычислить определенный интеграл: 1 |
|
||||||||||||||
|
|
|
. |
||||||||||||
x |
|
|
|||||||||||||
1 ln x |
|||||||||||||||
Решение: |
dx |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем F x |
|
|
|
|
d |
|
ln x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 ln x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
|
|
|
||||||
1 ln x |
|
1 ln x |
|
|
|
|
|||||||||
F e3 2
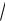 1 lne3 4
1 lne3 4
F 1 2
 1 ln1 2
1 ln1 2
Окончательно получаем:
e3 |
|
dx |
|
|
|
|
e3 |
|
|
|
|
|
|
|
|||
|
|
|
2 1 ln x |
|
4 2 2 |
|||
|
|
|
|
|
||||
x 1 ln x |
|
1 |
||||||
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
Ответ: e3 dx 2
1 x 1 ln x
1 ln x
121

При вычислении определенного интеграла применяются те же приемы, что и при нахождении неопределенного интеграла, а именно, замена переменной и метод интегрирования по частям.
Замена переменной в определенном интеграл.
Если функция y f x |
непрерывна на a;b , функция |
x t |
непрерывна вместе со своей производной и монотонна на ; , a ,b и сложная функция f t непрерывна на ; , то справедлива формула замены переменной для определенного интеграла:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
t dt |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
x dx f |
|
(7.15) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Пример 7.2. Вычислить |
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение: Сделаем замену x t 2 , тогда dx 2tdt . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Найдем пределы интегрирования для новой переменной t. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 t |
|
x 2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 9 t |
|
x 3 |
|
|
||||||||||||||||
Таким образом получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
t 2 |
|
|
|
|
|
|
|
|
3 t |
2 1 1 |
|
|
3 |
t 1 t 1 1 |
|
|||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
2tdt |
2 |
|
|
dt |
2 |
|
|
|
|
|
|
|
|
|
dt 2 |
|
|
|
|
dt |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
4 |
|
x 1 |
|
|
|
|
2 |
|
t 1 |
|
|
|
|
2 |
t 1 |
|
|
|
|
|
|
|
|
2 |
|
t 1 |
|
|
|
|
2 |
|
t 1 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
||||
–”‹‘€–’”(2.3) 2 |
|
|
t 1 dt 2 |
|
|
|
|
dt |
|
|
2 |
t |
|
t |
|
|
2 ln |
t 1 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 t |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
9 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
3 |
|
|
|
|
2 ln |
3 1 |
ln |
2 1 |
|
|
|
2 |
|
|
ln 2 7 2 ln 2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
9 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
|
|
|
|
|
|
dx 7 2 ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Метод интегрирования по частям в определенном интеграле |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Если |
функции |
u u x и v v x |
непрерывны |
вместе со своими |
|||||||||||||||||||||||||||||||||||||||||||||
производными на a;b , то имеет место формула интегрирования по частям
122

|
|
|
|
|
|
|
b |
|
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
udv uv |
vdu |
|
(7.16) |
||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
3 |
xdx |
|
|
|
|
||||
Пример 7.3. Вычислить |
|
|
|
. |
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
sin |
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx |
|
u x |
|
|
|
|
du dx |
|
|
3 |
|
||||||
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
x ctg x |
|
ctg xdx |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
4 sin |
|
x |
dv |
|
|
|
|
v ctg x |
|
4 |
4 |
|||||||
|
sin |
2 |
x |
|
||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ctg |
|
|
ctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|||||||||||||||||
|
|
|
|
3 |
|
cos xdx |
|
|
1 |
|
|
|
|
1 3 |
d |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
3 |
|
4 |
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
sin x |
|
|
|
|
|
|
3 |
3 |
|
|
|
4 |
|
4 |
|
sin x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ln |
|
sin x |
|
|
3 |
|
|
|
|
|
ln sin |
|
ln sin |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
3 |
4 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
3 |
|
|
|
3 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
ln |
3 |
|
|
ln |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
ln1,5 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||
|
3 |
3 |
|
|
|
|
|
|
|
12 |
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
|
|
|
|
3 |
|
3 4 |
ln1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
sin |
2 |
x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ 7.2. Геометрические приложения определенного интеграла |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) Вычисление площади плоской фигуры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Приложение |
|
|
определенных |
интегралов |
к |
|
|
|
вычислению площади |
|||||||||||||||||||||||||||||||||||||||||||||||||
плоской фигуры основано на геометрическом смысле определенного интеграла.
Если данная фигура ограничена двумя кривыми y f1 x |
и y f 2 |
x |
||||
и двумя |
вертикальными линиями |
x a и |
x b , причем |
f1 x f 2 |
x |
|
|
|
|
|
|
|
|
x |
a; b |
(рис. 2), то ее площадь вычисляется по формуле: |
|
|
||
|
|
b |
|
|
|
|
|
|
S f 2 |
x f1 x dx |
(7.17) |
||
Y |
a |
|
|
|
y f2 x |
|
|
y f1 x |
|
0 |
a |
b |
X |
Рис. 7.2
123
Если кривая, ограничивающая криволинейную трапецию, задана |
|||||||||||||||||||||||||||||
параметрическими уравнениями |
|
|
|
x x , |
|
|
|
|
|
y t |
, то |
площадь |
|||||||||||||||||
криволинейной трапеции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S t t dt |
|
|
|
|
|
(7.18) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a и |
|
|
|
b , |
0, t |
|
|
|||||||||||||||
где и определяются из условий |
|
|
|
|
|
|
t |
|
, |
|
. |
||||||||||||||||||
Если кривая задана в полярных координатах уравнением , то |
|||||||||||||||||||||||||||||
площадь криволинейного сектора 0M1 M2 |
(рис.3), ограниченного дугой |
||||||||||||||||||||||||||||
кривой и полярными радиусами, соответствующими углам 1 |
и 2 , |
||||||||||||||||||||||||||||
вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
d |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
S |
|
|
1 2 |
|
|
|
|
|
(7.19) |
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
Y |
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Рис. 7.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример 7.4. Вычислить площадь фигуры, ограниченной линиями |
|
|
|||||||||||||||||||||||||||
y 2 9x, |
y 3x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение: Изобразим заданную фигуру (рис.7.4) |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
y2 |
9x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
y 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.4
124
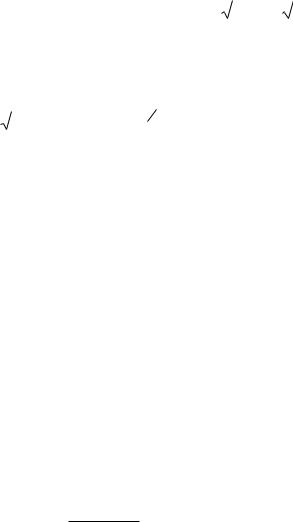
Найдем абсциссы точек пересечения заданных кривых:
y 2 9x |
3x |
2 |
9x 9x x 1 0 |
||||
|
|
||||||
y 3x |
|
|
|
|
|
|
|
x1 0, |
x2 1, |
y 9x 3 x |
|||||
Тогда площадь заштрихованной фигуры, согласно (7.17), равна:
|
1 |
|
|
3 |
|
|
3x |
2 |
|
1 |
|
|
|
|
|
|
|
|
|||||
S 3 x 3x dx 2 x |
2 |
|
|
|
|
|
|||||
|
2 |
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
|
|
S |
1 |
|
|
ед.2 |
|
|
||
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
1 |
ед.2 |
|
2 |
|
2 |
|||
|
|
|
|
||
Пример 7.5 |
Вычислить площадь фигуры, ограниченной первой |
|||
|
аркой |
циклоиды y a 1 cos t |
x a t sin t |
|
|
и осью . |
|
|
|
Решение: |
Первая арка циклоиды определяется из условия |
|||
|
y 0 |
a 1 cost 0 |
t1 0 t2 |
2 |
|
|
x t a 1 cos t |
|
|
Таким образом, площадь найдем по формуле (7.18) |
|
|||
2 |
|
|
2 |
|
S a 1 cos t a 1 cos t dt a 2 |
1 2 cos t cos2 t dt |
|||
0 |
0 |
a |
2 |
2 |
2 cos t |
|
|
|
1 |
||
|
|
0 |
|
|
3a 2 |
ед.2 |
|||
Ответ:
1 cos 2t
dt
2
S 3 a 2
a |
2 |
|
3 |
t 2 sin t |
|
|
|
|
|
||
|
|
|
|||
|
|
|
2 |
|
|
ед.2
1 |
|
2 |
|
|
sin 2t |
|
|
|
|
||
4 |
|
0 |
|
Пример 7.6. Вычислить площадь фигуры, заключенной между
первым и |
вторым витками спирали Архимеда |
|
a |
a 0 . |
|
Решение: Область между первым и вторым витками спирали |
||
соответствует 1 2 , |
2 4 . |
|
Площадь найдем по формуле (7.19):
125
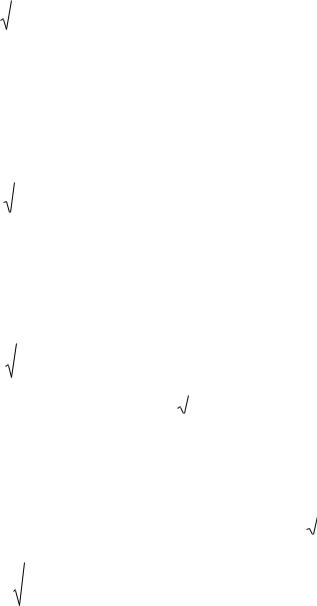
S |
1 a 2 d a |
|
|
|
2 d a |
3 |
4 |
|
|
|||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 2 |
|
|
|
|
|
|
2 2 |
|
|
|
|
2 |
|
3 |
|
2 |
|
|
||||||||
|
a 2 |
4 |
3 |
|
|
|
3 |
|
|
|
|
|
28a 2 3 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
ед. |
|
|
|
|
|
|||||||||
6 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||
Ответ: |
|
|
|
|
S |
28 |
|
3 a 2 |
ед.2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) Вычисление длины дуги кривой. |
|
|
|
|
|
|
y f x , |
|
|
|
|
f x |
|
|||||||||||||||
Пусть кривая задана уравнением |
где |
|
- непрерывно |
|||||||||||||||||||||||||
дифференцируемая |
функция, |
причем |
абсциссы |
|
точек А |
и В равны |
||||||||||||||||||||||
соответственно x a и x b . Тогда длина дуги |
|
|
|
|
может быть найдена по |
|||||||||||||||||||||||
AB |
|
|||||||||||||||||||||||||||
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 f x 2 dx |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
(7.20) |
||||||||||||
|
|
|
|
|
|
AB |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть кривая задана параметрическими уравнениями x t и y t |
||||||||||||||||||||||||||||
, где t , t - непрерывно дифференцируемые функции, причем точке А
соответствует значение t , |
|
|
|
|
|
а точке В - |
t . Тогда длина дуги AB |
||||
кривой вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
t 2 |
t 2 dt |
|
||
L |
|
(7.21) |
|||
AB |
|
|
|
|
. |
Пусть кривая задана в полярных координатах уравнением |
|||||
Причем, точке А соответствует значение 1 полярного угла, точке В - значение 2 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда длина дуги |
AB может быть найдена по формуле: |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
2 |
|
2 |
|
|
|
|
2 d |
|
|
|
(7.22) |
|
|
|||||
|
|
AB |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7.7. Вычислить длину дуги параболы y 2 |
|
|
|
|
|
|
|
||||||||||||||
|
x между |
||||||||||||||||||||
|
точками с абсциссами x1 0 и x2 |
1. |
|
|
|
|
|
||||||||||||||
Решение: Кривая задана явным уравнением, поэтому для вычисления |
|||||||||||||||||||||
длины дуги воспользуемся формулой (7.20). Вычисляем y x : |
y x |
1 |
|
. |
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
Таким образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
L |
|
|
1 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Сделаем замену t 2 1 |
1 |
|
x |
|
|
1 |
|
dx |
|
2tdt |
. |
|||
|
|
|
|
|
|
|
||||||||
|
x |
|
t |
2 |
1 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
t |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 t x 1 t 
 2
2
Таким образом
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2tdt |
|
|
|
|
|
|
|
|
b |
2t 2 dt |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L t |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
1 |
2 |
|
t |
2 |
1 |
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Найдем |
|
|
|
2t 2 dt |
|
|
, |
|
разложив |
|
|
подынтегральную |
функцию на |
||||||||||||||||||||||||||||
|
|
|
|
|
|
t 2 |
1 |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
простейшие дроби: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2t 2 dt |
|
|
|
|
2t 2 |
|
|
|
|
|
A |
|
|
A |
|
|
|
|
B |
|
|
|
|
B |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
t 1 |
|
t |
1 |
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
|
t 1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
2 |
2 |
|
|
t 1 |
|
2 |
|
|
t 1 |
|
|
2 |
|
|
|
|
||||||||||||||||||||||
|
|
t |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
2t 2 A |
|
t |
3 |
t 2 |
t 1 |
A |
t |
2 |
2t 1 |
B |
|
t 3 |
t 2 t |
1 |
B |
t 2 2t 1 |
||||||||||||||||||||||||||||
Приравнивая коэффициенты при одинаковых степенях х, получаем систему из 4-х линейных уравнений с четырьмя неизвестными:
x 3 x 2 x1 x 0
A1
A2
B1
B2
A1 B1 0 |
|
A1 A2 B1 B2 2 |
|
|
|
|
|
A1 2 A2 B1 2B2 0 |
|
A1 A2 B1 B2 0 |
|
|
|
Решая полученную систему, получаем:
21
21
21
21
127

Таким образом
|
|
2t 2 dt |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
t 1 |
2 |
t 1 |
t 1 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
t |
2 |
1 |
|
|
|
|
t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
t 1 |
|
|
|
t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
ln |
t |
1 |
|
|
|
|
|
|
|
ln |
t 1 |
|
|
|
|
|
C |
|
ln |
|
|
|
|
|
|
|
|
|
|
C |
||||||||||
|
2 |
|
t |
1 |
|
t |
|
2 |
|
t 1 |
t |
2 |
1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Воспользовавшись формулой Ньютона-Лейбница (7.12), получаем:
|
|
|
1 |
|
|
b 1 |
|
||
|
|
|
|
|
|||||
L lim |
ln |
|
|
||||||
2 |
b 1 |
||||||||
b |
|
|
|
||||||
lim |
1 |
|
|
|
|
2 |
|
||
|
|
||||||||
ln |
1 |
|
|||||||
2 |
b 1 |
||||||||
b |
|
|
|
|
|||||
Переходя к пределу при
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 |
|
|
2 1 |
2 |
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
||
b2 1 |
2 |
|
|
1 |
|
|
2 1 |
|
|||||||||
2 |
|||||||||||||||||
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|||
|
|
b |
|
|
|
|
1 |
|
|
2 |
||||||
lim |
|
|
|
2 |
ln |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
1 2 1 |
||||||||||||
b b |
1 |
|
|
|
2 |
|
||||||||||
b , окончательно получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
1 |
ln |
3 2 2 |
ед. |
|||||||
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
1 |
|
|
|
|
|
||||||||
|
L |
|
|
1 |
ln 3 2 |
|
|
|
||||||||
Ответ: |
2 |
2 |
ед. |
|||||||||||||
2 |
||||||||||||||||
Пример 7.8. Вычислить длину астроиды |
|
|||||||||||||||
|
x a cos3 t, |
y a sin3 t |
||||||||||||||
Решение: Кривая задана параметрическими уравнениями, поэтому для вычисления ее длины воспользуемся формулой (7.21)
Вычислим предварительно xt и yt :
xt 3a cos2 t sin t yt 3a sin2 t cost
Тогда, согласно (7.21), получаем, учитывая симметрию кривой:
L 4 2
 3a cos2 t sin t 2 3a sin2 t cost 2 dt
3a cos2 t sin t 2 3a sin2 t cost 2 dt
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 2 |
|
|
|
|
dt 12a 2cost sin tdt |
|
|
9a 2 cos2 t sin2 t cos2 |
t sin2 |
t |
|||
0 |
|
|
|
|
0 |
|
|
2 |
|
|
|
ед. |
|
6a sin 2tdt 3a cos2t |
2 |
6a |
||||
0 |
|
0 |
|
|
|
|
Ответ: L 6a ед.
128

Пример 7.9. Вычислить длину кардиоиды a 1 cos .
Решение: Кривая задана уравнением в полярных координатах, поэтому для вычисления ее длины воспользуемся формулой (7.22).
|
|
|
|
|
|
|
|
a sin . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Найдем |
|
|
|
a 1 cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a 2 1 cos 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
a 2 sin2 |
a 2 1 |
2 cos cos2 sin2 |
|
|
||||||||||||||||||
a 2 2 2 cos 2a 2 1 cos |
4a 2 sin |
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Подставив найденное выражение для |
|
|
|
2 в (7.22), получаем: |
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8a ед. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
L |
|
|
|
2 |
|
|
|
d 2a |
|
sin |
2 |
d 4a cos |
2 |
0 |
|
|
||||||||
|
|
|
|
0 |
|
L 8a ед. |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) Вычисление объемов тел вращения.
Пусть в пространстве задано тело, образованное вращением вокруг оси 0X криволинейной трапеции, ограниченной графиком функции y f x , прямыми x a и x b и осью 0X (рис. 7.5).
Y
0 a |
b |
|
|
Х |
|
Z |
|
|
Рис. 7.5 |
|
|
Объем этого тела можно найти по формуле: |
|
|
|
b |
|
|
V f x 2 dx |
(7.23) |
|
a |
|
Аналогично, объем тела, полученный вращением криволинейной |
||
трапеции вокруг оси 0Y , равен |
|
|
|
d |
|
|
V x y 2 dy |
(7.24) |
c
129
