
Математика АВАКЯН / posobie1
.pdf
sin2 x 1 cos 2x 2
cos2 x 1 cos 2x (6.51) 2
sin x cos x 12 sin 2x
3) m n 2k |
k N . |
В этом случае подынтегральная функция записывается в виде дроби. В знаменателе этой дроби выделяется множитель cos2 x (или
|
2 |
|
dx |
|
dx |
|
|
заменяется на d tg x |
d ctg x и |
sin |
|
x ). Выражение |
|
|
|
|
|
||
|
cos2 x |
|
|
||||||
|
|
|
sin2 |
x |
|
|
|||
делается замена tg x t .
Пример 6.15. Найти sin3 x cos2 xdx .
Решение: По условию одна из степеней нечетная, |
|
поэтому можно |
|||||||||||
записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin3 x cos2 |
xdx sin2 |
x cos2 |
x sin xdx sin2 x cos2 |
xd cos x |
|||||||||
cos x t |
|
|
|
|
|
|
1 t 2 t 2 dt t 4 |
t 2 dt |
|||||
sin2 x 1 cos2 x 1 t 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 5 |
|
t 3 |
C |
cos5 x |
|
cos3 |
x |
C |
|
|
||
|
|
|
|
|
|
|
|||||||
5 |
3 |
|
5 |
|
3 |
|
|
|
|
||||
Пример 6.16. Найти sin2 x cos2 xdx .
Решение: Преобразуем подынтегральную функцию:
sin2 x cos2 x |
1 |
sin2 |
2x , |
т.е. m 2 |
n 0 |
|
4 |
||||||
|
|
|
|
|
Применим формулу понижения степени (1.51)
14 sin2 2x 81 1 cos4x
Тогда
110

sin2 x cos2 xdx 81 1 cos 4x dx 81 dx 81 cos 4xdx 8x 321 sin 4x C
Ответ: sin 2 x cos2 xdx 8x 321 sin 4x C
Пример 6.17. Найти cos8 x dx .
Решение: m n 4 8 4, поэтому поступим согласно схеме п.3:
|
sin4 |
x |
dx |
sin4 |
x dx |
|
|
|
sin4 |
x |
d tg x tg4 |
x |
|
1 |
|
|
d tg x |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos |
8 |
x |
cos |
6 |
x cos |
2 |
x |
|
cos |
6 |
x |
cos |
2 |
x |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
tg x |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 5 |
|
|
t 7 |
|
|
|
tg5 |
x |
|
tg7 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
t 4 1 t 2 |
dt t 4 t 6 dt |
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
1 t |
2 |
|
|
|
|
|
|
|
C |
|
|
|
|
C |
|||||||||||||||||||
|
5 |
|
|
7 |
|
5 |
|
7 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
II. Интегралы вида
cos a1 x b1 cos a2 x b2 dx |
|
||||||||||
cos a1 x b1 sin a2 x b2 dx |
(6.52) |
||||||||||
sin a1 x b1 sin a2 x b2 dx |
|
||||||||||
преобразуются с помощью тригонометрических формул |
|
||||||||||
cos cos |
|
|
1 |
cos cos |
|
||||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|||||
sin sin |
1 |
|
cos cos |
(6.53) |
|||||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
sin cos |
|
1 |
sin sin |
|
|||||||
2 |
|
||||||||||
|
|
|
|
|
|
|
|
||||
Пример 6.18. Найти sin x sin |
x |
sin |
x |
dx . |
|
||||||
|
|
|
|||||||||
|
|
|
|
|
2 |
3 |
|
||||
Решение:
Преобразуем подынтегральную функцию с помощью формул
(6.53):
111
sin x sin |
x |
sin |
x |
dx sin x |
1 |
cos |
x |
cos |
5x |
|
1 |
sin x cos |
x |
|
1 |
sin x cos |
5x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
3 |
|
|
|
6 |
|
|
|
2 |
6 2 |
6 |
|
|||||||
|
2 |
|
6 |
|
|
||||||||||||||
|
1 |
sin |
7x |
sin |
5x |
|
1 |
sin |
11x |
sin |
x |
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
6 |
|
|
|
4 |
|
6 |
|
|
|
||
|
|
6 |
|
|
|
6 |
|||||||
Тогда
sin x sin |
x |
sin |
x |
dx |
1 |
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
3 |
|
|
|
4 |
|
|||||
1 |
|
6 |
|
|
7x |
|
|
6 |
|
5x |
|||||
|
|
|
cos |
|
|
|
|
|
cos |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
7 |
|
|
6 |
|
|
5 |
|
|
6 |
|
|||
|
7x |
|
5x |
|
11x |
|
x |
|
sin |
|
sin |
|
sin |
|
sin |
|
dx |
|
|
|
|
|||||
|
6 |
|
6 |
|
6 |
|
6 |
|
|
6 |
|
cos |
11x |
6cos |
x |
|
C |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
11 |
|
6 |
|
6 |
|
|
||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x sin |
x |
|
x |
|
1 |
|
6 |
|
7x |
|
6 |
|
5x |
|
6 |
|
|
11x |
|
x |
|
|
|
|
sin |
|
dx |
|
|
|
cos |
|
|
|
|
cos |
|
|
|
|
cos |
|
6 cos |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
3 |
|
4 |
|
7 |
|
|
6 5 |
|
6 11 |
|
6 |
|
6 |
|
|
|||||
III. Интегралы вида: |
tgm xdx; |
ctgm xdx , где m - целое положительное |
|||||||||||||||||||||
число, преобразующиеся с помощью тригонометрических формул:
tg2 |
|
|
1 |
|
; |
||
|
|
|
|
||||
cos2 |
1 |
||||||
|
|
|
|||||
ctg2 |
|
1 |
|
|
|
||
|
|
|
|
|
|||
sin |
2 1 |
||||||
|
|
||||||
При применении этих формул последовательно понижается степень тангенса или котангенса.
Пример 6.19. Найти tg5 xdx .
Решение:
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
3 |
xd tg x tg |
3 |
|
||||||||||
tg |
|
xdx |
tg |
|
x tg |
|
|
xdx tg |
|
x |
|
|
|
|
|
|
|
|
1 dx tg |
|
|
xdx |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
x |
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
4 |
x tg xd tg x tg xdx |
|
|
|||||||||||||||||||||||
|
|
tg |
|
x |
|
tg x |
|
|
|
|
|
|
|
1 dx |
|
|
|
|
tg |
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
tg4 x |
|
1 |
tg2 |
x |
d cos x |
|
|
1 |
tg4 x |
1 |
tg2 x ln |
|
cos x |
|
C |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
cos x |
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ: tg5 xdx |
1 |
tg4 x |
|
1 |
tg2 |
x ln |
|
cos x |
|
C |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
112

§ 6.10. Универсальная тригонометрическая подстановка
Рассмотрим интегралы вида
R cosx, sin x dx |
(6.54) |
Данный интеграл сводится к интегралу от рациональной функции аргумента t с помощью замены переменной, называемой универсальной тригонометрической подстановкой:
tg 2x t
x 2arctg x |
dx |
2dt |
|
1 t 2 |
|||
|
|
Тогда, воспользовавшись тригонометрическими формулами:
2 tg x sin x 2
1 tg2 2x
1 tg2 x cos x 2 1 tg2 2x
получаем:
|
1 t 2 |
|
|
2t |
|
|
2dt |
|
|
|
|
||
R cosx, sin x dx R |
|
|
, |
|
|
|
|
|
|
|
R1 |
t dt |
|
1 t |
2 |
|
t |
2 |
1 t |
2 |
|||||||
|
|
1 |
|
|
|
|
|
|
|||||
Пример 6.20. Найти интеграл |
|
|
|
dx |
|
|
. |
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
a cosx b sin x |
|
||||||
(6.55)
(6.56)
(6.57)
(6.58)
(6.59)
Решение: Сделаем универсальную тригонометрическую подстановку (6.57). Тогда, воспользовавшись формулами (6.56) - (6.58), получаем:
|
|
|
|
|
|
2dt |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
2dt |
|
|
|
|
|
1 t 2 |
|
|
|
|
||||
a cos x b sin x |
a |
1 t 2 |
|
b |
2t |
|
at 2 |
2bt a |
||||
|
|
|
1 t 2 |
|
1 t 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
113 |
|
|
|
|
|
|||

Разложим знаменатель полученного выражения на множители:
at 2 2bt a a t t1 t t2 , |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b2 a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где t |
1,2 |
|
|
|
|
|
- корни соответствующего квадратного уравнения. |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2dt |
|
2 |
|
|
dt |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|||||||
|
|
|
|
|
at 2 2b a |
t t |
t t |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Разложим подынтегральную функцию на простейшие |
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
A |
|
|
B |
|
A B t At2 Bt1 |
||||||||
|
|
|
|
|
|
|
|
|
t t1 t t2 |
||||||||||||
|
|
|
|
t t1 t t2 |
t t1 |
|
t t2 |
|
|||||||||||||
Приравнивая коэффициенты при одинаковых степенях t, получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A B 0 |
|
|
|
t1 |
t2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
At2 |
Bt1 1 |
B t2 t1 1 |
|
|
|
|
B |
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
t1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a 2 |
b2 |
b a 2 |
b2 |
|
|
|
|
|
|
2 a 2 |
|
b2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
1 |
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
dt |
|
|
|
|
|
|
|
2 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a t t1 t t2 a 2 |
a 2 b2 |
|
|
|
|
b |
|
a 2 b2 |
|
|
|
|
|
|
|
b |
|
|
a 2 b2 |
|
|
dt |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
b |
|
a 2 b2 |
|
|
|
|
|
|
|
|
b a 2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
ln |
t |
|
|
|
|
|
|
|
|
|
|
|
|
ln |
t |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
a |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
ln |
|
at b |
|
a 2 |
b2 |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a 2 |
b2 |
|
|
at |
b a 2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
114

|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||
Возвращаясь к исходной переменной x t tg |
|
|
|
получаем |
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
1 |
|
|
a tg |
|
b a2 b2 |
|
|
|
|||||||||
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
C |
||
a cos x b sin x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
a2 b2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
a tg |
|
b |
|
a |
2 |
b |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
1 |
|
|
a tg |
|
b a2 |
b2 |
|
|||||||
Ответ: |
|
|
|
|
ln |
2 |
C |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a cos x b sin x |
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||
a2 b2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
a tg |
|
b |
a |
|
b |
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
Следует заметить, что в случае, если подынтегральная функция |
|||||||||||||||||||
R cosx, sin x |
является |
четной |
по |
обоим аргументам, т.е. |
|||||||||||||||
R cos x, sin x R cos x,sin x , то нахождение интеграла (6.54) заметно
упрощается, если вместо замены (6.55) сделать подстановку |
|
tg x t |
(6.60) |
dx
Пример 6.21. Найти 4 cos2 x 5sin2 x .
Решение: Подынтегральная функция является четной по обоим аргументам:
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
4 cosx 2 5 sin x 2 |
|
4 cos2 x 5sin2 x |
||||
Сделаем замену: t tg x . Тогда |
x arctgt |
dx |
dt |
||||
|
. |
||||||
1 t 2 |
|||||||
Используя тригонометрические функции, получаем:
sin2 |
x |
|
|
tg2 x |
|
|
|
|
t 2 |
|
|
|
tg2 x |
|
|
t 2 |
|
||||
|
1 |
1 |
|
|||||||
cos2 |
x |
|
1 |
|
|
|
1 |
|
||
|
|
|
|
|
|
|||||
|
tg2 x |
|
t 2 |
|
||||||
|
1 |
1 |
|
|||||||
Подставляем sin2 x, cos2 x, dx в искомый интеграл:
115

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
1 |
|
|
|
dt |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|||||||||||
4 cos |
x 5sin |
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5t |
3 |
9t |
3 |
|
|
3 t |
||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
3t C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
arctg |
|
|
arctg |
3 arctg x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
3 |
3 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
arctg x C |
|
|
|
|
|
|||||||||||||||||||
Ответ: |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||||
4 cos |
2 |
x |
5sin |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Задания для cамостоятельного решения
Задание 6.1. Найти интегралы и сделать проверку.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
6.2 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
6.3 |
|
4 5x3 |
x 3 |
|
x x2 |
dx |
||||||||||||||||||
6.1 |
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|||||||||
|
2 5x 2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
||||||||||||||||
6.4 |
|
|
|
2 |
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
6.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
6.6 |
|
|
|
|
|
|
|
|
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||
6.7 |
ex |
32 x dx |
6.8 |
|
|
|
x2 |
|
4 |
|
dx |
|
|
|
|
|
6.9 |
|
|
x2 |
|
dx |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3x |
2 |
|
3 |
|
|
|
|
|
4 |
x |
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
6.10 |
|
|
|
|
|
|
6.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6.12 tg x ctg x dx |
|
||||||||||||||||||||||||
x |
4 |
x |
2 |
|
sin |
2 |
x cos |
2 |
x |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Задание 6.2. Найти интегралы, используя метод занесения под знак дифференциала.
6.13 |
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
cos xdx |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 x |
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
dx |
|
|
|
|||||||||||||
|
|
|
|
|
|
6.14 |
|
|
|
|
|
|
|
|
|
|
|
|
6.15 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 sin x 3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x3 3 |
|
||||||||||||||||||||||||||||
6.16 |
|
|
|
sin 2xdx |
6.17 |
|
|
|
xdx |
|
|
|
|
|
|
|
6.18 |
|
|
|
xdx |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 sin |
2 |
x |
|
4 x |
2 |
|
|
|
|
|
|
|
4 x |
4 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
5x dx |
|
|
|
|
|
|
|
|
|
|
|
5x dx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
6.19 |
|
|
|
|
|
|
|
|
|
|
6.20 |
|
|
|
6.21 |
|
|
cos |
|
x |
dx |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
5x |
1 |
|
|
|
|
|
|
|
|
|
|
25x |
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln x3 |
1 2 |
|
|||||||||||||||||||
6.22 |
|
|
|
|
|
|
|
|
|
arctg |
|
|
x |
6.24 |
|
|||||||||||||||||||||||||||||
|
|
6.23 |
|
|
|
|
|
dx |
|
|
|
|
|
dx |
||||||||||||||||||||||||||||||
x 2 ln x 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 x |
|
|
|
|
x3 1 |
||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Задание 6.3. Найти интегралы, используя формулу интегрирования по частям.
6.25 |
ln 5xdx |
6.26 |
2x sin x cos xdx |
6.27 |
arccosxdx |
|
6.28 |
x2 1 sin xdx |
6.29 |
3x2 |
5 e2 x dx |
6.30 |
x2 arctgxdx |
|
|
|
|
116 |
|
|

6.31 |
e2 x cosxdx |
|
|
|
|
|
6.32 |
|
cos ln x dx |
||||||||||||||||||||
6.34 |
|
sin |
|
|
|
|
|
|
|
|
|
|
x5ex2 dx |
|
|
|
|||||||||||||
|
|
|
xdx |
|
|
|
|
|
6.35 |
|
|
|
|||||||||||||||||
Задание 6.4. Найти интегралы. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6.37 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
6.38 |
|
|
|
|
dx |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
2x |
3 |
|
|
|
|
|
x |
2 |
10x 25 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6.40 |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
6.41 |
|
|
|
|
xdx |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2x |
2 |
|
2x 3 |
|
x |
2 |
6x 5 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6.43 |
|
|
|
|
|
|
|
x 3 |
|
|
|
|
dx |
6.44 |
|
|
|
ex dx |
|
|
|
||||||||
x 2 |
2x 3 |
|
|
||||||||||||||||||||||||||
e2 x 7ex |
12 |
||||||||||||||||||||||||||||
6.46 |
|
|
|
|
|
|
4x 3 5x |
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
4 |
|
2x |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Указания:
6.33ln 3 x dx
x2
6.36 |
|
arcsin x |
|
dx |
|
|
|
||
|
|
1 x2 3 |
||
dx
6.39 x 2 4x 8
6.42 |
|
|
|
|
xdx |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
2x |
2 |
2x 5 |
||||||||||
|
|
|
|
|||||||||
6.45 |
|
|
2x3 3x |
|
|
dx |
||||||
|
x |
4 |
x |
2 |
|
1 |
||||||
|
|
|
|
|
|
|
||||||
взадании 6.44 воспользоваться подстановкой ex t ;
взаданиях 6.45 и 6.46 воспользоваться подстановкой x 2 t .
Задание 6.5. Найти интегралы.
6.47 |
|
|
|
3x 2 3x 12 |
dx |
6.48 |
|
|
|
x 2 dx |
|
|
|
|
|
|
|
|
|
|
6.49 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
x |
2 |
|
|
|
|
|
|
|
|||||||||||
|
|
x |
3 |
x |
2 |
|
2x |
1 |
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
6.50 |
|
|
|
|
|
|
x 8 dx |
|
|
|
|
6.51 |
|
|
|
|
|
x 4 1 dx |
6.52 |
|
x4 6x3 12x2 6 dx |
|||||||||||||||||||||||||||||||||||||||||
x 3 4x 2 |
|
|
4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 6x2 12x 8 |
|||||||||||||||||||||||||||||||||||||
|
x 3 x 2 |
|
x 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
6.53 |
|
|
x 1 2 dx |
|
|
|
|
6.54 |
|
|
|
|
|
|
|
xdx |
|
|
|
|
|
6.55 |
|
|
|
|
|
x 2 dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6x |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
x2 1 2 |
|
|
|
|
|
x |
|
|
|
x 1 |
5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Указание: в задании 6.54 |
воспользоваться |
подстановкой |
x 2 3 t , в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
задании 6.55 |
x 1 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Задание 6.7. Найти интегралы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
6.66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6.67 |
|
|
|
|
x |
|
|
dx |
6.68 |
|
|
|
|
|
|
|
|
|
|
dx |
||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 x 2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 x 2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 3 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
6.69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
x 6 x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
117 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

Задание 6.8. Найти интегралы.
6.71 |
|
|
|
|
cos3 xdx |
|
|
6.72 sin5 x cos2 3 |
xdx |
|
|
|
6.73 sin4 xdx |
||||||||||||||||||||||||||||
6.74 |
|
|
|
|
|
|
|
dx |
|
|
|
|
6.75 |
|
|
|
|
|
|
dx |
|
|
|
|
dx |
|
|
|
6.76 |
|
|
cos2x cos6xdx |
|||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
sin |
|
x cos x |
|
|
|
|
|
|
sin x cos7 x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
6.77 |
|
|
|
sin 3x cos5xdx |
|
|
6.78 |
cos x cos |
x |
cos |
x |
dx |
6.79 |
|
|
tg4 xdx |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.80 |
|
|
ctg6 xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Задание 6.9. Найти интегралы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6.81 |
|
|
|
dx |
|
|
|
|
|
|
|
6.82 |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
6.83 |
|
|
|
|
dx |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
sin |
3 |
x |
|
|
|
|
|
sin x cos x |
|
|
|
|
5 3cos x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6.84 |
|
|
|
|
|
|
|
|
|
dx |
|
|
6.85 |
|
|
|
|
dx |
|
|
|
6.86 |
|
|
|
dx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8 |
|
4sin x 7cos x |
|
9 |
8cos x sin x |
sin |
2 |
x 5sin x cos x |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
6.87 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
6.88 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
5 cos |
2 |
x 9 sin |
2 |
x |
|
sin |
2 |
x 2 sin x cos x 5cos |
2 |
x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
VII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 7.1. Понятие определенного интеграла. Свойства определенного интеграла
Пусть |
на отрезке |
|
a;b |
|
задана функция |
y f |
|
x |
|
. |
Разобьем отрезок |
||||
|
|
|
|
||||||||||||
a;b произвольным образом |
точками a x0 |
x1 |
x2 |
xn |
b на n |
||||||||||
частичных |
отрезков длиной |
xi |
xi |
xi 1 . |
Выберем |
внутри |
каждого |
||||||||
частичного отрезка точку i : xi 1 |
i |
xi |
(рис.7.1.). |
|
Найдем |
значение |
|||||||||
функции y f x в точках i . |
|
|
|
|
|
|
|
|
|
|
|
||||
118
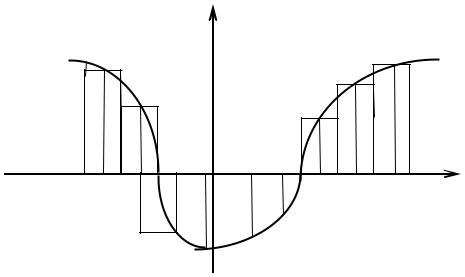
Y
A B
3 4 0
|
|
|
|
|
|
|
|
|
a 1 x1 2 |
x2 |
|
|
|
n-1 xn-1 n b |
X |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.1
Интегральной суммой функции |
y |
|
|
|
|
на отрезке |
|
|
называется |
f |
|
x |
|
a;b |
|
||||
сумма вида: |
|
|
|
|
|
|
|
|
|
|
n |
|
|
i xi |
|
|
|
||
Sn |
f |
|
|
(7.1) |
|||||
i 1
Геометрически Sn представляет собой алгебраическую сумму
площадей прямоугольников, в основаниях которых лежат частичные отрезкиxi , а высоты равны f i (рис. 7.1).
Определение: Определенным интегралом от функции f x на отрезке
|
|
|
|
|
a;b |
|
называется предел интегральной суммы (7.1), найденный при условии, |
||
что длина наибольшего из частичных отрезков стремится к нулю: |
|
|||
|
|
n |
b |
|
|
|
lim f i xi |
f x dx |
(7.2) |
|
|
max xi 0 i 1 |
a |
|
Справедлива следующая теорема:
Если функция y f x непрерывна на отрезке a;b , то она интегрируема на a;b ; т.е. предел интегральной суммы (7.1) существует и не зависит от способа разбиения отрезка a;b .
Свойства определенного интеграла:
b |
b |
b |
|
1) f x g x dx f x dx g x dx |
(7.3) |
||
a |
a |
a |
|
|
|
119 |
|
