Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский Государственный Технический Университет им. П.О. Сухого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика АВАКЯН / posobie1

.pdf

Скачиваний:

Добавлен:

15.04.2015

Размер:

4.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

§6.3. Метод замены переменной в неопределенном интеграле

Метод замены переменной заключается в том, что в интеграле

f x dx , нахождение которого затруднительно, вводят новую

переменную t, связанную с прежней переменной соотношением

x t	(6.13)
	(6.13)
dx t dt
При этом соотношение (6.13) подбирают таким образом, чтобы
полученный интеграл f1 t dt стал табличным или,	по крайней мере,

был бы ясен способ его нахождения. После вычисления f1 t dt следует

вернуться к исходной переменной, используя соотношение (1.13) или обратное к нему.

Следует помнить, что функция t в (1.13) должна быть строго

монотонной, имеющей непрерывную первую производную функцией переменной t на некотором промежутке изменения аргумента t.

Найти

Пример 6.3.

Решение: Ведем новую переменную t:

x ln t .

Тогда

x ln t

ex 1

e ln t

t 1

d t 1

табличный интеграл II ln

t 1

C t e x

t 1

C ln

C x ln

ex 1

e x 1

ex 1

Ответ:

x ln

ex 1

Следует заметить, что часто удобно вводить не замену переменной

по формуле (6.13), а делать замену вида

t x

(6.14)

При этом для нахождения dx необходимо выразить x через t и далее действовать согласно приведенной выше схеме.

Пример 6.4. Найти xdxx 1 .

Решение: Для вычисления данного интеграла необходимо ввести новую переменную таким образом, чтобы избавиться от иррациональности в подынтегральной функции. Поэтому вводим новую переменную

x 1,

тогда x t 2

1, dx 2tdt .

Таким образом:

xdx

1 2tdt

t 2 1 dt 2 t

C 2t t 2

3 C

x 1

2 x 1

x 1 3

2 x 1

x 2 C

xdx

x 1 x

2 C

Ответ:

x 1

Тригонометрические и гиперболические подстановки.

Часто для вычисления интегралов, содержащих радикалы вида

a2 x2 ,

применяются

тригонометрические

гиперболические подстановки.

1)Если интеграл содержит a2 x 2 , то во многих случаях нахождение его существенно упрощается заменой:

x asin t

(6.15)

Пример 6.5.

Найти

x2 dx

Решение: Сделаем тригонометрическую

подстановку

x asin t ,

тогда

x2 dx

x a sin t

a2 sin 2 ta costdt

sin 2 t costdt

a2 x2

a2 sin 2 t

a 1 sin 2 t

dx a costdt

a2 sin 2 t costdt a2 sin 2 tdt cost

Для вычисления полученного интеграла воспользуемся формулой понижения степени:

sin2 t 1 cos2t 2

Тогда

	2	2	2	1 cos2t		a2			a2		1
				2		2			2		2
a		sin tdt a			dt		dt	cos2tdt		t		sin2t	C

Для того, чтобы вернуться к исходной переменной, необходимо провести следующие преобразования:

12 sin 2t 12 2sin t cost sin t 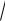1 sin 2 t .

Учитывая, что x asin t ;

sin t

;

1 sin 2 t

a2 x2 ;

t arcsin ax , окончательно получаем:

x2 dx

arcsin

a2 x2

a 2

x2 dx

Ответ:

a2 x2 C

arcsin

a2 x2

2) Если интеграл содержит радикал

x2 a2 , то полагают

(6.16)

cost

Следует отметить, что часто,

полученный в результате указанной

подстановки интеграл, в свою очередь, оказывается довольно сложным. В таком случае можно вместо подстановки (6.16) воспользоваться

гиперболической подстановкой
x acht	(6.17)

При использовании гиперболических подстановок надлежит помнить, что

	ch2 t sh2t 1			(6.18)
	sht		cht	(6.19)
cht		sht

3) Интеграл, содержащий радикал 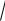x2 a2 может быть упрощен путем замен

x a tgt	(6.20)
или
x asht	(6.21)

	§ 6.4. Метод интегрирования по частям
	Метод интегрирования по частям основан на применении
формулы
	udv u v vdu	(6.22)
где	u x и v x - непрерывно дифференцируемые на	некотором
интервале функции.
	Формула (6.22), называемая формулой интегрирования по частям,

позволяет перейти от более сложного интеграла udv к более простому

vdu .

Кинтегралам, которые находят методом интегрирования по частям, относятся интегралы следующих видов:

1) Pn x cos xdx, Pn x sin xdx , где Pn x - полином n-ой степени от x.
В данном случае за u x следует выбрать Pn x , а за dv x - cos xdx
или sin xdx .
				Pn 1 x dx -					полином степени на
Тогда du Pn x dx Pn 1 x dx,				Pn 1 x dx -					полином степени на
единицу меньшей, чем исходный.
Таким образом,	u Pn x								x dx
	u Pn x				du Pn 1				x dx
Pn x cos xdx
Pn x cos xdx	dv cos xdx				v		1	sin xdx
	dv cos xdx				v			sin xdx


=		1	Pn x sin x		1	Pn 1 x cos xdx
=			Pn x sin x			Pn 1 x cos xdx

Таким образом, в результате применения формулы (6.22) мы пришли к интегралу более простому по отношению к исходному. Следует подчеркнуть, что формула интегрирования по частям может быть применена несколько раз, до тех пор, пока мы не придем к P0 x ,

т.е. не придем к интегралу sin xdx или cos xdx .

2)Pn x e x dx , где Pn x - полином степени n от x.

Вданном случае за u x обозначают Pn x , за dv x - e x dx . Формула интегрирования по частям применяется до тех пор, пока не останется e x dx .

3) Pn x ln xdx;	Pn x arctgxdx;	Pn x arcsin xdx
		93

В данном случае за u x следует выбирать ln x ; arctgx ; arcsin x , за dv x - Pn x dx .

Тогда du	1	dx,	du	1		dx, du	dx	dx, v P	x и в результате

	x			1 x2	1		x2	n 1

применения формулы интегрирования по частям мы приходим к интегралам, содержащим только рациональные функции и радикалы.

4) Интегралы вида sin xeax dx, cos xebx dx вычисляются с помощью

двукратного применения формулы интегрирования по частям и последующего решения полученного уравнения относительно исходного интеграла. Следует отметить, что в данном случае безразлично, что изначально принимать за u x , а что за dv x .

		Пример 6.6. Найти x2											3x 2 cos3xdx
														Решение
												2		3x 2
x2								u x						3x 2			du 2x 3 dx
x2		3x 2 cos 3xdx																1
								dv cos 3xdx									v	1		sin 3x
								dv cos 3xdx									v			sin 3x
																	3
																	u				1		2x 3					du		2		dx
					1									1			u						2x 3					du				dx
x2		3x 2			1		2x 3							1					3										3
						sin 3x									sin 3xdx				3										3
					3	sin 3x								3	sin 3xdx																1
					3									3																	1
																	dv sin 3xdx											v					cos 3x
																															3
1	x		2	3x 2 sin 3x						1									1							2
											2x		3 cos 3x									cos 3x					dx
											2x		3 cos 3x									cos 3x					dx
3										9									3							3
1	x2			3x 2 sin 3x				1	2x 3 cos 3x							2	cos 3xdx							1	x2			3x 2 sin 3x
	x2			3x 2 sin 3x					2x 3 cos 3x								cos 3xdx								x2			3x 2 sin 3x
3							9								9									3

19 2x 3 cos 3x 272 sin 3x C 271 9x2 27 x 18 2 sin 3x

19 2x 3 cos 3x C 271 9x2 27 x 20 sin 3x 19 2x 3 cos 3x C

Ответ:

x2 3x 2 cos 3xdx 271 9x2 27 x 20 sin 3x 19 2x 3 cos 3x C

Пример 6.7. Найти x arctgxdx .

Решение:

																								dx																		x	2
							u arctgx										du																2											dx
																							x	2								x
																								2																2
																										1														2
	x arctgxdx																																	arctgx -
	x arctgxdx																				x2													arctgx -						x2
																					x2											2								x2				1
							dv xdx										v
																						2
		x2			1					x2 dx
				arctgx
		2		arctgx			2			x2			1
	Для				вычисления												полученного																	интеграла,												преобразуем
подынтегральную функцию:
								x2						x2 1 1									x2		1								1		1					1

						x2 1									x2 1								x2		1						x2 1									x2 1
						x2 1									x2 1								x2		1						x2 1									x2 1
Таким образом,
		x2						1			x2dx						x2												1									1
				arctg x															arctg x													1									dx
	2			arctg x				2			x		2	1			2		arctg x										2			1				x	2				dx
	2							2			x			1			2												2							x				1
			x2						1		dx					1			dx								x2												1				1
					arctg x																									arctg x										x					arctg x C
			2		arctg x				2							2		x	2		1					2				arctg x									2	x			2		arctg x C
			2						2							2		x			1					2													2				2
Ответ: x arctg xdx											x2			arctg x						1			x			1		arctg x C .
Ответ: x arctg xdx														arctg x						2			x			2		arctg x C .
												2								2						2

§ 6.5. Интегрирование выражений, содержащих квадратный трехчлен

Вычисление интегралов вида

I		dx	(6.23)

	x2	px q
	x2	px q

состоит в сведении данного интеграла к одному из табличных интегралов вида I, II или VII в зависимости от соотношения коэффициентов p и q.

Возможны следующие случаи:

I.p2 4q 0

Вэтом случае квадратный трехчлен имеет два действительных

корня

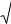
					x1,2		p			p2	4q			(6.24)
					x1,2				2					(6.24)
и x2 px q x x		x x		.					2
и x2 px q x x		x x	2	.
1			2
Подынтегральную функцию в (6.23) можно преобразовать
следующим образом:
		1				1					A	B		(6.25)

	x2 px q				x x	x x		2			x x	x x	2
				1				2			1		2

Числа А и В должны быть подобраны таким образом, чтобы выражение (6.25) было тождеством.

Чтобы найти А и В приведем правую часть равенства (6.25) к общему знаменателю

	A	B		A x x2 B x x1
	x x	x x	2	x x x x	2
1			2	1	2
Приравняем числитель полученной дроби к 1.
		A x x2 B x x1 1				(6.26)

Т.к. выражение должно быть тождественным (т.е. справедливым для всех х) приравняем коэффициенты при одинаковых степенях х в обеих частях (6.26)

x1 :	A B 0
x0 :		1
x0 :	Ax2 Bx1	1
	Решая полученную систему, получаем
		A		1		B			1

			x	x	2		x	2	x
		1			2			2	1

Таким образом, получаем

dx			1	dx			1	dx

x2 px q	x	2	x	x x	x	2	x	x x	2
		2	1	1		2	1		2

Полученные интегралы - табличные типа II, поэтому получаем

	dx			1	ln	x x2	C	(6.27)
x2	px q	x	2	x	ln	x x	C	(6.27)
			2	1	1

где x1,2 - корни квадратного трехчлена, входящего в искомый интеграл.

II. p2 4q 0

		2				p 2
В этом случае	x		px q	x			и искомый	интеграл

						2
представляет собой табличный интеграл типа I с 2.
Таким образом, в случае p2			4q .
			dx			1	C	(6.28)

	x 2		px q		x p 2

III.p2 4q 0

Вданном случае квадратный трехчлен не имеет действительных корней. Преобразуем его, выделив полный квадрат:

p 2

4q p2

px q x

q x

p2 4q 0 , то

4q p2

т.к.

a 2

0, поэтому

d x

{согласно (6.4}

px q

{табличный интеграл VII }

arctg

Таким образом, в случае p2 4q 0

arctg

2x p

(6.29)

x 2

px q

4q p2

Пример 6.8.

Найти

Решение:

Найдем p2 4q 25 4 6 1 0.

Найдем корни	x1,2		5 1	x1 3;		x2 2, поэтому
			2

			dx			dx

		x 2 5x 6			x 3 x 2

Разложим подынтегральную функцию на простые дроби:

1	A	B	A x 2 B x 3

x 3 x 2	x 3	x 2	x 3 x 2

Приравняем числитель полученной дроби числителю исходной:

A x 2 B x 2 1

Приравняем коэффициенты при одинаковых степенях х:

x 1 : A B 0

x 0 : 2A 3B 1

Решаем данную систему:

A 1 B 1

Таким образом:

x 2 5x 6

x 3

x 2

x 3

C ln

Ответ:			dx		x 2
				ln		C
	x	2	5x 6		x 3

Для вычисления интеграла вида

mx n

I x 2 px q dx

необходимо выделить производную знаменателя подынтегральной функции:

x 2 px q 2x p

(6.30)

вчислителе

mx n m2 2x p mp2 n

Тогда интеграл (6.30) преобразуется в сумму двух интегралов

	m		2x p
I				dx n
I		x 2	px q	dx n
	2	x 2	px q

mp		dx	I		I 2
						(6.31)
	x 2	px q		1
2

Интеграл I1 найдем методом занесения

под

знак дифференциала

2x p dx d x 2 px q ,

интеграл I 2 найдем

по одной из формул

(6.27)-(6.29) в зависимости от соотношения коэффициентов p и q .

Таким образом,

mx n

px q

(6.32)

x2 px q

Пример 6.9. Найти

3x 2

dx .

2x 4 в

Решение:

Найдем

x 2 4x 5

4. Выделим

числителе

подынтегральной

функции:

3x 2

2x 4 6 2

2x 4 4 .

Таким образом

3x 2

2x 4

I1 4I 2

x 2 4x 5

2x 4

x 2

x 2 4x

x 2

4x 5

x 2 4x 5

{табличный

интеграл

4x 5

4 1

типа VII} arctg x 2 C2

Ответ:

3x 2

4x 5

4 arctg x 2 C

4x 5

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в папке Математика АВАКЯН

#
15.04.20154.92 Mб40posobie1.pdf
#
15.04.2015342.22 Кб52predely_11.docx