БДЗ №1
по специальным разделам математического анализа
Выполнил:
Студент группы МП-26
Пузырев Д. В.
Проверил:
Хахалин С. Я.
Оценка:____________________________
Подпись преподавателя:____________________________
Задание 1: Найти все Лорановские разложения функции F(z)
а).
По степеням z.
б). По степеням (z+1)
а). Аналитичность функции нарушается в точках z=0 и z=-1.
Разложим функцию методом неопределенных коэффициентов:
Тогда коэффициенты равны соответственно
А=1; B=-1; C=-2;
Функция примет вид:
Заметим, что:
, тогда, сделав замену, получим:
1/z – уже является разложением в ряд Лорана по степеням z, а два последних являются суммами геометрических прогрессий:
Тогда разложения функции по степеням z в области аналитичности будут представлены в виде:
б). Введем замену переменной: z+1=t
Тогда, подставив в функцию, получим:
Разложим функцию методом неопределенных коэффициентов:
Тогда коэффициенты равны соответственно:
A=-1; B=1; C=-1;
Функция примет вид:
Но, 1/t2 и 1/t уже являются разложениями в ряд Лорана по степеням t (По степеням (z+1)) , а последнее представляется в виде суммы геометрической прогрессии:
Задание 2: Разложить функцию F(z) в ряд Лорана в окрестности z0.
Введем замену переменной: (z+i/3)=t
Тогда, подставив в функцию, получим:
Преобразуем ее так, что бы разложить по степеням t:
Подставив, получим:
Задание 3: Выяснить характер особых точек функции F(z)
а).
Представим
функцию в виде
Она имеет особые точки +i, -i, 1,
∞- не является особой точкой, т.к. функция после подстановки z=1/t примет вид
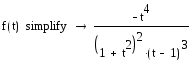
Определение 1: Функция f(z) называется аналитической функцией в области g, если она дифференцируемая во всех точках zg и ее производная непрерывна в этой области
Определение 2: Точка z называется изолированной особой точкой функции f(z), если f(z) – однозначная аналитическая функция в кольце 0<|z-z0|<R, a z0 – особая точка.
Исследуем функцию F(z) на Аналитичность:
Найдем
ее производную:
Ее непрерывность нарушается только в особых точках: +i,-i, 1 и предел во всех точках кроме этих равен ее значению.
Значит функция аналитична на всей плоскости, кроме этих точек.
Значит точки +i, -i, 1 - изолированные особые точки.
Теперь найдем предел функции в каждой из этих точек:
Значит точка z0=1 является существенно особой, т.к. предел в ней не существует, а точки z0=±i – полюсы порядка m.
Найдем порядок полюсов ±i:
Особая точка является Полюсом порядка m≥1, если для функции g(z)=1/f(z) точка z0 является нулем порядка m, т.е. g(z) имеет вид g(z)=(z-z0)m φ(z), φ(z0)≠0;
Т.е. Это полюсы второго порядка.
б). Функция
имеет две особые точки: z0=0 и z0=∞;
Проверим функцию F(z) на аналитичность, для этого найдем ее производную и проверим ее непрерывность.
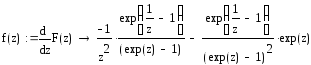
Она непрерывна во всех точках, кроме z0=0;
Значит точки z0=0 и z0=∞ являются изолированными особыми точками.
Теперь найдем предел функции в каждой из этих точек, что бы выяснить их характер.
З
начит
точка z0=∞ является
устранимой особой точкой, а точка z0=0
– существенно особая точка.
Задание 4: Найти вычеты функций F(z) относительно всех изолированных особых точек.
a). Сначала разложим знаменатель на множители, для этого решим уравнение:
Тогда функция примет вид:
Как мы видим существует 4 особые точки, их выясним характер.
Для выяснения изолированности найдем производную от F(z), и проверим ее на непрерывность. Если она непрерывна, то функция аналитична, а если функция аналитична в кольце 0<|z0-z|<R, то точки изолированы.
Как мы видим производная имеет особенности только в 4 особых точках нашей функции, значит все эти точки – изолированы.
Выясним их характер, для этого найдем пределы функции при z, стремящемся к z0:
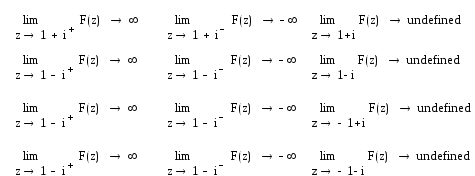
То, что пределов функции в этих точках не существует, означает, что эти точки существенно особые.
Мы знаем, что вычет функции совпадает с коэффициентом c-1 Лорановского разложения по степеням z-z0, т.е.
Найдем разложения в ряд Лорана в каждой из этих точек:
Как мы видим, коэффициенты с-1 равны соответственно:
т.е. вычеты равны:
Отдельно исследуем характер точки ∞:
Проверим особая ли она, для чего разложим ее в ряд Лорана в z0=∞.
Для этого введем замену переменных:
Тогда функция примет вид:
Она не имеет особенности в точке 0, т.е. ∞ - правильная точка.
б).
В данном случае существует две особые точки 0 и ∞.
Исследуем их характер:
Сначала выясним изолированные ли они, для этого надо узнать существует ли кольцо вокруг каждой из точек, в котором функция аналитична. Продифференцируем ее:
ее непрерывность нарушается только в точке 0, значит обе точки изолированы.
Выясним их характер, для этого найдем предел функции в этих точках.
Значит обе эти точки устранимые.
По второй теореме о вычетах, сумма вычетов этой функции равна 0, значит достаточно найти только один из них.
Тогда вычет в точке ∞ отличается от предыдущего только знаком.
Задание 5: Вычислить интегралы, используя теорию вычетов.
а).
Т.е. для вычисления этого интеграла надо вычислить вычеты во всех изолированных особых точках.
Функция имеет 3 особые точки, точка ∞ таковой не является.
Это точки ±1 и 3.
Проверим изолированные ли они, для чего найдем производную функции и проверим ее на непрерывность (Проверка функции на аналитичность):
Непрерывность этой производной нарушается только в точках ±1 и 3.
Т.е. Все три особые точки изолированы.
Найдем характер этих точек, для чего отыщем предел функции в этих точках.
Значит все эти точки – полюсы порядка m.
Найдем порядок каждого из полюсов, для этого представим функцию g(z)=1/f(z) в виде g(z)=(z-z0)m φ(z), φ(z0)≠0;
Это значит, что все эти три особые точки – полюсы второго порядка.
Для полюса второго порядка Вычет находиться по формуле:
Найдем вычеты:
Тогда искомый интеграл будет находиться по формуле:
б).
Известно, что интегралы вида:
Подынтегральная функция симметрична относительно оси OY, следовательно наш интеграл будет равен половине интеграла от -∞ до ∞
Н
айдем
особые точки нашей функции:
Это точки ±i.
Точка ∞ не является особой, это видно, если сделать замену z=1/t. Тогда функция примет вид:
Теперь видно, что функция не имеет особой точки в t=0 (x=∞).
Выясним изолированность особых точек, для этого проверим функцию на аналитичность:
Производная функции равна:
Как можно заметить ее непрерывность нарушается только в точках ±i, а значит вокруг каждой из этих точек существует кольцо 0<|z-z0|<r где функция аналитична. Т.е. Это изолированные точки.
Теперь выясним характер этих точек, для чего найдем пределы функции в этих точках:
Т
.к.
пределы существуют и равны ∞, то эти
точки – полюсы порядка m.
Найдем порядки этих полюсов, для этого
представим функцию g(z)=1/f(z)
в виде g(z)=(z-z0)m
φ(z),
φ(z0)≠0;
Значит обе эти точки – полюсы второго порядка.
Для полюса второго порядка Вычет находиться по формуле:
Найдем вычеты:
Только точка i лежит в верхней полуплоскости, поэтому искомый интеграл будет равен:
в).
Сделав замену переменных, получим:
Можно заметить, что у подынтегральной функции всего две особые точки -1/2 и -2. Точка ∞ не является особой, это видно, если сделать замену z=1/t. Тогда функция примет вид:
Т
еперь
видно, что функция не имеет особой точки
в t=0 (z=∞).
Выясним изолированность особых точек, для этого проверим функцию на аналитичность:
Производная функции равна:
Как можно заметить ее непрерывность нарушается только в точках -1/2 и -2, а значит, вокруг каждой из этих точек существует кольцо
0<|z-z0|<r где функция аналитична. Т.е. Это изолированные точки.
Теперь выясним характер этих точек, для чего найдем пределы функции в этих точках:
Т
.к.
пределы существуют и равны ∞, то эти
точки – полюсы порядка m.
Найдем порядки этих полюсов, для этого
представим функцию g(z)=1/f(z)
в виде g(z)=(z-z0)m
φ(z),
φ(z0)≠0;
Значит обе эти точки – полюсы второго порядка.
Для полюса второго порядка Вычет находиться по формуле:
Найдем вычеты:
Значит искомый интеграл равен:
